
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторные операции II-го порядка.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте СИМВОЛИКА ГАМИЛЬТОНА.
В предыдущих параграфах мы ввели понятия: вектора Пусть 1)
Где 2) 3) Известным английским математиком Гамильтоном было замечено, что все эти (и многие другие) операции можно записать кратко при помощи следующего символического вектора – оператора
Проекции символического вектора оператора Гамильтона – суть.
Сам вектор Тогда символически (обращаясь с 1) Таким образом, под символическим произведением вектора
2) 3) Найдем векторное произведение символического вектора:
= Производную по направлению можно записать в виде:
Таким образом, операции первого порядка могут быть единообразно записаны с помощью символического вектора набла.
УТВЕРЖДЕНИЕ. Векторные операции I-го порядка линейны относительно своих аргументов. Доказательство: Следует из линейности дифференцирования и скалярного и векторных произведений. НАПРИМЕР.
Заметим также, что соотношения, содержащие Многие формулы векторного анализа легко выводятся при использовании символического вектора Применяя, оператор 1. Если оператор 2. Чтобы отметить тот факт, что 3. Все величины, на которые оператор Так, например, в функции одной переменной и тогда правило нахождения производной произведения сводится:
ЗАМЕЧАНИЕ. Под дифференциальными операциями II-го порядка понимаются операции, в которых символ Усвоим некоторые элементы техники обращения с оператором Вы можете проверить получающиеся формулы в координатах. 1) Пусть
2) 3) = 4) = Наряду с обозначениями векторного произведения Нами будет использовано и двойное векторное произведение, известное вам из аналитической геометрии (1 семестр):
5) = 6) = 7) Вектор 8) Т.к. векторы 9) 10) Наряду с Df. Оператором Лапласа или Лапласианом называется закон образования дивергенции от вектора
Справедлива формула:
Df. Скалярное поле Дифференциальные операции II-го порядка можно для наглядности записать в виде таблицы:
ТАБЛИЦА ОСНОВНЫХ ВЕЛИЧИН ПОЛЯ
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 517; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 , характеризующего скорость изменения скалярного поля; производную по направлению
, характеризующего скорость изменения скалярного поля; производную по направлению  , характеризующую скорость изменения величины
, характеризующую скорость изменения величины 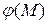 в направлении l; скаляра
в направлении l; скаляра  , вектора
, вектора  , характеризующих плотность источников и вращательную способность векторного поля. Были указаны формулы для вычисления этих величин в декартовых координатах.
, характеризующих плотность источников и вращательную способность векторного поля. Были указаны формулы для вычисления этих величин в декартовых координатах.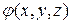 - скалярное поле,
- скалярное поле,  - векторное поле.
- векторное поле.

 - единичный вектор в направлении
- единичный вектор в направлении  .
. - скаляр.
- скаляр. - вихрь вектора
- вихрь вектора  , являющийся вектором.
, являющийся вектором. (читается «набла», оператор Гамильтона).
(читается «набла», оператор Гамильтона).
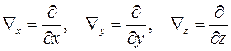 .
. ) операции 1), 2), 3) которые называют операциями I-го порядка можно записать в виде:
) операции 1), 2), 3) которые называют операциями I-го порядка можно записать в виде:

 с координатами:
с координатами:

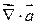
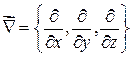 на вектор
на вектор  - есть вектор.
- есть вектор.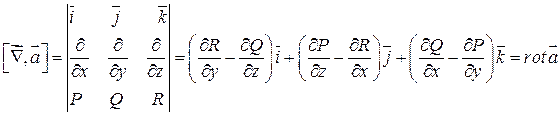


 =
=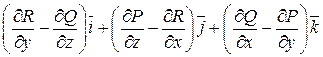 - это вектор, который называют вихрем поля
- это вектор, который называют вихрем поля 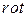 от английского слова
от английского слова  - вращение.
- вращение. и вообще
и вообще  .
.
 и
и 

 ).
). или «стрелкой» (например
или «стрелкой» (например  ), который в окончательном результате может быть снят.
), который в окончательном результате может быть снят. оператор
оператор 
 , тогда
, тогда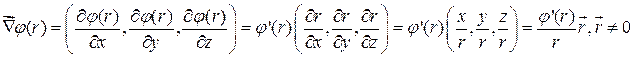




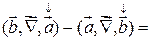

 будем использовать и
будем использовать и  .
.

 .
.
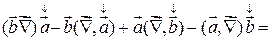
 .
. .
. поэтому скалярное произведение равно 0, т.е.
поэтому скалярное произведение равно 0, т.е.  . Т.е. поле вихря вектора
. Т.е. поле вихря вектора 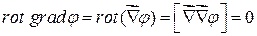 .
. .
.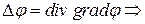 физический смысл. Численное значение Лапласиана определяет плотность источников (если
физический смысл. Численное значение Лапласиана определяет плотность источников (если  ) или стоков (если
) или стоков (если  ) векторного поля
) векторного поля  , где символ
, где символ  , так что
, так что  .
. , удовлетворяющее условию
, удовлетворяющее условию  , называется лапласовым или гармоническим полем.
, называется лапласовым или гармоническим полем.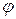













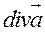 ;
;
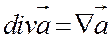

 П
П
 ;
в частности через замкнутую поверхность S:
;
в частности через замкнутую поверхность S:
 (Теорема
Остроградского)
(Теорема
Остроградского)





 ;
;
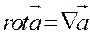
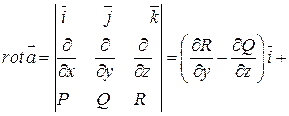 +
+ 
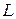 ;
W
;
W
 где
где

 .
.

 +
+ 
 вдоль контура l.
Ц
вдоль контура l.
Ц
 .
.


 +
+
+
+  .
.

 +
+  +
+  .
.



