
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 12. Элементы теории поверхностей.Содержание книги
Поиск на нашем сайте ГЛАВА 12. ЭЛЕМЕНТЫ ТЕОРИИ ПОВЕРХНОСТЕЙ. Раннее мы встречались с поверхностями, задаваемыми либо в явном виде z=f(x,y), либо в неявном виде F(x,y,z)=0. Рассмотрим более общий случай задания поверхности. Df.1 Пусть Поверхностью П в пространстве
U y x Df.2 Пусть П задана
Уравнение (1) эквивалентно трем уравнениям:
Более сокращенно
Также определяются производные высших порядков Пусть
Матрица Якоби отображение Df.3 П называется гладкой, если Но А, В, С – миноры матриц второго порядка.
Тогда Если зафиксировать
При фиксированном
Линии (6) и (7) образуют два семейства линий на поверхности П. (Сравним с отображением плоских областей).
Как известно касательные вектора к этим линиям в точке К линии Для касательной плоскости – эти вектора направляющие
НАПРИМЕР.
П 0 D x
Кроме гладких поверхностей будем рассматривать кусочно-гладкие. Df.4 П – называется кусочно-гладкой поверхностью, если можно разбить на конечное число гладких поверхностей. Причем эти части имеют общими только куски границы.
ОРИЕНТАЦИЯ ПОВЕРХНОСТИ. Остановимся на понятии ориентированной поверхности. Пусть
x y Тогда Внешней стороной поверхности П назовем ту сторону, которая соответствует положительному направлению вектора Противоположная сторона – внутренняя, она соответствует вектору « Если на поверхности можно выбрать внешнюю и внутреннюю стороны, то она называется двусторонней. Выбрать сторону Существуют неориентированные (не двусторонние) поверхности. ПРИМЕР.Лист Мебиуса (немецкий математик 1790-1868 год). Если склеить прямоугольник так, чтобы А совпала с В’, а В совпала с А’, получится поверхность, называемая листом Мебиуса. При обходе по листу Мебиуса нормаль меняет направление на противоположное.
А А’
У двусторонней поверхности Для двусторонней поверхности можно согласовать сторону поверхности с направлением обхода любого замкнутого контура Пусть
Если система координат (U,V) – правая, то при обходе В частности при z=z(x,y).
y
x Т.е. внешней соответствует сторона, у которой можно так выбрать ориентацию (сторону) ее гладких кусков, что общие части ориентации кусков обходятся в разных направлениях.
ФОРМУЛА СТОКСА. Df.1 Пусть
(1) операторная форма записи
Очевидно, операция Th.1 (ТЕОРЕМА СТОКСА) Пусть
(3) – формула Стокса. (Б/д).
При этом сторона поверхности и направление обхода контура Th.2 (ТЕОРЕМА ГРИНА) Пусть
(4) – формула Грина. (Б/д). Покажем, что (4) – есть частный случай формулы Стокса. Причем это нельзя считать доказательством, т.к. при доказательстве (3) используется (4). Итак: плоскость П зададим так:
D=П
Тогда
Из (3)
Здесь
СЛЕДСТВИЕ ИЗ Th.1 Пусть
Рассмотрим Пусть D – поверхность: Г – граница (кусочно-гладкая) поверхности D. Направление обхода D согласовано с
где
Отметим, что Перейдем в (*) к пределу при
Т.к. СЛЕДСТВИЕ 2. Пусть САМОСТОЯТЕЛЬНО. Действительно
СИМВОЛИКА ГАМИЛЬТОНА.
В предыдущих параграфах мы ввели понятия: вектора Пусть 1)
Где 2) 3) Известным английским математиком Гамильтоном было замечено, что все эти (и многие другие) операции можно записать кратко при помощи следующего символического вектора – оператора
Проекции символического вектора оператора Гамильтона – суть.
Сам вектор Тогда символически (обращаясь с 1) Таким образом, под символическим произведением вектора
2) 3) Найдем векторное произведение символического вектора:
= Производную по направлению можно записать в виде:
Таким образом, операции первого порядка могут быть единообразно записаны с помощью символического вектора набла.
УТВЕРЖДЕНИЕ. Векторные операции I-го порядка линейны относительно своих аргументов. Доказательство: Следует из линейности дифференцирования и скалярного и векторных произведений. НАПРИМЕР.
Заметим также, что соотношения, содержащие Многие формулы векторного анализа легко выводятся при использовании символического вектора Применяя, оператор 1. Если оператор 2. Чтобы отметить тот факт, что 3. Все величины, на которые оператор Так, например, в функции одной переменной и тогда правило нахождения производной произведения сводится:
ЗАМЕЧАНИЕ. Под дифференциальными операциями II-го порядка понимаются операции, в которых символ Усвоим некоторые элементы техники обращения с оператором Вы можете проверить получающиеся формулы в координатах. 1) Пусть
2) 3) = 4) = Наряду с обозначениями векторного произведения Нами будет использовано и двойное векторное произведение, известное вам из аналитической геометрии (1 семестр):
5) = 6) = 7) Вектор 8) Т.к. векторы 9) 10) Наряду с Df. Оператором Лапласа или Лапласианом называется закон образования дивергенции от вектора
Справедлива формула:
Df. Скалярное поле Дифференциальные операции II-го порядка можно для наглядности записать в виде таблицы:
ТАБЛИЦА ОСНОВНЫХ ВЕЛИЧИН ПОЛЯ
ГЛАВА 12. ЭЛЕМЕНТЫ ТЕОРИИ ПОВЕРХНОСТЕЙ. Раннее мы встречались с поверхностями, задаваемыми либо в явном виде z=f(x,y), либо в неявном виде F(x,y,z)=0. Рассмотрим более общий случай задания поверхности. Df.1 Пусть Поверхностью П в пространстве
U y x Df.2 Пусть П задана
Уравнение (1) эквивалентно трем уравнениям:
Более сокращенно
Также определяются производные высших порядков Пусть
Матрица Якоби отображение Df.3 П называется гладкой, если Но А, В, С – миноры матриц второго порядка.
Тогда Если зафиксировать
При фиксированном
Линии (6) и (7) образуют два семейства линий на поверхности П. (Сравним с отображением плоских областей).
Как известно касательные вектора к этим линиям в точке К линии Для касательной плоскости – эти вектора направляющие
НАПРИМЕР. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 - область,
- область,  - замыкание области.
- замыкание области. непрерывное отображение области
непрерывное отображение области  :
:
 V z П
V z П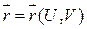 ….. (1),
….. (1), 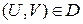 . Тогда
. Тогда  поверхность класса
поверхность класса  , если
, если  имеет в области
имеет в области  или
или  ;
;  .
. (2)
(2) . Уравнения (1) и (2) называются параметризацией поверхности П. Напомним, что под производными
. Уравнения (1) и (2) называются параметризацией поверхности П. Напомним, что под производными 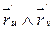 понимаются вектора:
понимаются вектора: (3)
(3)

 , где
, где  .
. . Составим матрицу Якоби.
. Составим матрицу Якоби.
 (4)
(4) .
. и
и 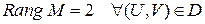 . Т.к.
. Т.к.  линейная независимость строк
линейная независимость строк  не коллинеарны, т.е.
не коллинеарны, т.е.  .
. (5)
(5)
 . Рассмотрим точку
. Рассмотрим точку  , причем
, причем  .
. , то получим параметрическое уравнение линии:
, то получим параметрическое уравнение линии: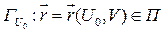 (6)
(6) , получаем линию:
, получаем линию: (7)
(7) V
V 


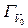
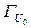




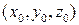 получены следующим образом: к линии
получены следующим образом: к линии 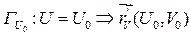

 нормальный вектор:
нормальный вектор: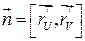 (8)
(8) ,
, 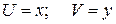

 (9)
(9)
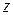









 z
z 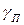

 D П
D П



 .
. .
. задать ориентацию (ориентировать) поверхности.
задать ориентацию (ориентировать) поверхности. В В’
В В’
 при обходе замкнутого контура вектор
при обходе замкнутого контура вектор  .
. .
. z
z 
 -острый,
-острый, 
 . Очевидно,
. Очевидно,  граница П. П называется двусторонней, если она удовлетворяет следующим условиям:
граница П. П называется двусторонней, если она удовлетворяет следующим условиям:
 ,
,  - область, векторное поле
- область, векторное поле 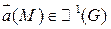 . Ротором (вихрем) векторного поля
. Ротором (вихрем) векторного поля  называется:
называется: (1)
(1) . Для того, чтобы получить обычную запись необходимо рассмотреть определитель. При этом нужно понимать:
. Для того, чтобы получить обычную запись необходимо рассмотреть определитель. При этом нужно понимать: и т.д. Тогда:
и т.д. Тогда:
 векторное поле
векторное поле 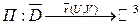 - кусочно-гладкая;
- кусочно-гладкая;  - кусочно-замкнутый контур, ограничивающий П. Тогда:
- кусочно-замкнутый контур, ограничивающий П. Тогда: (3)
(3)













 - область,
- область,  , тогда:
, тогда: (4)
(4) .
.
 .
.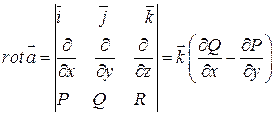
 (по теореме о сведении поверхностного интеграла II-го рода к двойному)
(по теореме о сведении поверхностного интеграла II-го рода к двойному) , очевидно
, очевидно  , т.е. С=1. Итак:
, т.е. С=1. Итак:
 , G -область,
, G -область,  определен в G и инвариантен относительно системы координат.
определен в G и инвариантен относительно системы координат. Доказательство:
Доказательство:



 Г
Г

 D ● ●
D ● ●  G
G П
П направление, задаваемое
направление, задаваемое  .
.
 =
=  ,
,  - проекция
- проекция  , что
, что (*)
(*)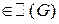 - непрерывное векторное поле.
- непрерывное векторное поле. (
(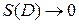 ,
,  ). В силу непрерывности
). В силу непрерывности 
 и
и  не зависят от выбора системы координат, то
не зависят от выбора системы координат, то 
 и считать, что
и считать, что  , проекции
, проекции  . Есть его координаты).
. Есть его координаты). (т.е.
(т.е.  и они непрерывны в G)
и они непрерывны в G)  определяет соленоидальное поле в G, т.е.
определяет соленоидальное поле в G, т.е.  .
. .
.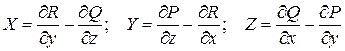 :
:  .
. , характеризующего скорость изменения скалярного поля; производную по направлению
, характеризующего скорость изменения скалярного поля; производную по направлению  , характеризующую скорость изменения величины
, характеризующую скорость изменения величины 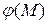 в направлении l; скаляра
в направлении l; скаляра  , вектора
, вектора 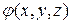 - скалярное поле,
- скалярное поле,  - векторное поле.
- векторное поле.

 - единичный вектор в направлении
- единичный вектор в направлении  .
. - скаляр.
- скаляр. - вихрь вектора
- вихрь вектора  (читается «набла», оператор Гамильтона).
(читается «набла», оператор Гамильтона).
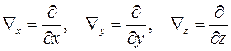 .
. ) операции 1), 2), 3) которые называют операциями I-го порядка можно записать в виде:
) операции 1), 2), 3) которые называют операциями I-го порядка можно записать в виде:

 с координатами:
с координатами:

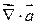
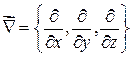 на вектор
на вектор  - есть вектор.
- есть вектор.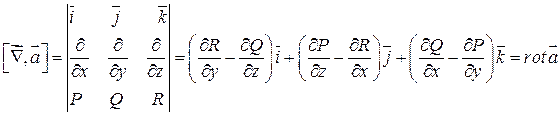


 =
=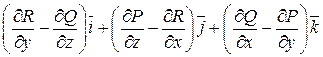 - это вектор, который называют вихрем поля
- это вектор, который называют вихрем поля 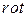 от английского слова
от английского слова  - вращение.
- вращение. и вообще
и вообще  .
.
 и
и 

 ).
). или «стрелкой» (например
или «стрелкой» (например  ), который в окончательном результате может быть снят.
), который в окончательном результате может быть снят. оператор
оператор 
 , тогда
, тогда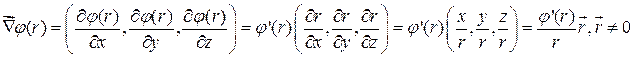




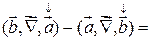

 будем использовать и
будем использовать и  .
.

 .
.
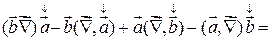
 .
. .
. поэтому скалярное произведение равно 0, т.е.
поэтому скалярное произведение равно 0, т.е.  . Т.е. поле вихря вектора
. Т.е. поле вихря вектора 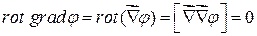 .
. .
.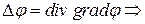 физический смысл. Численное значение Лапласиана определяет плотность источников (если
физический смысл. Численное значение Лапласиана определяет плотность источников (если  ) или стоков (если
) или стоков (если  ) векторного поля
) векторного поля  , где символ
, где символ  , так что
, так что  .
. , удовлетворяющее условию
, удовлетворяющее условию  , называется лапласовым или гармоническим полем.
, называется лапласовым или гармоническим полем.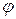













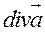 ;
;
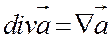

 П
П
 ;
в частности через замкнутую поверхность S:
;
в частности через замкнутую поверхность S:
 (Теорема
Остроградского)
(Теорема
Остроградского)





 ;
;
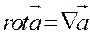
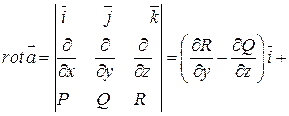 +
+ 
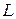 ;
W
;
W
 где
где

 .
.

 +
+ 
 вдоль контура l.
Ц
вдоль контура l.
Ц
 .
.


 +
+
+
+  .
.

 +
+  +
+  .
.



