
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула Остроградского – Гаусса.Содержание книги Поиск на нашем сайте
Пусть В декартовой системе координат Df.1 Df.2 Дивергенцией (расходимостью) векторного поля
Отметим, что операция Дивергенция в заданной точке характеризует мощность источников и стоков в данной точке. Те точки, где
Абсолютная величина дивергенции характеризует производительность (интенсивность) источников и стоков. Если Th.1 (ОСТРОГРАДСКОГО - ГАУССА) Пусть область и и и
Тогда справедлива формула Остроградского – Гаусса:
* Причем, поверхностный интеграл берется по внешней стороне поверхности.
Доказательство: Скалярный вид формулы Остроградского – Гаусса:
Пусть в G z - цилиндроид, т.е.:
Тогда: Докажем формулу:
Пусть теперь G является также и
Суммируя (4), (5) и (6) получим (3):
В векторной форме (3) имеет вид Интеграл от дивергенции векторного поля Пусть теперь G – объединение областей указанного типа:
Заметим, что теорема Остроградского – Гаусса справедлива для областей более общего вида. СЛЕДСТВИЕ.
Доказательство:
По теореме о среднем для кратных интегралов:
Отметим, что
Перейдем в (***) к
Т.к. поток
Из (7) Таким образом Df.2 Пусть Th.2 (НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ УСЛОВИЕ СОЛЕНОИДАЛЬНОСТИ ПОЛЯ Пусть G – область, для которой возможно применение формулы Остроградского – Гаусса. Доказательство: Необходимость: Пусть
Достаточность: Пусть
ФОРМУЛА СТОКСА. Df.1 Пусть
(1) операторная форма записи
Очевидно, операция Th.1 (ТЕОРЕМА СТОКСА) Пусть
(3) – формула Стокса. (Б/д).
При этом сторона поверхности и направление обхода контура Th.2 (ТЕОРЕМА ГРИНА) Пусть
(4) – формула Грина. (Б/д). Покажем, что (4) – есть частный случай формулы Стокса. Причем это нельзя считать доказательством, т.к. при доказательстве (3) используется (4). Итак: плоскость П зададим так:
D=П
Тогда
Из (3)
Здесь
СЛЕДСТВИЕ ИЗ Th.1 Пусть
Рассмотрим Пусть D – поверхность: Г – граница (кусочно-гладкая) поверхности D. Направление обхода D согласовано с
где
Отметим, что Перейдем в (*) к пределу при
Т.к. СЛЕДСТВИЕ 2. Пусть САМОСТОЯТЕЛЬНО. Действительно
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 504; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.114.140 (0.008 с.) |

 - область. В G задано векторное поле
- область. В G задано векторное поле 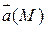 .
.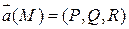 .
.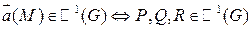 , т.е. существуют все частные производные
, т.е. существуют все частные производные 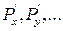 и они непрерывны в G.
и они непрерывны в G.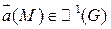 в точке M(x,y,z) называется скаляр:
в точке M(x,y,z) называется скаляр: (1)
(1) ставит в соответствие векторному полю
ставит в соответствие векторному полю  скалярное поле
скалярное поле 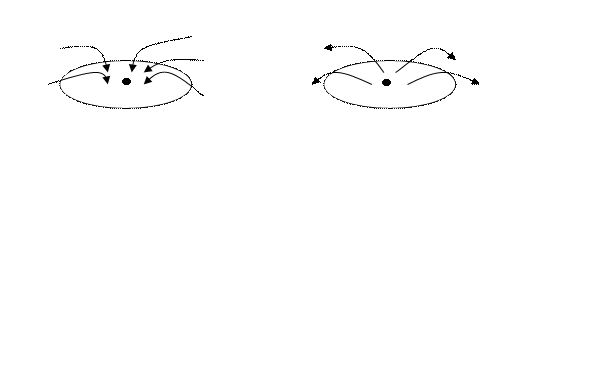
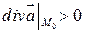
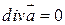 , то в точке М нет ни источника, ни стока.
, то в точке М нет ни источника, ни стока. можно представить в виде объединения конечного числа областей
можно представить в виде объединения конечного числа областей 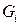 , каждая из которых является одновременно:
, каждая из которых является одновременно: -цилиндром,
-цилиндром, - цилиндром,
- цилиндром,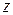 -цилиндром,
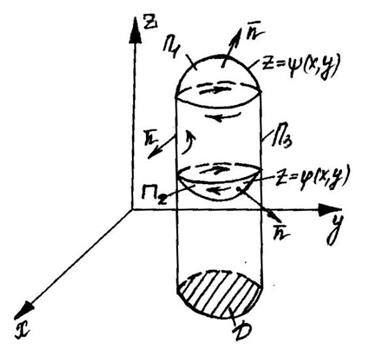
-цилиндром,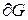 - кусочно-замкнутая гладкая поверхность, ограничивающая G. После
- кусочно-замкнутая гладкая поверхность, ограничивающая G. После 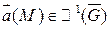 .
.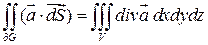 (2)
(2)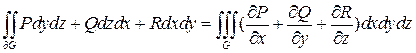 (3)
(3)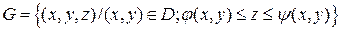 .
.
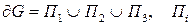 -гладкие.
-гладкие.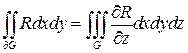 (4)
(4)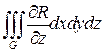 =
=  (по теореме 5 и формуле (9))=
(по теореме 5 и формуле (9))= 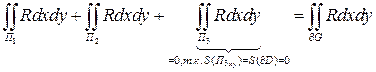 .
.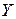 -цилиндроидом. Тогда аналогично можно показать, что:
-цилиндроидом. Тогда аналогично можно показать, что: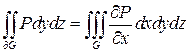 (5)
(5)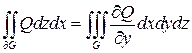 (6)
(6)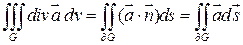
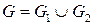 .
.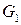 П
П


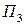
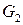
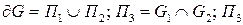 - гладкая.
- гладкая. 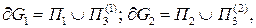 тогда:
тогда: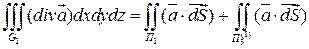 (*)
(*)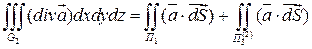 (**)
(**)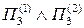 - две стороны одной поверхности (с нормалями
- две стороны одной поверхности (с нормалями 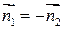 ). Отсюда скалывая, получим:
). Отсюда скалывая, получим: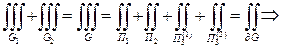 формула (2).
формула (2).


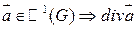 инвариантен относительно системы координат, т.е. не зависит от выбора системы координат.
инвариантен относительно системы координат, т.е. не зависит от выбора системы координат.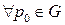 . Пусть
. Пусть 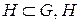 - открытая область, для которой верна теорема Остроградского – Гаусса.
- открытая область, для которой верна теорема Остроградского – Гаусса. 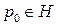 ,
, 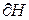 - замкнутая поверхность. ограничивающая H. Тогда:
- замкнутая поверхность. ограничивающая H. Тогда: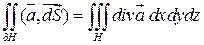
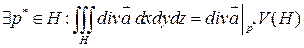 .
.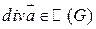 , т.к.
, т.к. 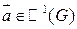 .
.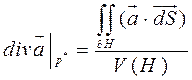 (***)
(***) при
при 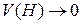 . В силу непрерывности
. В силу непрерывности 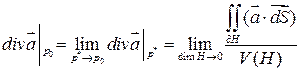 (7)
(7)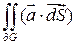 и
и 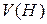 не зависят от системы координат
не зависят от системы координат 
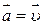 - скорость жидкости.
- скорость жидкости. 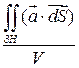 - средняя объемная плотность потока жидкости через поверхность
- средняя объемная плотность потока жидкости через поверхность 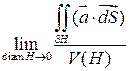 - плотность источника в точке
- плотность источника в точке  .
.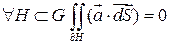 .
.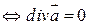 в G.
в G.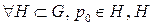 - область допускающая применение формулы Остроградского – Гаусса. Тогда по (7):
- область допускающая применение формулы Остроградского – Гаусса. Тогда по (7):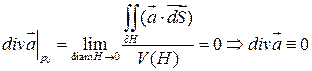 в G.
в G.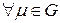 . Пусть
. Пусть 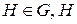 - допускает применение формулы Остроградского – Гаусса, по ней:
- допускает применение формулы Остроградского – Гаусса, по ней: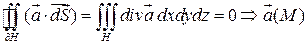 соленоидальное.
соленоидальное. называется:
называется: (1)
(1) . Для того, чтобы получить обычную запись необходимо рассмотреть определитель. При этом нужно понимать:
. Для того, чтобы получить обычную запись необходимо рассмотреть определитель. При этом нужно понимать: и т.д. Тогда:
и т.д. Тогда:
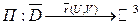 - кусочно-гладкая;
- кусочно-гладкая;  - кусочно-замкнутый контур, ограничивающий П. Тогда:
- кусочно-замкнутый контур, ограничивающий П. Тогда: (3)
(3)



















 - область,
- область,  - кусочно-гладкая граница D, ориентированная против часовой стрелки;
- кусочно-гладкая граница D, ориентированная против часовой стрелки;  , тогда:
, тогда: (4)
(4) .
.
 , кроме того
, кроме того  .
.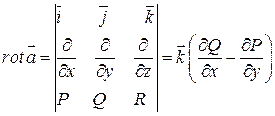
 (по теореме о сведении поверхностного интеграла II-го рода к двойному)
(по теореме о сведении поверхностного интеграла II-го рода к двойному) , очевидно
, очевидно  , т.е. С=1. Итак:
, т.е. С=1. Итак:
 определен в G и инвариантен относительно системы координат.
определен в G и инвариантен относительно системы координат. Доказательство:
Доказательство:



 Г
Г

 D ● ●
D ● ●  G
G П
П направление, задаваемое
направление, задаваемое  .
.
 =
=  ,
,  - проекция
- проекция  , что
, что (*)
(*) - непрерывное векторное поле.
- непрерывное векторное поле. (
(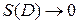 ,
,  ). В силу непрерывности
). В силу непрерывности 
 и
и  не зависят от выбора системы координат, то
не зависят от выбора системы координат, то 
 и считать, что
и считать, что  , проекции
, проекции  . Есть его координаты).
. Есть его координаты). (т.е.
(т.е.  и они непрерывны в G)
и они непрерывны в G)  определяет соленоидальное поле в G, т.е.
определяет соленоидальное поле в G, т.е.  .
. .
.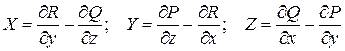 :
:  .
.


