
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поверхностный интеграл II –го рода.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Df.1 Пусть
Поверхностным интегралом от вектора-функции
Если рассматривать интеграл по внутренней стороне поверхности, то:
В дальнейшем, если нет особых говорок, под интегралом по поверхности П будем понимать интеграл по внешней стороне В прямоугольной декартовой системе координат Тогда:
это выражение зависит не только от вектора-функции P,Q,R, но и от направления нормали в каждой точке этой поверхности. Т.к.
Обозначим Т.к. dS – бесконечно малый элемент площади поверхности, то выражения
Т.е.
В правой части формулы (5) достаточно запомнить написанное слагаемое
R Q dz dy Следует помнить, что не допускается в «символах» типа dxdy перестановки. Последний интеграл называется поверхностным интегралом II-рода по выбранной стороне поверхности. По сути дела – это координатная форма записи поверхностного интеграла от вектор - функции. (5) можно рассматривать как сумму трех интегралов, которые также носят название поверхностных интегралов II- рода и обозначаются так:
Отметим, что формулы (4) и (6) дают фактически связь поверхностного интеграла II-го рода с поверхностным интегралом I-го рода. ЗАМЕЧАНИЕ. Отличие поверхностного интеграла II-го рода от интеграла I-го рода состоит в том, что в интеграле II-го рода элемент площади dS рассматривается не как скалярная величина, а как вектор
Df.2 Пусть
Перейдем к условиям существования поверхностного интеграла II-го рода. Th.1 (НЕОБХОДИМОЕ УСЛОВИЕ) Пусть (Б/д).
Th.2 (ДОСТАТОЧНОЕ УСЛОВИЕ) Пусть (Б/д). Th.3 (СВЕДЕНИЕ ПОВЕРХНОСТНОГО ИНТЕГРАЛА II-ГО РОДА К ДВОЙНОМУ) Пусть
= Доказательство:
Учитывая, что ЗАМЕЧАНИЕ. Если учесть, что
При помощи двойного интеграла по плоской области D, от смешанного произведения трех векторов
+ При получении формулы (8’) было применено разложение определителя третьего порядка по элементам первой строки; определители второго порядка записаны через соответствующие Якобианы. При переходе от левой части к правой в (8’) нужно произвести следующие замены символов:
СЛЕДСТВИЕ. Пусть
Доказательство: Следует из формулы (8) и того факта, что Заметим, что в следствии предполагается, что П проектируется на область Th.5 Пусть П может быть задана любым из трех способов:
где
Причем знак «+» берется в том случае, если Доказательство: Покажем справедливость последней формулы в (10). Остальные доказываются аналогично, нужно только выписать формулы для координат вектора
= ЗАМЕЧАНИЕ 1. В этом случае. Если используются формулы (9) или (10) и нет взаимнооднозначных проекций на координатные плоскости необходимо ЗАМЕЧАНИЕ 2. Если:
Т.е. П – цилиндрическая поверхность. Доказательство этого факта следует из определения поверхностного интеграла II-го рода и того факта, что в этих случаях соответственно:
СВОЙСТВА ПОВЕРХНОСТНОГО ИНТГЕРАЛА II-ГО РОДА Поверхностные интегралы II-го рода обладают теми же свойствами, что и поверхностные интегралы I-го рода, кроме того и дополнительными свойствами. Полагаем, что П – гладкая ориентированная, I. Линейность. (Переформулировать самостоятельно.) Аналогично как и для поверхностного интеграла II-го рода, принимая II. При перемене стороны поверхности поверхностный интеграл изменяет свой знак.
Где Доказательство:
III. Пусть П – гладкая,
Доказательство следует из связи поверхностного интеграла II-го рода с поверхностным интегралом I-го рода и определения последнего через интегральные суммы. Аналогично:
где
где
где
ПРИЛОЖЕНИЕ ПОВЕРХНОСТНОГО ИНТЕГРАЛА II-ГО РОДА Пусть П – поверхность,
Положим, что на
Поэтому Если поток < 0, то это значит, что жидкость вытекает. Df.1 Потоком векторного поля
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 454; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.45.223 (0.006 с.) |

 - простая (без самопересечений) гладкая ориентированная поверхность.
- простая (без самопересечений) гладкая ориентированная поверхность. 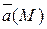 - определена на П,
- определена на П,  .
.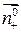 - единичный вектор нормали к поверхности П, соответствует внешней стороне.
- единичный вектор нормали к поверхности П, соответствует внешней стороне.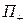 называется поверхностный интеграл I-го рода от функции
называется поверхностный интеграл I-го рода от функции 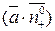 ;
;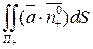 (1)
(1)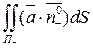 (2)
(2)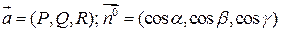 .Очевидно:
.Очевидно: 
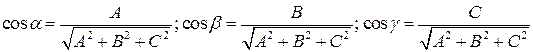
 (3)
(3) - проекция вектора
- проекция вектора  на направления нормали
на направления нормали  , то:
, то: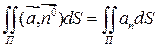 (4)
(4)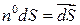 - вектор, соответствующий элементу поверхности dS.
- вектор, соответствующий элементу поверхности dS.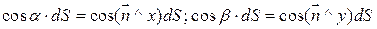 ;
;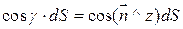 - представляют собой проекции элемента dS на плоскости yz, zx, xy.
- представляют собой проекции элемента dS на плоскости yz, zx, xy.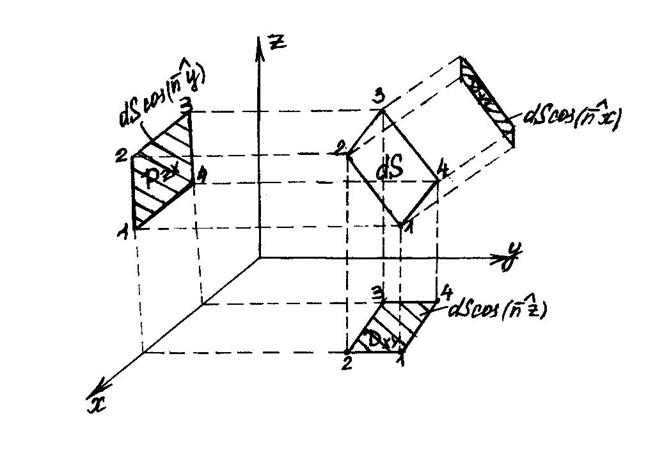
 - координаты этого вектора есть проекции
- координаты этого вектора есть проекции 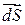 на координатные плоскости. Тогда:
на координатные плоскости. Тогда: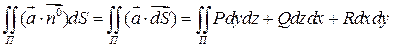 (5)
(5)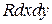 , т.к. остальные слагаемые получаются при помощи круговой подстановки символов.
, т.к. остальные слагаемые получаются при помощи круговой подстановки символов. P dx
P dx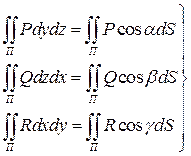 (6)
(6)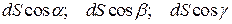
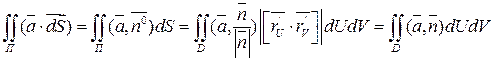 (*)
(*)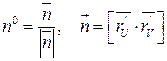
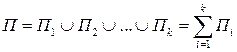 -ориентированная кусочно-гладкая поверхность, тогда поверхностным интегралом от векторной функции называется:
-ориентированная кусочно-гладкая поверхность, тогда поверхностным интегралом от векторной функции называется: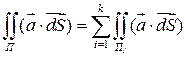 (7)
(7)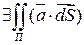 и П кусочно-гладкая
и П кусочно-гладкая 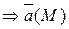 ограничена на П.
ограничена на П.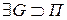 , что
, что  . П кусочно-гладкая
. П кусочно-гладкая 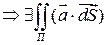 .
.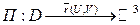 - гладкая ориентированная и
- гладкая ориентированная и 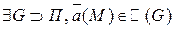 . Тогда:
. Тогда: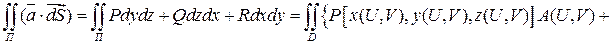

 (8)
(8)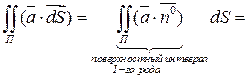 (по теореме о вычислении интеграла I-uj рода) =
(по теореме о вычислении интеграла I-uj рода) =  .
.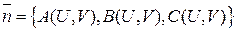 , приходим к скалярной записи формулы (8).
, приходим к скалярной записи формулы (8). и П задано вектором
и П задано вектором 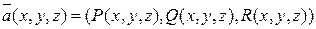 -непрерывное, то воспользовавшись тем, что:
-непрерывное, то воспользовавшись тем, что: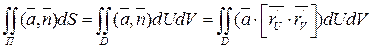 (*)
(*) запишем последнюю формулу (*) в координатной форме, т.е.:
запишем последнюю формулу (*) в координатной форме, т.е.: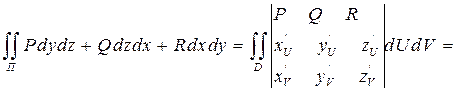 =
= 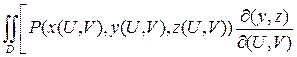 +
+ 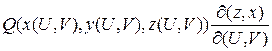 +
+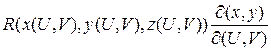
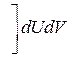 (8’)
(8’)
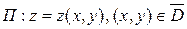 - гладкая ориентированная.
- гладкая ориентированная. 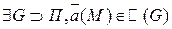 , тогда:
, тогда: (9)
(9) , где
, где  ,
, 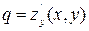 .
.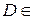 плоскости
плоскости  взаимнооднозначно. Иногда удобно применить второй способ вычисления поверхностных интегралов II-го рода – отдельно вычисляются составляющие интеграла.
взаимнооднозначно. Иногда удобно применить второй способ вычисления поверхностных интегралов II-го рода – отдельно вычисляются составляющие интеграла.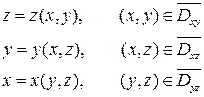
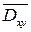 ,
,  ,
, 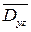 - взаимнооднозначные проекции П на координатные плоскости
- взаимнооднозначные проекции П на координатные плоскости  . Тогда:
. Тогда: (10)
(10) для этих случаев:
для этих случаев: Т.к.
Т.к. 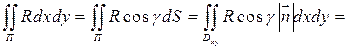
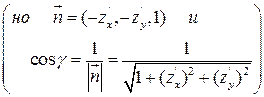 =
= - для внешней стороны.
- для внешней стороны.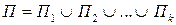 , так что условия теорем 4 и 5 выполняются.
, так что условия теорем 4 и 5 выполняются.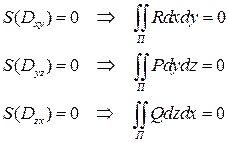
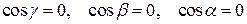 .
. 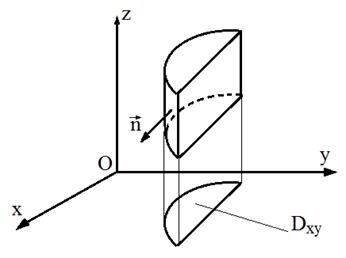
 .
. , учитывая
, учитывая 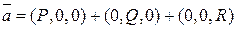 , тогда:
, тогда: 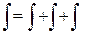 .
.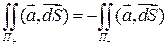 (11)
(11) - внутренняя сторона.
- внутренняя сторона.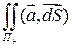 =
= 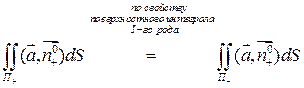 =
= 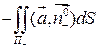 =
= 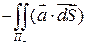 , т.к.
, т.к.  .
. - пунктирное разбиение П,
- пунктирное разбиение П, 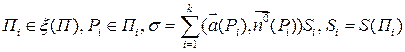 , тогда:
, тогда: (12)
(12) ,
,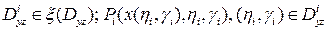 .
. ,
, .
. ,
,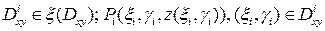 .
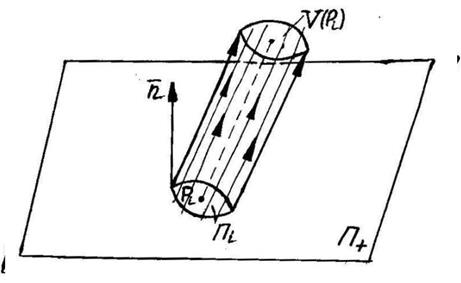
. .
.
 постоянная и
постоянная и 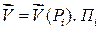 отождествляем с пластинкой с нормальным вектором
отождествляем с пластинкой с нормальным вектором 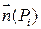 и площадкой
и площадкой 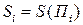 . Тогда естественно приближенно положить, что количество жидкости, вытекает через
. Тогда естественно приближенно положить, что количество жидкости, вытекает через 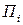 в единицу времени в направлении внешней стороны (
в единицу времени в направлении внешней стороны ( цилиндра) равно
цилиндра) равно 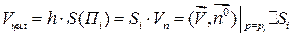 . Тогда положим, что через всю поверхность П вытекает за единицу времени:
. Тогда положим, что через всю поверхность П вытекает за единицу времени:
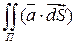 называется потоком вектора
называется потоком вектора 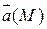 через ориентированную поверхность П называется интеграл по поверхности П от скалярного произведения
через ориентированную поверхность П называется интеграл по поверхности П от скалярного произведения 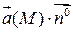 , где
, где 



