
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Физические приложения двойного интеграла.Содержание книги Поиск на нашем сайте
Пусть D – плоская пластина, лежащая в плоскости Оху с поверхностной плотностью ρ (х, у). Тогда: 1. массу m пластинки находят по формуле
2. статические моменты
3.кординаты центра тяжести
4. Моменты инерции
Для однородных пластинок поверхностная плотность Пример 1. Найти массу круглой пластины D Решение: Массу пластины вычисляем по формуле (10):
Поскольку пластина является круглой, вначале в двойном интеграле переходим к полярным координатам, а затем при вычислении внутреннего интеграла учитываем тот факт, что интеграл по периоду от тригонометрических функций равен нулю. Пример 2. Найти статический момент однородного прямоугольника со сторонами а и b относительно стороны а, считая, что прямоугольник лежит в плоскости Оху. Решение: Поместим начало координат в одну из вершин прямоугольника так, чтобы ось Ох совпадала со стороной а, а ось Оу – со стороной b. Статический момент прямоугольника относительно стороны а будет равен статическому моменту относительно оси Ох. По первой из формул (11) получаем:
Пример 3. Найти координаты центра тяжести однородной пластины плотности
Вычислим статические моменты пластины относительно координатных осей
Теперь вычисляем по формулам (12) координаты центра тяжести пластины:
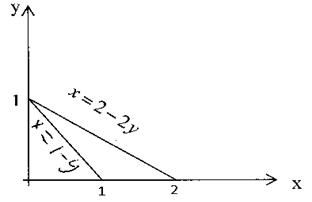
Пример 4. Вычислить моменты инерции однородного треугольника со сторонами х + у =1, х +2 у =2, у =0, относительно координатных осей.
Решение: Треугольник приведен на рис 28. Моменты инерции относительно осей вычисляем по формулам (13):
Рис.28
Пример 5. Найти момент инерции однородной области, ограниченной лемнискатой
Решение: Полярный момент инерции вычисляем по формуле (14), при этом в двойном интеграле перейдем к полярным координатам. В результате уравнение лемнискаты в полярных координатах принимает вид
Рис.29.
1.7. Задачи для самостоятельного решения:
Вычислить двойной интеграл:
1. 2. 3.
Двойной интеграл 4. D – треугольник с вершинами А (-1,-1), В (1,3), С (2,-4). 5. D – параллелограмм с вершинами А (-3,1), В (2,1), С (6,4), D (1,4). 6. D ограничена линиями 7. D ограничена линиями Изменить порядок интегрирования в повторном интеграле: 8. 10. 12. 14.
Выбирая подходящие замены переменных, вычислить двойные интегралы:
16. 17. 18.
В двойном интеграле
19. D – круг 20. D – область, ограниченная окружностями 21. D –область, ограниченная прямыми у = х, у =- х и у =1. 22. D – общая часть кругов Вычислить двойной интеграл, переходя к полярным координатам:
23. 24. 25. 26.
Вычислить площади фигур, ограниченных кривыми:
27. 29., ху =4, х + у -5=0. 30. 31. 33.
Вычислить объем тела, ограниченного поверхностями:
35. 37. 38. 39. Найти площадь части плоскости 40. Найти площадь части поверхности параболоида 41. Найти массу пластинки, ограниченной кривыми 42. Вычислить координаты центра тяжести фигуры, ограниченной кардиоидой 43. Найти координаты центра тяжести однородной пластики, ограниченной параболой 44. Найти координаты центра тяжести однородной пластинки, ограниченной окружностью 45. Найти статический момент однородного полукруга радиуса R, лежащего в плоскости Оху, относительно диаметра.
46. Найти статические моменты относительно осей Ох и Оу однородной пластины, ограниченной кардиоидой 47. Найти статические моменты однородной пластины, ограниченной кривой y =sin x и прямой ОА, проходящей через начало координат и точку 48. Найти моменты инерции прямоугольника ОАСВ со сторонами ОА = а и ОВ = b относительно вершины О и сторон ОА и ОВ, если его плотность равна расстоянию до стороны ОВ, считая, что прямоугольник лежит в плоскости Оуz. 49. Найти моменты инерции однородной пластины, ограниченной эллипсом 50. Найти полярный момент инерции однородной фигуры, ограниченной кардиоидой Глава 2. ТРОЙНЫЕ ИНТЕГРАЛЫ.
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 6576; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.187.31 (0.007 с.) |

 (10)
(10) и
и  пластинки относительно координатных осей находят по формулам
пластинки относительно координатных осей находят по формулам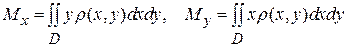 (11)
(11)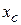 и
и 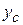 пластинки – по формулам
пластинки – по формулам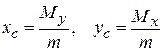 (12)
(12) ,
,  и
и 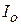 пластинки соответственно относительно координатных осей Ох и Оу и начала координат находят по формулам
пластинки соответственно относительно координатных осей Ох и Оу и начала координат находят по формулам (13)
(13)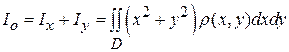 (14)
(14)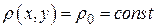 . В некоторых задачах для простоты полагают
. В некоторых задачах для простоты полагают  .
.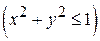 с поверхностной плотностью ρ (х, у)=3- х - у.
с поверхностной плотностью ρ (х, у)=3- х - у.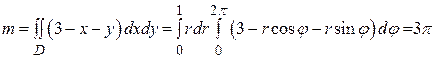
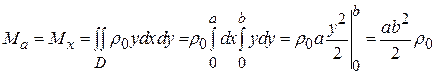
 , ограниченной параболой
, ограниченной параболой  и прямой х + у =2.
и прямой х + у =2.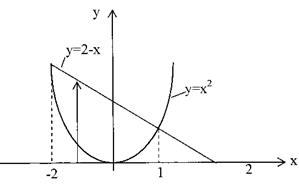 Решение: Чертеж области приведен на рис.27. Найдем абсциссы точек пересечения графиков. Из системы
Решение: Чертеж области приведен на рис.27. Найдем абсциссы точек пересечения графиков. Из системы  получаем
получаем  и
и  . Тогда масса пластины вычисляется по формуле:
. Тогда масса пластины вычисляется по формуле: Рис.27.
Рис.27.

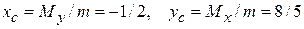


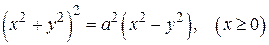 относительно начала координат.
относительно начала координат.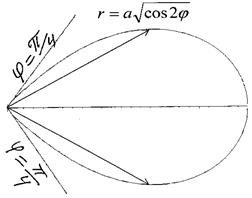
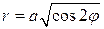 , а координата
, а координата  (рис. 29). Тогда получаем:
(рис. 29). Тогда получаем: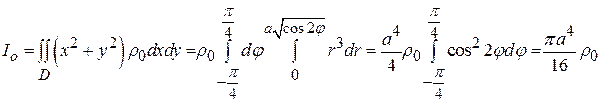
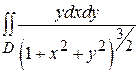 , где D – прямоугольник
, где D – прямоугольник 
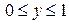 .
.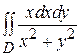 , где D - ограниченна параболой
, где D - ограниченна параболой  и прямой у = х.
и прямой у = х.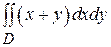 , D ограничена линиями
, D ограничена линиями  , х =0, 2 у =3 х.
, х =0, 2 у =3 х. представить в виде повторного двумя способами:
представить в виде повторного двумя способами: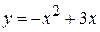 ,
, 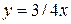 .
. .
.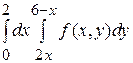 9.
9. 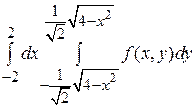
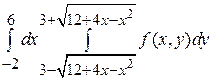 11.
11. 
 13.
13. 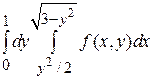
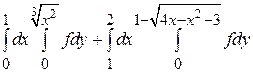 15.
15. 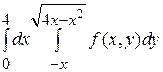
 , где D ограничена линиями
, где D ограничена линиями 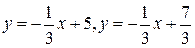 , у = х +1, у = х -3.
, у = х +1, у = х -3. , где D – параллелограмм со сторонами у = х, у = х +3, у =-2 х +1, у =-2 х+5.
, где D – параллелограмм со сторонами у = х, у = х +3, у =-2 х +1, у =-2 х+5. , D ограничена кривыми
, D ограничена кривыми  , ху = p, ху = q (0< a < b, 0< p < q).
, ху = p, ху = q (0< a < b, 0< p < q).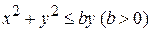 .
.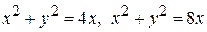 и прямыми у = х и у =2 х.
и прямыми у = х и у =2 х.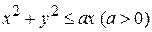 и
и  .
. , D ограничена лемнискатой
, D ограничена лемнискатой 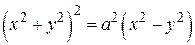 .
. , где D – круг
, где D – круг  .
. , где D – четверть круга
, где D – четверть круга  .
. , у = х. 28.
, у = х. 28.  ,
,  .
. , х + у = а
, х + у = а , у = х, у =0. 32.
, у = х, у =0. 32.  , у =-1, у =- х.
, у =-1, у =- х. . 34.
. 34.  .
.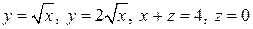 . 36.
. 36. 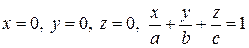 .
.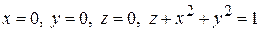 .
.
 , лежащей в первом октанте.
, лежащей в первом октанте. , отсекаемой цилиндром
, отсекаемой цилиндром 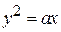 и плоскостью х =3 а.
и плоскостью х =3 а.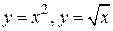 , если ее плотность равна ρ (х, у)= х +2 у.
, если ее плотность равна ρ (х, у)= х +2 у.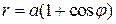 .
.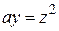 и прямой у =2 (а >0).
и прямой у =2 (а >0). и двумя радиусами у =0 и у = х tg α.
и двумя радиусами у =0 и у = х tg α.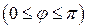 и полярной осью.
и полярной осью. (
(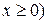 ,относительно осей Ох и Оу.
,относительно осей Ох и Оу. , относительно осей Ох, Оу и относительно начала координат.
, относительно осей Ох, Оу и относительно начала координат.


