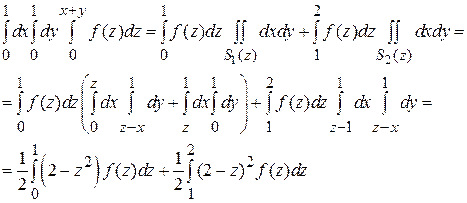Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тройной интеграл в декартовых координатах.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Тройной интеграл является обобщением интеграла Римана на случай функции трех переменных. Определение тройного интеграла, а также его свойства аналогичны определению и свойствам двойного интеграла. Определение: Тройным интегралом от непрерывной функции u = f(x, y, z) по ограниченной кубируемой (измеримой по Жордану) области G называется
Вычисляют тройной интеграл также как и двойной, сведением к повторным интегралам, при этом порядок следования переменных выбирается так, чтобы упростить проводимые вычисления. Пусть область G из пространства Охуz проектируется в область D плоскости Оху так, что всякая прямая, параллельная оси Оz и проходящая внутри области D, пересекает границу тела только в двух точках. В общем случае такая область ограничена снизу поверхностью
Рис.30 Рис.31
Тройной интеграл по такой области вычисляется по формуле:
Здесь внутренний интеграл Наиболее простой вид формула (15) принимает в случае, когда областью интегрирования является прямоугольный параллелепипед, ограниченный плоскостями x = a, x = b, y = c, y = d, z = p, z = q (a < b, c < d, p < q) и пределы интегрирования по всем трем переменным являются константами
Если область G имеет более сложную форму, то ее разбивают на конечное число областей, удовлетворяющих приведенным выше условиям. Замечание: Аналогичные определения и формулы могут получены и тогда, когда область G проектируется в область D, лежащую в плоскости Охz или Оуz.
Пример 1: Вычислить интеграл Решение: Для правильной расстановки пределов интегрирования построим область G (рис.32). Область интегрирования G представляет фигуру, проекция которой на плоскость Oху есть треугольник с координатами вершин (0,0,0), (1,0,0), (0,1,0).
Рис.33 Очевидно, что нижняя граница области G – плоскость z =0, а верхняя – плоскость z =1- х - у, это и будут пределы интегрирования по z. Для расстановки пределов по x и y в области D воспользуемся опытом вычисления двойных интегралов. Область D приведена на рис.33. Из рисунка видно, что x меняется в пределах от 0 до 1, а у от 0 до значения на прямой y =1- x:
Решение: Область G ограничена снизу плоскостью z =0, а сверху- поверхностью гиперболического параболоида (рис.34). Проекцией данной области на плоскость Оху является треугольник, образованный осями координат х =0, у =0 и прямой х + у =1 (рис.33). Поэтому тройной интеграл сводится к повторным следующим образом:
Рис.34
Возможен и другой подход к вычислению интеграла, когда в качестве внешнего интеграла удобно выбрать интеграл по z и расставлять пределы внутренних интегралов, используя сечение фигуры плоскостью z =const. В этом случае применяют формулу:
где S (z) –сечение объема плоскостью z =const.
Пример 3: Вычислить интеграл
Рис.35а Рис.35б
уравнения границ находим значения для переменных x и y. Подставим пределы в интеграл
Пример 4: Заменить тройной интеграл Решение: Построим область G, ограниченную плоскостями х =0, х =1, у =0, у =1, z =0, z = х + у (рис.36а). Чтобы свести тройной интеграл к однократному, внешний интеграл нужно взять по переменной z, т.к. подынтегральная функция является функцией z. Проведем сечение объема плоскостью z =const, причем при 0< z <1 сечение приведено на рис.36б, а при 1< z <2 – на рис.36в.
Рис.36а
Рис.36б Рис.36в
Тогда интеграл можно переписать в виде
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1594; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.77.29 (0.011 с.) |

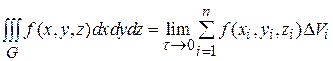 , где
, где 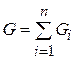 - разбиение области G на кубируемые части Gi,
- разбиение области G на кубируемые части Gi, 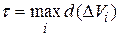 - максимальный диаметр объема разбиения Δ Vi.
- максимальный диаметр объема разбиения Δ Vi.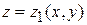 , сверху – поверхностью
, сверху – поверхностью 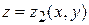 , а с боков – цилиндрической поверхностью с образующими, параллельными оси Оz (рис.30). В частных случая боковая поверхность цилиндра может превратиться в линию (рис.31).
, а с боков – цилиндрической поверхностью с образующими, параллельными оси Оz (рис.30). В частных случая боковая поверхность цилиндра может превратиться в линию (рис.31).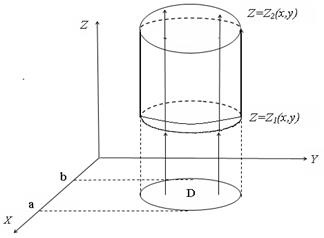

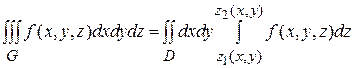 (15)
(15)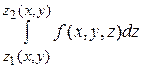 берется по z от нижней границы области G до ее верхней границы при фиксированных, но произвольных в области D значениях х и у. В результате получается некоторая функция от х и у, которая затем интегрируется в области D.
берется по z от нижней границы области G до ее верхней границы при фиксированных, но произвольных в области D значениях х и у. В результате получается некоторая функция от х и у, которая затем интегрируется в области D.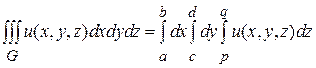 (16)
(16)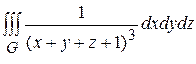 , где G – область, ограниченная плоскостями x =0, y =0, z =0, x + y + z =1.
, где G – область, ограниченная плоскостями x =0, y =0, z =0, x + y + z =1.

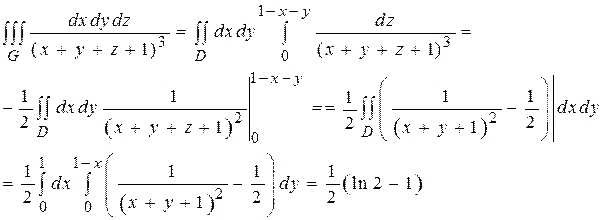
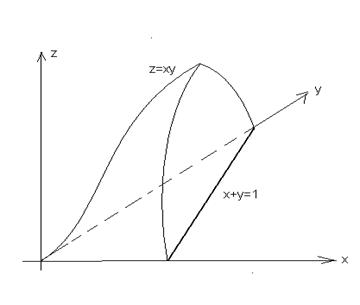 Пример 2: Вычислить интеграл
Пример 2: Вычислить интеграл 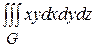 , если область G ограничена гиперболическим параболоидом z = xу и плоскостями x + y =1 и z =0 (z >0).
, если область G ограничена гиперболическим параболоидом z = xу и плоскостями x + y =1 и z =0 (z >0).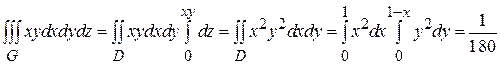
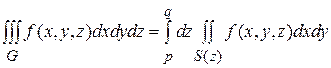 , (17)
, (17)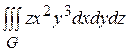 , где G - объем, ограниченный плоскостями у =0, y = x, z =1, z = x.
, где G - объем, ограниченный плоскостями у =0, y = x, z =1, z = x.
 Решение: Построим область интегрирования (рис.35а). Выберем z в качестве внешней переменной интегрирования. Из уравнения границ видно, что z меняется от 0 до 1. Построим сечение фигуры плоскостью z =const (рис 35б) и из
Решение: Построим область интегрирования (рис.35а). Выберем z в качестве внешней переменной интегрирования. Из уравнения границ видно, что z меняется от 0 до 1. Построим сечение фигуры плоскостью z =const (рис 35б) и из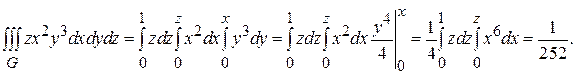
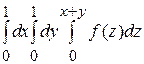 однократным.
однократным.