
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Переход к полярным координатам в двойном интеграле.Содержание книги Поиск на нашем сайте
Важнейшимчастным случаем криволинейных координат являются полярные координаты (r, φ). Они связаны с прямоугольными координатами формулами:
Переходить к полярным координатам удобно в тех случаях, когда область интегрирования есть круг, кольцо или их часть, а так же в случае, когда подынтегральная функция имеет вид Интегрирование в полярных координатах проводится по координатным линиям r =const и φ =const. Линии r =const представляют из себя окружности с центром в начале координат. По окружностям происходит изменение координаты φ. Линии φ =const – это семейства лучей, выходящих из начала координат, по которым происходит изменение координаты r. Координатная сетка в полярных координатах изображена на рис.18.
Рис.17а Рис.17б Рис.18
Пусть область D расположена между лучами φ = α и φ = β, где α< β, и ограничена линиями двух точках (простая область относительно r) (рис.19).Тогда двойной интеграл сводится к повторному по формуле:
Рис.19 Рис.20
Пусть область D расположена между окружностями r = а и r = b, где а< b и ограничена линиями
Пример 1. Вычислить двойной интеграл Решение: Как уже говорилось выше, если интегрирование ведется по кругу, то уравнение его границы в полярных координатах имеет вид r =1, а на плоскости Оrφ область Ω является прямоугольником
Решение: Область D изображена на рис.21. Переведем ее границы в полярные координаты: уравнение окружности имеет вид r = a, а отрезки прямых y = x Рис.21
Пример 3. В двойном интеграле Решение: Чтобы построить область D, приведем уравнение кривой к каноническому виду, для чего выделяем полный квадрат по переменной х:
Рис.22а Рис.22б
Переведем границу области D в полярные координаты, для этого удобнее воспользоваться уравнением окружности в виде лучи при
Чтобы расставить пределы интегрирования в другом порядке, определим границы изменения координаты r. Для этого проведем координатные линии r =const, пересекающие область D, и определим окружности, которые касаются нашей области. Очевидно, что это будут линии r =0 и r =2 а, так что r изменяется в пределах от 0 до а (рис.22б). Для нахождения границ изменения переменной φ уравнение окружности
Пример 4. В двойном интеграле Решение: Кривая
Рис.23а Рис.23б
Проведем линии r =const и определяем, что область заключена между координатными линиями r =1 и r =2, а координатная линия
Замечание: В некоторых случаях, если область интегрирования в двойном интеграле ограничена окружностью Пример 5. Вычислить интеграл Замечание: В случае, когда область интегрирования в двойном интеграле является эллипс или его часть, то вводят обобщенные полярные или эллиптические координаты Решение: Перейдем к эллиптическим координатам, при этом границы эллиптического кольца принимают вид r =1 и r =2, а вся область расположена между лучами φ =0 и
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 14491; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.214.16 (0.006 с.) |

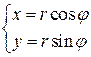 ,
,  . Якобиан преобразования в этом случае
. Якобиан преобразования в этом случае 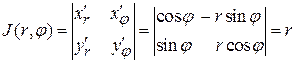 , а формула перехода к полярным координатам в двойном интеграле имеет вид:
, а формула перехода к полярным координатам в двойном интеграле имеет вид: (4)
(4) . В полярных координатах выражение
. В полярных координатах выражение  . Границей круга является окружность
. Границей круга является окружность  и ее уравнение в полярных координатах принимает вид: r = R. Тогда область D - круг
и ее уравнение в полярных координатах принимает вид: r = R. Тогда область D - круг  в полярной системе координат на плоскости Оrφ переходит в прямоугольную область Ω, которая задается неравенствами:
в полярной системе координат на плоскости Оrφ переходит в прямоугольную область Ω, которая задается неравенствами: 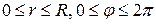 (рис.17а,б).
(рис.17а,б).

 и
и  , где
, где 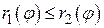 и любой луч, выходящий из полюса φ =const (
и любой луч, выходящий из полюса φ =const ( ) пересекает ее границу не более чем в
) пересекает ее границу не более чем в

 (5)
(5) и
и  , где
, где  и любая окружность радиуса r =const (
и любая окружность радиуса r =const (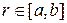 ) пересекает границу области не более чем в двух точках (правильная относительно φ) (рис.20). В этом случае двойной интеграл сводится к повторному по формуле:
) пересекает границу области не более чем в двух точках (правильная относительно φ) (рис.20). В этом случае двойной интеграл сводится к повторному по формуле: 6)
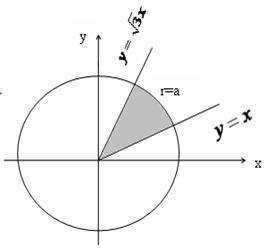
6) , где область D ограничена окружностью
, где область D ограничена окружностью  .
. . Осталось записать в полярных координатах подынтегральную функцию:
. Осталось записать в полярных координатах подынтегральную функцию:  . Вычисляем интеграл
. Вычисляем интеграл
 Пример 2. Вычислить
Пример 2. Вычислить  , если область D ограничена окружностью
, если область D ограничена окружностью  , лежащей в первой четверти, и прямыми y = x и
, лежащей в первой четверти, и прямыми y = x и  .
. и
и  . Проводя лучи φ =const
. Проводя лучи φ =const  , определяем, что координата r изменяется от 0 до а. Тогда по формуле (5) получаем:
, определяем, что координата r изменяется от 0 до а. Тогда по формуле (5) получаем:
 перейти к полярным координатам и расставить пределы интеграции в том и другом порядке, если область D ограничена кривой
перейти к полярным координатам и расставить пределы интеграции в том и другом порядке, если область D ограничена кривой  .
.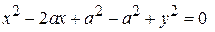 ,
,  . Получаем уравнение окружности с центром на оси Ох в точке х = а, у =0, радиуса а, при этом окружность касается оси Оу (рис.22а,б).
. Получаем уравнение окружности с центром на оси Ох в точке х = а, у =0, радиуса а, при этом окружность касается оси Оу (рис.22а,б).

 :
: 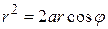 или
или  . Область D находится между лучами
. Область D находится между лучами  и
и  и проводя
и проводя , определяем, что координата r изменяется от 0 в начале координат до значения радиуса на окружности, т.е. до значения
, определяем, что координата r изменяется от 0 в начале координат до значения радиуса на окружности, т.е. до значения 
 или
или  . Для нижней ветви окружности берется знак «-», а для верхней ветви – знак «+». Теперь по координатным линиям r =const, которые пересекают область D, определяем границы изменения φ: от значения на нижней ветви окружности до значения на верхней ветви окружности. В результате по формуле (6) получаем:
. Для нижней ветви окружности берется знак «-», а для верхней ветви – знак «+». Теперь по координатным линиям r =const, которые пересекают область D, определяем границы изменения φ: от значения на нижней ветви окружности до значения на верхней ветви окружности. В результате по формуле (6) получаем:
 перейти к полярным координатам и расставить пределы интеграции в том и другом порядке, если область D ограничена линиями
перейти к полярным координатам и расставить пределы интеграции в том и другом порядке, если область D ограничена линиями 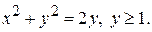
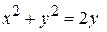 является уравнением окружности с центром в точке (0,1):
является уравнением окружности с центром в точке (0,1):  . При
. При  выбирается верхняя половина круга – это и будет область D. Переведем границы области в полярные координаты, при этом уравнение окружности имеет вид
выбирается верхняя половина круга – это и будет область D. Переведем границы области в полярные координаты, при этом уравнение окружности имеет вид 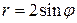 . Если из него выразить φ, получаем
. Если из него выразить φ, получаем  для правой ветки окружности и
для правой ветки окружности и  - для левой. Прямая y=1 в полярных координатах имеет уравнение
- для левой. Прямая y=1 в полярных координатах имеет уравнение  или
или  и
и  для отрезков прямых, лежащих в первой и во второй четверти соответственно. Нанесем координатные линии φ =const, откуда определяем, что область D расположена между лучами
для отрезков прямых, лежащих в первой и во второй четверти соответственно. Нанесем координатные линии φ =const, откуда определяем, что область D расположена между лучами 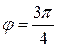 , а радиус изменяется от значения на отрезке прямой y=1 до значения на дуге окружности (рис.23а). Тогда получаем:
, а радиус изменяется от значения на отрезке прямой y=1 до значения на дуге окружности (рис.23а). Тогда получаем: .
.

 проходит через точки (±1,1), в которых пересекаются границы области - окружность и прямая (рис.23б). Поэтому D необходимо разбить на две простые области относительно φ:
проходит через точки (±1,1), в которых пересекаются границы области - окружность и прямая (рис.23б). Поэтому D необходимо разбить на две простые области относительно φ: 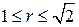 и
и 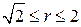 и пределы интегрирования в двойном интеграле расставляются так:
и пределы интегрирования в двойном интеграле расставляются так:
 , удобнее делать замену
, удобнее делать замену  . При такой замене осуществляется параллельный перенос системы координат в центр окружности, а якобиан преобразования при этом не изменяется, т.е. J = r (предлагается убедиться в этом самостоятельно). В частности, если в примере 4 ввести замену
. При такой замене осуществляется параллельный перенос системы координат в центр окружности, а якобиан преобразования при этом не изменяется, т.е. J = r (предлагается убедиться в этом самостоятельно). В частности, если в примере 4 ввести замену  , то уравнение окружности
, то уравнение окружности  преобразуется к виду r =1, а область интегрирования Ω в координатах Оrφ становится прямоугольной:
преобразуется к виду r =1, а область интегрирования Ω в координатах Оrφ становится прямоугольной:  .
. , где область D – лежащая в первой четверти часть эллиптического кольца
, где область D – лежащая в первой четверти часть эллиптического кольца  .
. . При этом J = abr (проверить самостоятельно), а выражение
. При этом J = abr (проверить самостоятельно), а выражение  преобразуется в выражение
преобразуется в выражение 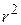 .
.



