
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Семерикова Н.П., Лапинова С.А.,
КРАТНЫЕ ИНТЕГРАЛЫ
Электронное учебно-методическое пособие
Мероприятие 1.2. Совершенствование образовательных технологий, укрепление материально-технической базы учебного процесса
Нижний Новгород
КРАТНЫЕ ИНТЕГРАЛЫ. Семерикова Н.П., Лапинова С.А. Электронное учебно-методическое пособие. – Нижний Новгород: Нижегородский госуниверситет, 2012. – 57 с.
В учебно-методическом пособии рассматриваются задачи по одной из важнейших тем математического анализа – двойным и тройным интегралам. В пособии разбираются такие темы, как расстановка пределов интеграции в двойных интегралах, переход в двойном интеграле к полярным и произвольным криволинейным координатам. Рассмотрены задачи, связанные с вычислением тройных интегралов в декартовых, цилиндрических и сферических координатах. Разобраны задачи на геометрические и механические приложения кратных интегралов – вычисления площадей и объемов тел, вычисление массы, координат центра тяжести, статических моментов и моментов инерции тел. По каждой из тем пособие содержит задачи для самостоятельного решения Электронное учебно-методическое пособие предназначено для студентов ННГУ, обучающихся по направлению подготовки 011800.62 «Радиофизика», изучающих курс «Кратные интегралы и ряды», по направлению 010300.62 «Фундаментальная информтика и информационные технологии», изучающих курс «Кратные интегралы и ряды» и по направлению 090302.65 «Информационная безопасность телекоммуникационных систем», изучающих курс «Математический анализ».
ОГЛАВЛЕНИЕ
ГЛАВА 1. Двойные интегралы. ………….…………….………….…………….4 1.1. Двойной интеграл – основные понятия и определения………….……………..………….…………….……………..4 1.2. Вычисление двойного интеграла в декартовых координатах…………………….…………….………….…………………6 1.3. Замена переменных в двойном интеграле (общий случай)…………… ………….………………….………….……………..15 1.4. Переход к полярным координатам в двойном интеграле……………………….……….………….…………….………..19 1.5. Геометрические приложения двойного интеграла…………………….……….…………….…………….……......24 1.6. Физические приложения двойного интеграла……….……………..27
1.7. Задачи для самостоятельного решения……………………………..29
ГЛАВА 2. Тройные интегралы………………………………………………….33 2.1. Тройной интеграл в декартовых координатах……………………...33 2.2. Замена переменных в тройном интеграле…………………………..37 2.3. Вычисление тройного интеграла в цилиндрических координатах.39 2.4. Вычисление тройного интеграла в сферических координатах……42 2.5. Приложения тройного интеграла……………………………………47 2.6. Задачи для самостоятельного решения……………………………..49 Ответы……………………………………………………………………………52 Список литературы………………………………………………………………54 Глава 1. ДВОЙНЫЕ ИНТЕГРАЛЫ
1.1. Двойной интеграл – основные понятия и определения. Двойной интеграл является обобщением определенного интеграла на случай функции двух переменных.
Определение двойного интеграла: Предел при Таким образом, двойной интеграл определяется равенством В этом случае функция Геометрический смысл двойного интеграла:
Рассмотрим тело, ограниченное сверху поверхностью z=f (x,y)>0, снизу –замкнутой областью D плоскости Oxy, с боков – цилиндрической поверхностью с образующей - параллельной оси Oz, а направляющей служит граница области D (рис. 2). Такое тело называется цилиндрическим. Составим для функции
Итак, геометрический смысл двойного интеграла от неотрицательной функции – объем цилиндрического тела. В частности, если считать
Физический смысл двойного интеграла: Требуется найти массу плоской пластины, если известна ее поверхностная плотность ρ (x, y). Разобьем область D на n «элементарных областей» отличается от значений
Простейшие свойства двойного интеграла. Эти свойства используются для вычисления двойного интеграла и аналогичны свойствам определенного интеграла. Пусть
1. 2. 3. Если область D разбить линией на две области
1.2. Вычисление двойного интеграла в декартовых координатах.
Всякая прямая, параллельная оси Oy и проходящая внутри отрезка [ a, b ] пересекает границу простой области (I) в двух точках (см. рис.3, 4). В случае простой области (I) (
Таким образом, вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов, которые называются повторными. Для применения формулы (1) область D необходимо спроектировать на ось Ох и получить отрезок [ a, b ] (рис.3,4), границы x = a и x = b которого являются пределами интегрирования во внешнем интеграле. Затем проводим координатные линии x = const, пересекающие область D и определяем нижнюю и верхнюю границы области. Интегрирование по координатной линии x = const всегда ведется в направлении оси Оу.
Определение 2: Область D на плоскости Oxy назовем простой областью вида (II) (относительно оси Oy), если она ограничена слева линией
Всякая прямая, параллельная оси Ox и проходящая внутри отрезка[ c,d ], пересекает границу простой области (II) в двух точках (см. рис.5,6). В случае простой области (II) (
Здесь интегрирование во внутреннем интеграле ведется по х при фиксированном значении Для применения формулы (2) область D проектируем на ось Оy и получаем отрезок [ c, d ] (рис.5,6), границы которого y = c и y = d являются пределами интегрирования во внешнем интеграле. Затем проводим координатные линии y = const, пересекающие область D и определяем левую и правую границы области. Интегрирование по координатной линии y = const всегда ведется в направлении оси Ох.
Важно помнить, что во внешнем интеграле в формулах (1) и (2) пределами интегрирования всегда являются числа.
Наиболее простой вид формулы (1) и (2) принимают в случае прямоугольной области D, ограниченной прямыми x = a, x = b, y = c, y = d. Прямоугольник
Замечания: 1. Если область D является простой областью вида (I) и (II), то для вычисления двойного интеграла можно применять и формулу (1), и формулу (2):
2. Если область D не является простой областью вида (I) или (II), то при помощи прямых, параллельных координатным осям ее разбивают на конечное число простых областей и для вычисления двойного интеграла используется третье свойство двойного интеграла. 3. Аналогичные определения и формулы справедливы и тогда, когда замкнутая область D лежит либо в плоскости xOz, либо в плоскости yOz. Например, если ограниченная замкнутая область D лежит в плоскости xOz и является простой относительно оси Oz, а в ней задана непрерывная функция y = f (x, z), то
Пример 1. Вычислить интеграл Решение: Для прямоугольной области применяем формулу (3):
Сначала вычисляем внутренний интеграл, считая переменную x константой:
После подстановки пределов интегрирования по y, получаем функцию от х I (x)=2 x +4, которую интегрируем по отрезку [1,2]:
Пример 2. Вычислить интеграл
Решение: Как и в примере 1, двойной интеграл сводится к повторному по формуле (3): При вычислении внутреннего интеграла по у, считаем х константой, которую по первому свойству двойного интеграла (см. п.1.1), выносим за знак интеграла:
В данном примере удобнее воспользоваться еще одним свойством двойного интеграла. Если подынтегральная функция f (x, y)= X (x) Y (y) является произведением двух функций, одна из которых зависит только от x, а вторая - от y, и область интегрирования является прямоугольной
Решение: Область D является простой областью типа (I), так как любая прямая, параллельная оси Оу, пересекает границу области только в двух точках (рис.7). При любом фиксированном значении х из отрезка [0,π] координата y меняется от y =0 до y =1+cos x. Поэтому для вычисления интеграла воспользуемся формулой (1):
Отметим, что для вычисления данного интеграла можно было воспользоваться и формулой (2), т.к. область D также является простой областью вида (II). Но в этом случае границы области нужно задавать в виде х = х (у), что приводит к более громоздким вычислениям.
Решение: Область D является простой областью относительно оси Оу, т.е. областью вида (II). Левая ее граница x =0, а правая - x =2+sin y (рис.8). При любом фиксированном значении у из отрезка [0,2π] определяем, что координата х изменяется от x =0 до x =2+sin y. Поэтому по формуле (2) имеем:
Пример 5. В двойном интеграле Решение: Область D изображена на рис.9. Она является простой областью вида (I) и (II), поэтому для расстановки пределов интегрирования в двойном интеграле воспользуемся формулами (1) и (2).
Для применения формулы (2) область интегрирования D проектируем на ось y и получаем отрезок [0,1],а затем проводим координатные линии x = cоnst и определяем, что левая граница x =0, а правая граница - прямая x = y. Тогда двойной интеграл преобразуется к виду:
Пример 6. В двойном интеграле
Область D является простой областью относительно оси Oх, она находится в полосе между прямыми x =0 и x =1. Ее нижней границей является дуга окружности Для расстановки пределов интегрирования в другом порядке проектируем область D на ось Oу и получаем отрезок [-1,1]. Из рис.10 видно, что область D ограничена слева дугой окружности
Пример 7. В двойном интеграле
Проектируем D на ось Oх и получаем отрезок [0,7]. При этом нижней границей области D являются прямые y =0 при
Для второго способа расстановки пределов интегрирования проектируем область D на ось Oу и разбиваем ее на две области. В первой области при
Пример 8. Изменить порядок интегрирования в интеграле Решение: Область D расположена между прямыми x =0 и x =1. Ее нижняя граница - прямая у = х, а верхняя
Пример 9. Изменить порядок интегрирования в повторном интеграле
Рис. 13
Повторный интеграл принимает вид:
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 500; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.172.115 (0.074 с.) |
 Пусть в замкнутой области D на плоскости Oxy задана непрерывная функция z=f (x,y). Разобьем область D на n «элементарных областей»
Пусть в замкнутой области D на плоскости Oxy задана непрерывная функция z=f (x,y). Разобьем область D на n «элементарных областей»  (i= 1 ,n), площади которых обозначим через
(i= 1 ,n), площади которых обозначим через  (рис.1). В каждой области
(рис.1). В каждой области  , умножим значение функции
, умножим значение функции  в этой точке на
в этой точке на  и составим интегральную сумму:
и составим интегральную сумму: .
. интегральных сумм
интегральных сумм  , не зависящий от способа разбиения области D на части
, не зависящий от способа разбиения области D на части  , называется двойным интегралом от функции
, называется двойным интегралом от функции  по области D. и обозначается
по области D. и обозначается  .
. . Если разбиение области D проводить прямыми параллельными координатным осям, то элемент площади ds = dxdy и двойной интеграл в декартовых координатах записывается в виде
. Если разбиение области D проводить прямыми параллельными координатным осям, то элемент площади ds = dxdy и двойной интеграл в декартовых координатах записывается в виде  .
.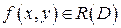 , а область D называется областью интегрирования. Всякая непрерывная в ограниченной замкнутой области D функция
, а область D называется областью интегрирования. Всякая непрерывная в ограниченной замкнутой области D функция 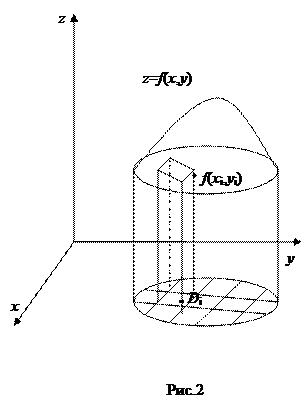
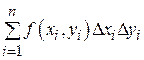 , при этом каждое слагаемое в интегральной сумме определяет объем элементарного параллелепипеда с основанием
, при этом каждое слагаемое в интегральной сумме определяет объем элементарного параллелепипеда с основанием  . Тогда объем цилиндрического тела
. Тогда объем цилиндрического тела  . Это равенство тем точнее, чем больше число n и чем меньше размеры элементарных областей
. Это равенство тем точнее, чем больше число n и чем меньше размеры элементарных областей 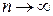 ), а каждая площадка
), а каждая площадка  .
.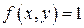 , то численно значение двойного интеграла будет равно площади области D
, то численно значение двойного интеграла будет равно площади области D .
. . Если области
. Если области  мало
мало . Тогда масса всей пластины задается приближенным равенством
. Тогда масса всей пластины задается приближенным равенством  . Точное значение массы получим при условии
. Точное значение массы получим при условии  .
. и с – const. Тогда:
и с – const. Тогда: .
.
 и
и  , такие, что
, такие, что  ,а пересечение
,а пересечение  .
.
 Определение 1: Область D на плоскости Oxy назовем простой областью вида (I) (простой относительно оси Ox), если она ограничена снизу линией
Определение 1: Область D на плоскости Oxy назовем простой областью вида (I) (простой относительно оси Ox), если она ограничена снизу линией  , сверху -
, сверху -  (где
(где 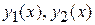 непрерывные функции) и с боков – отрезками прямых x = a, x = b (рис.3). В частных случаях один из этих отрезков (или оба вместе) могут превратиться в точку (рис.4). Область вида (I) задается неравенствами
непрерывные функции) и с боков – отрезками прямых x = a, x = b (рис.3). В частных случаях один из этих отрезков (или оба вместе) могут превратиться в точку (рис.4). Область вида (I) задается неравенствами  .
. (1) Здесь сначала вычисляется внутренний интеграл по y. Он берется при каждом фиксированном значении
(1) Здесь сначала вычисляется внутренний интеграл по y. Он берется при каждом фиксированном значении  от нижней границы области D
от нижней границы области D  , которая затем интегрируется по отрезку [ a, b ], т.е.
, которая затем интегрируется по отрезку [ a, b ], т.е.  .
. , справа -
, справа -  (где
(где  непрерывные функции), а сверху и снизу – отрезками прямых y = c, y = d (рис.5). В частных случаях один из этих отрезков (или оба вместе) могут превратиться в точку (рис.6). Область вида (II) задается неравенствами
непрерывные функции), а сверху и снизу – отрезками прямых y = c, y = d (рис.5). В частных случаях один из этих отрезков (или оба вместе) могут превратиться в точку (рис.6). Область вида (II) задается неравенствами  .
.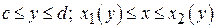 , где
, где 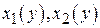 -
-
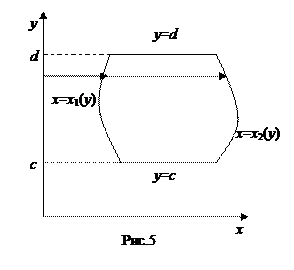
 непрерывные функции на [ c, d ]), двойной интеграл вычисляется по формуле:
непрерывные функции на [ c, d ]), двойной интеграл вычисляется по формуле: (2)
(2) от левой границы области
от левой границы области  является одновременно простой областью вида (I) и (II) и для вычисления двойного интеграла можно применять любую из формул (1) и (2):
является одновременно простой областью вида (I) и (II) и для вычисления двойного интеграла можно применять любую из формул (1) и (2):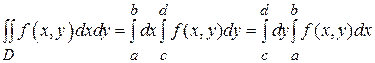 (3)
(3)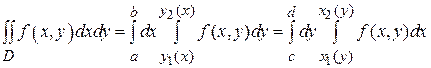

 , где
, где  .
.
 .
.
 , где
, где 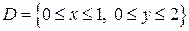 .
.
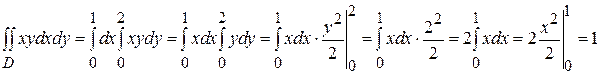
 . В этом случае результат вычисления внутреннего интеграла есть число. Поэтому решение задачи 2 кратко можно записать так:
. В этом случае результат вычисления внутреннего интеграла есть число. Поэтому решение задачи 2 кратко можно записать так:
 Пример 3. Вычислить интеграл
Пример 3. Вычислить интеграл  , где область D ограничена линиями x =0, y =0, x = π, y =1+cos x.
, где область D ограничена линиями x =0, y =0, x = π, y =1+cos x.
 Пример 4. Вычислить интеграл
Пример 4. Вычислить интеграл  , если область D ограничена кривой x =2+sin y и прямыми x =0, y =0, у=2π.
, если область D ограничена кривой x =2+sin y и прямыми x =0, y =0, у=2π.
 расставить пределы интеграции в том и другом порядке, если область D – треугольник с вершинами в точках O (0,0), A (1,0), B (1,1).
расставить пределы интеграции в том и другом порядке, если область D – треугольник с вершинами в точках O (0,0), A (1,0), B (1,1). Для применения формулы (1) область D проектируем на ось Oх и получим отрезок [0,1] – это пределы интегрирования во внешнем интеграле. Далее для расстановки пределов интегрирования во внутреннем интеграле при любом фиксированном
Для применения формулы (1) область D проектируем на ось Oх и получим отрезок [0,1] – это пределы интегрирования во внешнем интеграле. Далее для расстановки пределов интегрирования во внутреннем интеграле при любом фиксированном  проводим координатные линии y = cоns t и по ним определяем, что нижняя граница области D y =0, а верхняя граница – прямая y = x. Таким образом получим:
проводим координатные линии y = cоns t и по ним определяем, что нижняя граница области D y =0, а верхняя граница – прямая y = x. Таким образом получим: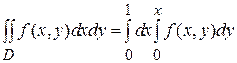 .
. .
.
 Решение: Построим область D, но вначале нужно понять, как нарисовать кривую
Решение: Построим область D, но вначале нужно понять, как нарисовать кривую  и
и  , т.е.
, т.е.  . Получаем:
. Получаем:  . Теперь все слагаемые перенесем в левую часть и выделим полный квадрат по переменной х:
. Теперь все слагаемые перенесем в левую часть и выделим полный квадрат по переменной х:  или
или  . Таким образом, заданная кривая – это нижняя дуга (
. Таким образом, заданная кривая – это нижняя дуга ( .
. ) и отрезком прямой x =0 (при
) и отрезком прямой x =0 (при  ). Поэтому ее разбиваем на две простые области
). Поэтому ее разбиваем на две простые области  . Тогда область
. Тогда область  . Область
. Область  . Применяя формулу (2) и третье свойство двойного интеграла (см. п.1.1), получаем:
. Применяя формулу (2) и третье свойство двойного интеграла (см. п.1.1), получаем:
 .
. Решение: Область D представлена на рис.11, из которого видно, что она не является простой ни в одном из направлений, поэтому ее необходимо разбить на простые области.
Решение: Область D представлена на рис.11, из которого видно, что она не является простой ни в одном из направлений, поэтому ее необходимо разбить на простые области. и у = х -4 при
и у = х -4 при 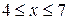 , которые пересекаются в точке (4,0). Верхняя граница так же состоит из двух частей - кубической параболы
, которые пересекаются в точке (4,0). Верхняя граница так же состоит из двух частей - кубической параболы  , которые пересекаются в точке (2,8). Через точки пересечения границ проводим координатные линии х =2 и х =4, которые разбивают D на три простые области
, которые пересекаются в точке (2,8). Через точки пересечения границ проводим координатные линии х =2 и х =4, которые разбивают D на три простые области  . В
. В  нижняя граница y =0, а верхняя
нижняя граница y =0, а верхняя  нижняя граница y =0, а верхняя – прямая у =10- х. В
нижняя граница y =0, а верхняя – прямая у =10- х. В  нижняя граница у = х -4, а верхняя - у =10- х. Расставляя пределы интегрирования для каждой из простых областей, получаем:
нижняя граница у = х -4, а верхняя - у =10- х. Расставляя пределы интегрирования для каждой из простых областей, получаем:
 левая граница описывается выражением
левая граница описывается выражением  , а правая - х = у +4. Во второй области при
, а правая - х = у +4. Во второй области при 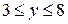 левая граница по-прежнему остается параболой
левая граница по-прежнему остается параболой 
 В качестве упражнения на расстановку пределов интегрирования рассмотрим задачу о перемене порядка интегрирования в повторном интеграле
В качестве упражнения на расстановку пределов интегрирования рассмотрим задачу о перемене порядка интегрирования в повторном интеграле  . Для ее решения необходимо построить область интегрирования D, которая находится в полосе между прямыми x = a, x = b и ограничена снизу линией
. Для ее решения необходимо построить область интегрирования D, которая находится в полосе между прямыми x = a, x = b и ограничена снизу линией  , только в этом случае область D проектируют на ось Oх.
, только в этом случае область D проектируют на ось Oх. .
. - дуга окружности
- дуга окружности  (рис.12). Проектируем область D на ось Оу, в результате получаем отрезок
(рис.12). Проектируем область D на ось Оу, в результате получаем отрезок  . Левой границей области является прямая х =0, правой - на участке [0,1] прямая х = у, а на участке
. Левой границей области является прямая х =0, правой - на участке [0,1] прямая х = у, а на участке  - дуга окружности
- дуга окружности . Поэтому область D разбиваем на две области
. Поэтому область D разбиваем на две области 
 .
. Решение: Для каждого из повторных интегралов построим свою область. Область
Решение: Для каждого из повторных интегралов построим свою область. Область  находится в полосе между прямыми y =0 и y =π и имеет левую границу х =-1 и правую границу х =cos y. Сумма этих двух областей и есть искомая область D, она изображена на рис.13. Спроектируем ее на ось Ох, получим отрезок [-1,1]. Относительно оси Ох область D является простой, ее нижней границей является прямая у = х -1, а верхней – у =arccos х.
находится в полосе между прямыми y =0 и y =π и имеет левую границу х =-1 и правую границу х =cos y. Сумма этих двух областей и есть искомая область D, она изображена на рис.13. Спроектируем ее на ось Ох, получим отрезок [-1,1]. Относительно оси Ох область D является простой, ее нижней границей является прямая у = х -1, а верхней – у =arccos х.



