
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
П.2.3. Вычисление тройного интеграла в сферических координатах.Содержание книги
Поиск на нашем сайте
Точка в трехмерном пространстве описывается тремя координатами (x, y, z) которые являются проекциями точки на оси Oх, Oу и Oz. Используем другой подход. Введем r - расстояние от начала координат до точки, j - угол поворота в плоскости Oxy, y - угол, который отсчитывают от плоскости Oxy. Сферические координаты (r,j,y) связаны с декартовыми координатами соотношениями
Сферические координаты удобно применять в случае, когда область интегрирования есть шар или его часть, так как уравнение его границы - сферы x 2+ y 2+ z 2= R 2, где R - радиус сферы, в сферических координатах имеет вид r = R. Удобно также переходить и в случае, если подынтегральная функция содержит выражения вида x 2+ y 2+ z 2= r ².Если область G ограничена эллипсоидом x 2/ a 2+ y 2/ b 2+ z 2/ с 2=1, то используют обобщенные сферические координаты
Пример 1: Вычислить Решение: Границей области G является сфера x 2+ y 2+ z 2=1, уравнение которой в сферических координатах имеет вид r =1. Так как r – расстояние до начала координат, то для любой точки шара выполняется неравенство
Пример 2: Вычислить
Рис.40 Решение: Область G приведена на рис. 40. Как уже говорилось, для всех точек шара справедливо
Рис.41 Решение: Преобразуем уравнение сферы к каноническому виду, выделив полный квадрат по z:
Пример 4: Перейти к сферическим координатам и вычислить
Решение: Область G - это часть шара, лежащего в первом октанте и вырезанного конусом (рис.42).Как уже говорилось, для шара в первом октанте Перейдем к сферическим координатам:
Рис.42 Рис.43
Пример 5: В интеграле
Решение: Область G приведена на рис.43. Из рисунка видно, что нижней границей области является сфера со смещенным центром, ее уравнение r =2 R sin ψ, а верхней – сфера с центром в начале координат, уравнение которой r = R. Поэтому область G необходимо разбить на две области конической поверхностью, проходящей через линию пересечения двух сфер. Найдем ее уравнение: 2 R sin ψ = R или sinψ=1/2, откуда получаем Замечание: При решении некоторых задач, например, связанных с радиолокацией, удобнее отсчитывать угол y не от плоскости Oху, а от оси Oz. Приведем данные координаты:
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 3258; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.219.213 (0.006 с.) |

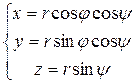 , где 0£j<2p, -p/2£y£p/2, 0£r<+¥. Якобиан перехода к сферическим координатам равен
, где 0£j<2p, -p/2£y£p/2, 0£r<+¥. Якобиан перехода к сферическим координатам равен  (проверить самостоятельно). Тогда справедлива формула замены в тройном интеграле:
(проверить самостоятельно). Тогда справедлива формула замены в тройном интеграле: (20)
(20) , где якобиан
, где якобиан  . В этих координатах уравнение эллипсоида имеет простой вид r =1.
. В этих координатах уравнение эллипсоида имеет простой вид r =1. , где G – шар
, где G – шар  .
. . Угол φ вводится в плоскости Oxy так же, как и в полярных координатах. Проекция шара на плоскость Oxy - круг, а для круга
. Угол φ вводится в плоскости Oxy так же, как и в полярных координатах. Проекция шара на плоскость Oxy - круг, а для круга  . Угол отклонения ψ от плоскости Oxy принимает наибольшее значение
. Угол отклонения ψ от плоскости Oxy принимает наибольшее значение  для точек, лежащих на оси Оz при z >0 и наименьшее значение
для точек, лежащих на оси Оz при z >0 и наименьшее значение  на оси Oz при z <0. Поэтому для шара всегда
на оси Oz при z <0. Поэтому для шара всегда  . Таким образом, при переходе к сферическим координатам шар G преобразуется в область Ω, которая является прямоугольным параллелепипедом:
. Таким образом, при переходе к сферическим координатам шар G преобразуется в область Ω, которая является прямоугольным параллелепипедом: 
 , где G – часть шара
, где G – часть шара 
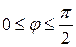 . Угол ψ принимает в данной области наименьшее значение ψ =0 для точек координатной плоскости z =0, а наибольшее значение
. Угол ψ принимает в данной области наименьшее значение ψ =0 для точек координатной плоскости z =0, а наибольшее значение 
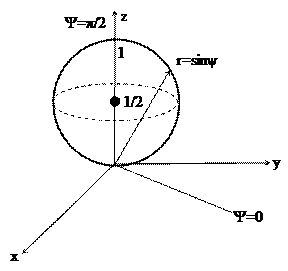 Пример 3: Вычислить тройной интеграл
Пример 3: Вычислить тройной интеграл 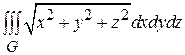 , если область G ограничена сферой
, если область G ограничена сферой 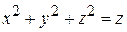 .
. . Сфера с центром в точке (0,0,1/2) радиуса 1/2, касается начала координат и расположена выше координатной плоскости z =0 (рис. 41). Ее уравнение в сферических координатах имеет вид r =sin ψ, так что для всех внутренних точек выполняется неравенство
. Сфера с центром в точке (0,0,1/2) радиуса 1/2, касается начала координат и расположена выше координатной плоскости z =0 (рис. 41). Ее уравнение в сферических координатах имеет вид r =sin ψ, так что для всех внутренних точек выполняется неравенство  . Так как проекцией области G на плоскость Оху является круг, то
. Так как проекцией области G на плоскость Оху является круг, то  . Расставляем пределы интегрирования:
. Расставляем пределы интегрирования:
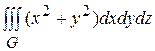 , где G - объем, ограниченный поверхностями x 2+ y 2= z 2, x 2+ y 2+ z 2= a 2, z =0, x =0, y =0
, где G - объем, ограниченный поверхностями x 2+ y 2= z 2, x 2+ y 2+ z 2= a 2, z =0, x =0, y =0 
 ,
,  .
.

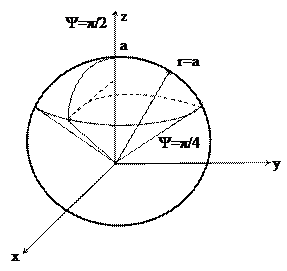
 перейти к сферическим координатам и расставить пределы интегрирования, если G – общая часть двух шаров
перейти к сферическим координатам и расставить пределы интегрирования, если G – общая часть двух шаров  и
и  .
. . В первой области при
. В первой области при  координата r изменяется от 0 до 2 R sin ψ, а во второй области при
координата r изменяется от 0 до 2 R sin ψ, а во второй области при  r изменяется от 0 до R. В обоих случаях
r изменяется от 0 до R. В обоих случаях 
 , где 0£j<2p, 0£y£p, 0£r<+¥,
, где 0£j<2p, 0£y£p, 0£r<+¥,  .
.


