
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приложения тройного интеграла. ⇐ ПредыдущаяСтр 7 из 7
1. Объем V тела G находится по формуле:
2. Масса m тела G с объемной плотностью ρ (х, у, z) вычисляется по формуле:
3.Статические моменты
4. Координаты центра тяжести тела G с массой m определяются по формулам:
5. Моменты инерции тела G относительно координатных плоскостей равны:
6. Моменты инерции
Для однородного тела ρ(x, y, z)=const и в некоторых задачах полагают ρ=1.
Пример 1: Вычислить объем тела, ограниченного эллипсоидом Решение: Для вычисления объема в тройном интеграле (21) перейдем к обобщенным сферическим координатам x = a cos φ cos ψ, y = b sin φ cos ψ, z = c sin ψ. Уравнение эллипсоида в них принимает вид r =1, а углы φ и ψ изменяются так же, как для шара. Область Ω является прямоугольным параллелепипедом
Пример 2: Найти координаты центра тяжести однородного тела, ограниченного параболоидом z =3- x ²- y ² и плоскостью z =0.
Рис.44 Решение:В силу симметрии тела относительно координатных плоскостей Оxz и Oyz (рис.44)
Вычисляем статический момент
и находим
Пример 3: Вычислить момент инерции однородного шара Решение:Поместим начало координат в центр шара. Тогда момент инерции шара относительно центра будет равен моменту инерции относительно начала координат, т.е. полярному моменту инерции. При вычислении тройного интеграла переходим к сферическим координатам.
2.6. Задачи для самостоятельного решения. 1. Вычислить тройной интеграл 2. Вычислить тройной интеграл 3. Перейти к новым координатам и вычислить интеграл 4. В интеграле
5. В интеграле 6. Вычислить 7. Вычислить 8. Вычислить интеграл 9. Вычислить 10. Вычислить 11. Вычислить интеграл 12. Вычислить объем тела, ограниченного цилиндрами z =4- y ² и z = y ²+2 и плоскостями х =-1, х =2. 13. Вычислить объем тела, ограниченного параболоидом z =6- x ²- y ² и конусом z ²= x ²+y². 14. Вычислить объем тела, ограниченного параболоидом 3 z = x ²+ y ² и сферой x 2+ y 2+ z 2=4 (внутренний по отношению к параболоиду). 15. Вычислить объем тела, ограниченного сферами x 2+ y 2+ z 2=1, x 2+ y 2+ z 2=16, конусом z ²= x ²+y² и плоскостями x =0, у =0, z =0 16. Найти массу и координаты центра тяжести шара x 2+ y 2+ z 2=2Rz, если плотность в каждой точке шара обратно пропорциональна расстоянию от нее до начала координат (т.е. 17. Вычислить координаты центра тяжести тела, ограниченного эллипсоидом 18. Найти моменты инерции относительно координатных плоскостей тела, ограниченного плоскостями 19.Найти полярный момент инерции однородного тела, ограниченного параболоидом z = x ²+ y ² и плоскостью z =4 (ρ =1). 20. Найти моменты инерции относительно координатных плоскостей тела, ограниченного конусом x ²=y²+ z ² и плоскостью x = h (h >0, ρ =1). Ответы Глава 1. 1. 6. 9. 12. 14. 20. 22. 23. 30.
Глава 2. 1. 18. Список литературы
1. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 1,2,3. М.: Наука. 1970.
2. Кудрявцев Л.Д. Курс математического анализа. М.: Высшая школа, 1981. 3. Демидович Б.П. Сборник задач и упражнений по математическому анализу. М.: АСТ Астрель, 2005. 4. Берман Г.Н. Сборник задач по курсу математического анализа. М.: Наука, 1969. 5. Сборник задач по курсу высшей математики. Под редакцией Г.И. Кручковича. Учебное пособие для вузов. М. «Высшая школа». 1973. 6. Сборник задач по высшей математике К.Н. Лунгу и др., под ред.С.Н. Федина. М.: Айрис-пресс. 2011.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 2755; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.255.127 (0.022 с.) |
 (21)
(21) (22)
(22) тела G относительно координатных плоскостей Оху, Oxz, Oyz соответственно равны:
тела G относительно координатных плоскостей Оху, Oxz, Oyz соответственно равны: (23)
(23)
 (24)
(24) относительно координатных осей Ох, Оу, Oz и полярный момент инерции
относительно координатных осей Ох, Оу, Oz и полярный момент инерции  относительно начала координат равны:
относительно начала координат равны: (25)
(25)
 ,
,  ,
,  :
:

 , осталось найти
, осталось найти  . Вначале вычислим массу m тела. Введем цилиндрические координаты: x = r cos φ, y = r sin φ, z = z и расставим пределы интегрирования в области G:
. Вначале вычислим массу m тела. Введем цилиндрические координаты: x = r cos φ, y = r sin φ, z = z и расставим пределы интегрирования в области G:
 :
:
 .
. радиуса 1 относительно его центра.
радиуса 1 относительно его центра.
 , где область G ограничена гиперболическим параболоидом z = xу и плоскостями у = х, x =1 и z =0.
, где область G ограничена гиперболическим параболоидом z = xу и плоскостями у = х, x =1 и z =0. , где область G ограничена цилиндром
, где область G ограничена цилиндром  и плоскостями у =0, z= 0 и
и плоскостями у =0, z= 0 и  .
. , где G расположена в первом октанте (x >0, y >0, z >0) и ограничена поверхностями
, где G расположена в первом октанте (x >0, y >0, z >0) и ограничена поверхностями  ,
,  , у = αx, у = βx, (0< a < b, 0< α < β, 0< m < n).
, у = αx, у = βx, (0< a < b, 0< α < β, 0< m < n). перейти к цилиндрическим координатам, если область G ограничена цилиндром x 2+ y 2= R ²и плоскостями z =0, z =1, y = x,
перейти к цилиндрическим координатам, если область G ограничена цилиндром x 2+ y 2= R ²и плоскостями z =0, z =1, y = x, 
 , где G - область, ограниченная верхней частью конуса x 2+ y 2= z ² и плоскостью z =1.
, где G - область, ограниченная верхней частью конуса x 2+ y 2= z ² и плоскостью z =1. , где область G ограничена параболоидом
, где область G ограничена параболоидом  и плоскостью z =3.
и плоскостью z =3. , переходя к цилиндрическим координатам.
, переходя к цилиндрическим координатам. , где G- область между сферами x 2+ y 2+ z 2= а ²и x 2+ y 2+ z 2= b ²(a < b).
, где G- область между сферами x 2+ y 2+ z 2= а ²и x 2+ y 2+ z 2= b ²(a < b). , где область G ограничена плоскостями x=0, y=0, z=0 и сферой x 2+ y 2+ z 2= а ².
, где область G ограничена плоскостями x=0, y=0, z=0 и сферой x 2+ y 2+ z 2= а ². , переходя к сферическим координатам.
, переходя к сферическим координатам. .
. , k – коэффициент пропорциональности).
, k – коэффициент пропорциональности). и плоскостями x =0, у =0, z =0
и плоскостями x =0, у =0, z =0  , x =0, у =0, z =0.
, x =0, у =0, z =0. . 2.
. 2.  . 3.
. 3.  . 4.
. 4. 
 . 5.
. 5. 
 . 7.
. 7. 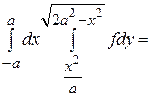
 . 8.
. 8.  .
. . 10.
. 10.  . 11.
. 11. 
 . 13.
. 13.  .
. . 15.
. 15.  . 16. -8. 17. 12. 18.
. 16. -8. 17. 12. 18.  . 19.
. 19.  .
. . 21.
. 21.  .
. .
. . 24.
. 24.  . 25. 24 π. 26.
. 25. 24 π. 26.  . 27.
. 27.  . 28.
. 28.  . 29.
. 29.  .
. . 31.
. 31.  . 32.
. 32.  . 33. 3 π. 34.
. 33. 3 π. 34.  . 35.
. 35.  . 36.
. 36.  . 37.
. 37.  . 38.
. 38.  . 39.
. 39.  . 40.
. 40.  . 41.
. 41.  . 42.
. 42.  ,
,  43.
43.  . 44.
. 44.  . 45.
. 45.  . 46.
. 46. 
 . 47.
. 47.  . 48.
. 48.  . 49.
. 49.  . 50.
. 50.  .
. . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  . 6.
. 6.  . 7.
. 7.  . 8.
. 8.  . 9.
. 9.  . 10.
. 10.  . 11.
. 11.  . 12. 8. 13.
. 12. 8. 13.  . 14.
. 14.  15.
15.  . 16.
. 16.  ,
,  . 17.
. 17.  .
. . 19.
. 19.  . 20.
. 20.  .
.


