
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Криволинейные координаты. Замена переменных в двойном интегралеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В ряде задач для упрощения вычисления двойного интеграла удобно выполнить замену переменных (перейти к новым, криволинейным координатам). Этот переход определяется видом области интегрирования и видом подынтегральной функции. В общем случае криволинейные координаты вводятся системой уравнений:
Тогда замена переменных в двойном интеграле производится по формуле:
где D* - образ области D в плоскости Функциональный определитель Наиболее употребительным примером криволинейных координат являются полярные координаты, которые связаны с декартовыми координатами соотношениями:
здесь Якобиан перехода в этом случае равен
и формула (3) записывается в виде
Если область интегрирования D* в полярной системе координат можно задать неравенствами:
Пример. Вычислить двойной интеграл
направлением оси Ох угол 4) x= 0 – прямая, совпадающая с осью Оy. Вычисления удобно провести в полярных координатах. Подставляя в уравнения границ области D 1)
2)
3) 4) При любом фиксированном Следовательно, область D в полярной системе координат можно задать неравенствами:
С учетом формулы (5) получаем:
Ответ: Тройной интеграл Пусть V замкнутая область в декартовой прямоугольной системе координат Oxyz и
которую назовем интегральной суммой. Определение. Предел последовательности интегральных сумм
т.е.
Теорема существования тройного интеграла. Если функция Свойства тройного интеграла аналогичны свойствам двойного интеграла. Отметим лишь, что если область
|
||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 1556; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.26.149 (0.005 с.) |

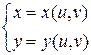 , где u, v – новые координаты.
, где u, v – новые координаты.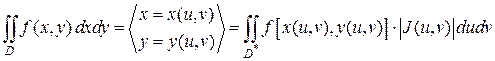 , (3)
, (3) при данном отображении
при данном отображении 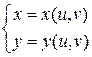 .
.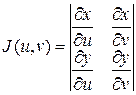 - называется якобианом перехода к криволинейным координатам (
- называется якобианом перехода к криволинейным координатам (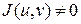 в области
в области  ).
). ,
,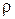 - полярный радиус (
- полярный радиус ( ) и
) и 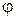 - полярный угол (
- полярный угол (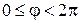 ).
).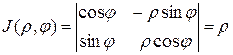 ,
,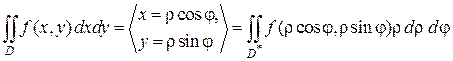 (4).
(4). Рис. 7
Рис. 7
 и при этом каждый луч, проходящий через внутренние точки области, пересекает границу не более чем в двух точках (Рис. 7), то имеет место формула:
и при этом каждый луч, проходящий через внутренние точки области, пересекает границу не более чем в двух точках (Рис. 7), то имеет место формула:
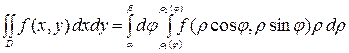 (5).
(5).
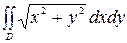 , где D:
, где D: 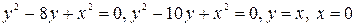 .
. Рис. 8
Рис. 8

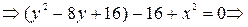
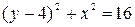 -
окружность с центром в точке (0,4) и радиусом 4
2)
-
окружность с центром в точке (0,4) и радиусом 4
2) 
 - окружность с центром в точке (0,5) и радиусом 5
3) y=x – прямая, проходящая через начало координат, образующая с положительным
- окружность с центром в точке (0,5) и радиусом 5
3) y=x – прямая, проходящая через начало координат, образующая с положительным
 .
.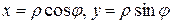 , получаем их полярные уравнения:
, получаем их полярные уравнения:
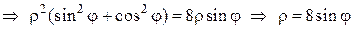 .
.
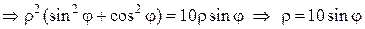 .
.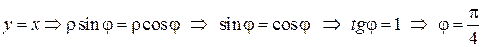 .
.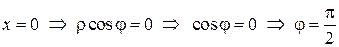 .
. луч, выходящий из начала координат пересекает границу области D в двух точках: в точке входа
луч, выходящий из начала координат пересекает границу области D в двух точках: в точке входа  , в которой
, в которой  и в точке выхода
и в точке выхода  , в которой
, в которой  .
.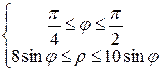


 непрерывная функция, определенная в этой области. Разобьем область V произвольным образом на n непересекающихся областей Vi с объемами
непрерывная функция, определенная в этой области. Разобьем область V произвольным образом на n непересекающихся областей Vi с объемами  . В каждой области Vi возьмем произвольным образом точку
. В каждой области Vi возьмем произвольным образом точку  и составим сумму
и составим сумму
 ,
, при
при  и стремлении к нулю максимального из диаметров частичных областей Vi, который не зависит от разбиения области
и стремлении к нулю максимального из диаметров частичных областей Vi, который не зависит от разбиения области  на частичные области Vi и выбора точек Mi, называется тройным интегралом от функции
на частичные области Vi и выбора точек Mi, называется тройным интегралом от функции  по области V и символически обозначается
по области V и символически обозначается ,
, .
. некоторой гладкой поверхностью, то
некоторой гладкой поверхностью, то .
.


