
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
А. Д. Романов, О. Д. АгибаловаСодержание книги
Поиск на нашем сайте
В г. Северодвинске А.Д. Романов, О.Д. Агибалова КРАТНЫЕ ИНТЕГРАЛЫ. ВЕКТОРНЫЙ АНАЛИЗ. Учебное пособие для студентов заочного отделения (I I I-й семестр) Северодвинск Севмашвтуз УДК 512 Оглавление Введение………………………………………………………………………….…4 1. Кратные интегралы……………………………………………………………....5 1.1. Двойной интеграл………………………………………………………………5 1.1.1. Свойства двойного интеграла……………………………………………5 1.1.2. Вычисление двойного интеграла………………………………………...6 1.1.3. Криволинейные координаты. Замена переменных в двойном интеграле…………………………………………………………………...8 1.2. Тройной интеграл……………………………………………………………...11 1.2.1. Вычисление тройных интегралов в декартовой системе координат…………………………………………………………………12 1.2.2. Криволинейные координаты в пространстве. Замена переменных в тройном интеграле……………………………………………………….13 1.3. Приложения двойных и тройных интегралов к задачам геометрии и физики………………………………………………………………………….17 1.3.1. Приложения двойных интегралов………………………………………17 1.3.2. Приложения тройных интегралов………………………………………19 2. Векторный анализ……………………………………………………………….22 2.1. Скалярное поле………………………………………………………………..22 2.2. Векторное поле………………………………………………………………..24 2.3. Криволинейные интегралы первого рода……………………………………26 2.4. Криволинейные интегралы второго рода……………………………………27 2.4.1. Независимость криволинейного интеграла второго рода от пути интегрирования……………………………………………………29 2.5. Поверхностные интегралы первого рода…………………………………… 30 2.6. Поверхностные интегралы второго рода……………………………………32 2.6.1. Связь поверхностных интегралов первого и второго рода……………33 2.7. Циркуляция и поток векторного поля………………………………………..35 2.8. Интегральные теоремы векторного анализа…………………………………36 3. Контрольная работа. Задания……………………………………………...37 3.1. Пример выполнения контрольной работы Вариант № 0……………...37 3.2. Варианты заданий контрольной работы ………………………………...42 Рекомендуемая литература………………………………………………………...49
ВВЕДЕНИЕ Данное пособие предназначено для студентов, обучающихся заочно. Пособие разработано в соответствии с требованиями Государственного образовательного стандарта данной специальности и содержит те разделы курса математики, которые изучаются, в соответствии с учебной программой, в третьем семестре. В пособии кратко изложены основные теоретические положения интегрального исчислений функций многих переменных, векторного анализа, приведено достаточное количество примеров решения задач. После самостоятельного изучения теоретического материала и приобретения навыков решения задач студенты должны выполнить две контрольные работы. Варианты заданий контрольных работ и примеры их выполнения также приведены в пособии. Следует отметить, что данное пособие должно рассматриваться лишь как основа для изучения, указанных выше, разделов математики. При самостоятельной работе следует обращаться и к другим источникам, перечень рекомендуемой учебной литературы приведен в конце пособия.
Кратные интегралы Двойной интеграл
Пусть D замкнутая область на плоскости
которую назовем интегральной суммой. Определение. Если существует конечный предел последовательности интегральных сумм
Теорема существования двойного интеграла. Если функция Геометрический смысл двойного интеграла.
В частности, если
Свойства двойного интеграла Будем считать, что все интегралы в перечисленных ниже утверждениях существуют. · Постоянный множитель можно выносить за знак двойного интеграла
· Если функции
· Свойство аддитивности. Если область
· Если функции
· Теорема о среднем для двойного интеграла. Если функции Тройной интеграл Пусть V замкнутая область в декартовой прямоугольной системе координат Oxyz и
которую назовем интегральной суммой. Определение. Предел последовательности интегральных сумм
т.е.
Теорема существования тройного интеграла. Если функция Свойства тройного интеграла аналогичны свойствам двойного интеграла. Отметим лишь, что если область
Векторный анализ Скалярное поле Определение. Если в каждой точке пространства или части пространства определено значение некоторой скалярной величины, то говорят, что задано скалярное поле этой величины. Пример скалярных полей дает поле температур, электростатическое поле. Задание скалярного поля осуществляется заданием скалярной функции точки
Если в пространстве введена декартова система координат
Геометрической характеристикой скалярного поля служат поверхности уровня (в случае плоского поля – линии уровня) – геометрическое место точек, в которых скалярная функция поля принимает одно и то же значение. Поверхность уровня данного поля определяется уравнением
Пример. Построить поверхности уровня скалярного поля Решение. Поверхности уровня определяются уравнением Пример 2. Найти линии уровня скалярного поля Решение. Линии уровня определяются уравнениями Дифференциальными характеристиками скалярного поля являются производная по направлению и градиент скалярного поля. Пусть Определение. Производная скалярного поля
Отметим еще раз, что в этой формуле Таким образом, производная скалярного поля по направлению характеризует скорость изменения поля в данном направлении, а сами частные производные Определение. Градиентом скалярного поля
Отметим свойства градиента и связь между производной поля по направлению и градиентом поля: · Производная поля
· Градиент направлен в сторону возрастания поля, направление градиента является направлением быстрейшего изменения поля. · Градиент скалярного поля в данной точке направлен по нормали к поверхности уровня поля, проходящей через эту точку. Пример 1. Найти производную поля Решение. Имеем Ответ:
Пример 2. Найти угол между градиентами поля Решение. Имеем Ответ: Векторное поле Определение. Если в каждой точке пространства или части пространства определена векторная величина Если в пространстве введена декартова система координат, то задание векторного поля
Геометрической характеристикой векторного поля является векторная линия. Определение. Векторной линией векторного поля Пусть векторное поле определяется вектором
где
- непрерывные функции от Тогда дифференциальные уравнения векторных линий имеют вид
Проинтегрировав эту систему дифференциальных уравнений можно получить уравнения векторных линий поля. Дифференциальными характеристиками векторного поля являются дивергенция и ротор векторного поля. Определение. Дивергенцией векторного поля
Точки Пример. Найти дивергенцию векторного поля Решение. Имеем Ответ: Определение. Ротором векторного поля
или в символической, удобной для запоминания, форме
Этот определитель обычно раскрывается по элементам первой строки, при этом операция умножения элементов второй строки на элементы третьей строки понимается как операция дифференцирования, например, Ротор (вихрь) векторного поля характеризует завихренность поля. Если в некоторой области Пример. Найти ротор векторного поля Решение. Имеем
Контрольная работа. Тема «Приложение кратных интегралов. Векторный анализ» Задания 1. Найти объём тела, ограниченного заданными поверхностями (таб. 1). 2. Найти угол между градиентами скалярных полей 3. Найти поток векторного поля 4. Найти циркуляцию векторного поля Пример выполнения контрольной работы. Вариант № 0 1. Найти объем тела, заданного ограничивающими его поверхностями.
Решение. Объем тела вычисляется по формулу:
Тело V ограничено снизу плоскостью Для вычисления интеграла удобно перейти к цилиндрическим координатам: Запишем уравнения границ в цилиндрических координатах: 1) 2)
Пределы изменения координат φ и ρ определяем по виду проекции области интегрирования V на плоскость xOy (Рис. 24). Пределы изменения угла φ будут от
Рис. 24 Таким образом,
Ответ: 2. Найти угол между градиентами скалярных полей Решение. Градиент скалярного поля
Находим частные производные функции
Аналогично, находим градиент поля
Напомним, что угол между векторами
Тогда:
Ответ: угол между градиентами скалярных полей 3. Найти поток векторного поля Решение. Если векторное поле
где V – тело, ограниченное замкнутой поверхностью S. Найдем дивергенцию поля, которая вычисляется по формуле:
В нашем случае имеем:
Тело V, границей которого является поверхность S, представляет собой треугольную пирамиду (Рис. 25) ограниченную координатными плоскостями и плоскостью
Рис. 25
Ответ: 4. Найти циркуляцию векторного поля Решение. Если линия задана параметрически, т. е.
В нашем случае
Подставляя эти выражения в формулу для вычисления циркуляции, получаем:
Ответ:
Варианты заданий контрольной работы Таблица 1. Варианты задания 1
Таблица 2. Варианты задания 2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 414; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.151.127 (0.01 с.) |

 в декартовой прямоугольной системе координат Oxy. Пусть z и z=f(x, y) – произвольная функция, определенная и непрерывная в этой области. Разобьем область D на n -непересекающихся областей Di
в декартовой прямоугольной системе координат Oxy. Пусть z и z=f(x, y) – произвольная функция, определенная и непрерывная в этой области. Разобьем область D на n -непересекающихся областей Di  , площади которых обозначим через
, площади которых обозначим через  . В каждой области Di возьмем произвольную точку Mi (xi, yi) и составим сумму
. В каждой области Di возьмем произвольную точку Mi (xi, yi) и составим сумму ,
, при
при  и стремлении к нулю максимального из диаметров частичных областей Di
и стремлении к нулю максимального из диаметров частичных областей Di  на частичные области Di и выбора точек Mi, то этот предел называется двойным интегралом от функции
на частичные области Di и выбора точек Mi, то этот предел называется двойным интегралом от функции  по области D и обозначается
по области D и обозначается , т.е.
, т.е. 
 непрерывна в области
непрерывна в области  существует.
существует. Рис. 1
Рис. 1
 в области
в области  (Рис.1), т.е.
(Рис.1), т.е.
 .
.
 , то двойной интеграл будет равен площади области D:
, то двойной интеграл будет равен площади области D: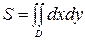 .
. , где
, где  .
. и
и  интегрируемы в области
интегрируемы в области  интегрируема в области
интегрируема в области  .
. и
и  , причем
, причем  , а
, а  - есть линия, их разделяющая (Рис. 2), то
- есть линия, их разделяющая (Рис. 2), то Рис. 2
Рис. 2

 и
и  непрерывны на области D и всюду в этой области
непрерывны на области D и всюду в этой области  , то
, то .
.
 и
и  , такая что справедлива формула
, такая что справедлива формула 
 непрерывная функция, определенная в этой области. Разобьем область V произвольным образом на n непересекающихся областей Vi с объемами
непрерывная функция, определенная в этой области. Разобьем область V произвольным образом на n непересекающихся областей Vi с объемами  . В каждой области Vi возьмем произвольным образом точку
. В каждой области Vi возьмем произвольным образом точку  и составим сумму
и составим сумму
 ,
, при
при  и стремлении к нулю максимального из диаметров частичных областей Vi, который не зависит от разбиения области
и стремлении к нулю максимального из диаметров частичных областей Vi, который не зависит от разбиения области  на частичные области Vi и выбора точек Mi, называется тройным интегралом от функции
на частичные области Vi и выбора точек Mi, называется тройным интегралом от функции  по области V и символически обозначается
по области V и символически обозначается ,
, .
.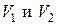 некоторой гладкой поверхностью, то
некоторой гладкой поверхностью, то .
.
 .
. , то
, то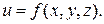

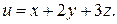
 где
где 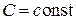 . Это есть однопараметрическое семейство параллельных плоскостей.
. Это есть однопараметрическое семейство параллельных плоскостей.
 При
При 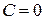 получаем пару прямых
получаем пару прямых  . При
. При  получаем семейство гипербол.
получаем семейство гипербол. - единичный вектор данного направления
- единичный вектор данного направления  . Обозначим
. Обозначим  - приращение скалярного поля
- приращение скалярного поля  в точке
в точке 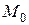 по направлению вектора
по направлению вектора  одинаково направлен с вектором
одинаково направлен с вектором  .
. , определяется соотношением
, определяется соотношением
 - направляющие косинусы вектора
- направляющие косинусы вектора  характеризуют скорость изменения поля по направлениям координатных осей. Если
характеризуют скорость изменения поля по направлениям координатных осей. Если  , то поле возрастает в направлении вектора
, то поле возрастает в направлении вектора  , то убывает.
, то убывает. , называется вектор, определяемый формулой
, называется вектор, определяемый формулой
 по направлению
по направлению  .
. в точке
в точке  по направлению вектора
по направлению вектора  .
. , его длина -
, его длина -  . Направляющие косинусы:
. Направляющие косинусы:  ,
,  ,
,  . Далее
. Далее  ,
,  ,
,  , тогда
, тогда  (
(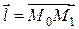 ).
). , поле убывает в данном направлении.
, поле убывает в данном направлении. в точках
в точках  и
и 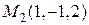 .
.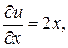
 ,
, 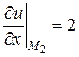 ;
;  ,
,  ,
, 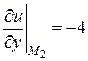 ;
;  ,
,  ,
,  . Обозначим искомый угол через
. Обозначим искомый угол через 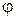 , тогда:
, тогда:  ,
,  и
и 
 .
. .
. , то говорят, что задано векторное поле.
, то говорят, что задано векторное поле. , так что
, так что
 называется кривая, в каждой точке
называется кривая, в каждой точке 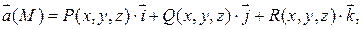

 , имеющие частные производные первого порядка.
, имеющие частные производные первого порядка.
 называется скалярная величина, обозначаемая символом
называется скалярная величина, обозначаемая символом  , и определяемая формулой
, и определяемая формулой
 , в которых
, в которых  , называются источниками, а точки, в которых
, называются источниками, а точки, в которых 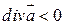 , называются стоками векторного поля. Таким образом, дивергенция векторного поля характеризует распределение источников и стоков поля.
, называются стоками векторного поля. Таким образом, дивергенция векторного поля характеризует распределение источников и стоков поля. в точке
в точке 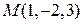 .
. ,
,  ,
,  . Подставляя найденные значения частных производных в формулу для вычисления дивергенции, получим
. Подставляя найденные значения частных производных в формулу для вычисления дивергенции, получим 
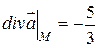 .
. и определяемый равенством
и определяемый равенством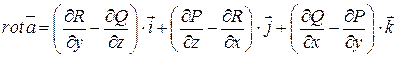

 .
. имеем
имеем  , то поле вектора
, то поле вектора 
 Ответ:
Ответ:  .
. и
и  в точке
в точке  (нормаль внешняя) (таб. 3).
(нормаль внешняя) (таб. 3).

 , сверху параболическим цилиндром
, сверху параболическим цилиндром  , боковая поверхность - круговой цилиндр с центром в точке
, боковая поверхность - круговой цилиндр с центром в точке  и радиусом 1,
и радиусом 1,  .
. .
. ;
;
 .
.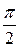 до
до  . При любом фиксированном угле φ, полярный радиус ρ изменяется от 0 до
. При любом фиксированном угле φ, полярный радиус ρ изменяется от 0 до  (уравнение окружности). При каждом значении (φ,ρ) в области D значение координаты z для области V меняются от
(уравнение окружности). При каждом значении (φ,ρ) в области D значение координаты z для области V меняются от  до
до  .
.


 .
. и
и  в точке
в точке  .
. в данной точке
в данной точке 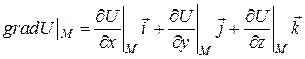 .
. :
: ,
,  ,
, 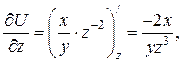
 ,
,  ,
,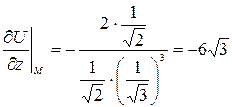 . Таким образом,
. Таким образом,  .
. в точке
в точке  ,
,  ,
,  .
.  ,
,  ,
, 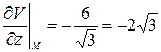 .
.  .
. и
и 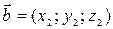 находится по формуле
находится по формуле .
. и
и  .
.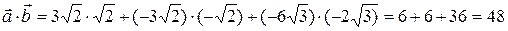 .
. .
. . Получаем:
. Получаем: 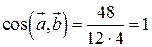 , то есть угол между градиентами равен нулю.
, то есть угол между градиентами равен нулю. и
и 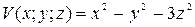 в точке
в точке  через внешнюю сторону замкнутой поверхности
через внешнюю сторону замкнутой поверхности  .
. непрерывно дифференцируемо внутри замкнутой поверхности
непрерывно дифференцируемо внутри замкнутой поверхности  , то можно использовать формулу Гаусса – Остроградского для вычисления потока в направлении внешней нормали:
, то можно использовать формулу Гаусса – Остроградского для вычисления потока в направлении внешней нормали: ,
, .
. ;
;  ;
;  .
. ,
,  ,
,  . Следовательно,
. Следовательно,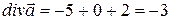 .
. (
( ).
).




 .
. вдоль замкнутого контура
вдоль замкнутого контура  (в направлении, соответствующем возрастанию параметра
(в направлении, соответствующем возрастанию параметра 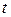 ).
). ,
,  , то циркуляция поля
, то циркуляция поля  равна:
равна:
 ,
, 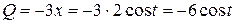 ,
,  .
. ,
,  ,
,  .
.
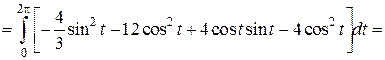




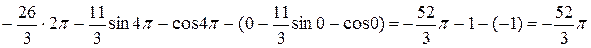 .
. .
. ,
,  ,
, 
 ,
, 
 ,
,  ,
,  ,
, 
 ,
, 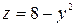 ,
,  ,
,  ,
,  ,
, 
 ,
, 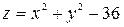 ,
,  ,
,  ,
, 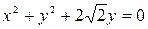 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 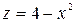 ,
,  ,
,  ,
,  ,
, 
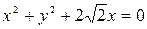 ,
,  ,
,  ,
,  ,
, 

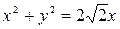 ,
,  ,
, 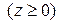
 ,
,  , z=0
, z=0
 ,
, 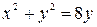 ,
, 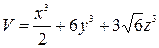 ,
,  ,
, 
 ,
, 


