Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Криволинейные координаты в пространстве. Замена переменных в тройном интегралеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Так же, как и в случае двойного интеграла при вычислении тройных интегралов в ряде задач для упрощения вычислений, оказывается удобным произвести замену переменных (или перейти к криволинейным координатам). Выбор новых координат определяется в первую очередь видом области интегрирования. В общем случае криволинейные координаты вводятся системой
Тогда замена переменных в тройном интеграле осуществляется по формуле
где V* - образ области V при данном отображении.
Наиболее употребительными из криволинейных координат в пространстве являются: · Цилиндрические координаты. В случае цилиндрических координат положение точки M в пространстве определяется тремя числами
Якобиан перехода к цилиндрическим координатам есть
где V* образ области · Сферические координаты. В случае сферических координат положение точки M в пространстве определяется тремя числами
Якобиан перехода к сферическим координатам есть
где V* - образ области Замечание 1. При расстановке пределов в цилиндрических координатах внешний интеграл берут, как правило, по j, следующий за ним по r и внутренний по z. Замечание 2. При расстановке пределов интегрирования в сферических координатах внешний интеграл берут, как правило, по j, следующий за ним по q и внутренний по радиус-вектору r. Пример 1. Вычислить Решение. Область интегрирования V (Рис. 14) ограничена сверху плоскостью z=4, снизу параболоидом вращения Так как проекцией области V на плоскость xOy является круг
Уравнение параболоида в цилиндрических координатах будет Таким образом,
Ответ: Пример 2. Вычислить Решение. Поверхность
Для вычисления интеграла целесообразно перейти к сферическим координатам
Тогда уравнение сферы примет вид
φ будут от 0 до 2π. При каждом Таким образом,
Ответ:
|
||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 792; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.167.229 (0.009 с.) |

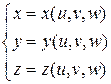 .
. , (8)
, (8) - якобиан перехода к криволинейным координатам (
- якобиан перехода к криволинейным координатам ( в области
в области  ).
). (Рис. 12):
(Рис. 12): Рис. 12
Рис. 12
 , где M1 – проекция точки M на плоскость xOy,
j (полярный угол) – угол между осью Ox и вектором
, где M1 – проекция точки M на плоскость xOy,
j (полярный угол) – угол между осью Ox и вектором  , (9)
, (9)
 .
.
 ,
, (10),
(10), (Рис. 13):
(Рис. 13): Рис. 13
Рис. 13
 ,
j – угол между осью Ox и вектором
,
j – угол между осью Ox и вектором  – угол между осью
– угол между осью  и вектором
и вектором 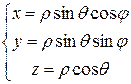 , (11)
, (11)
 .
.
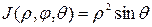 . Тогда формула перехода в тройном интеграле к сферическим координатам будет
. Тогда формула перехода в тройном интеграле к сферическим координатам будет (12),
(12), , где V область, ограниченная поверхностями:
, где V область, ограниченная поверхностями:  .
.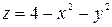 с вершиной в точке (0,0,4) и боковая поверхность есть круговой цилиндр
с вершиной в точке (0,0,4) и боковая поверхность есть круговой цилиндр  .
. (Рис. 15), то при вычислении тройного интеграла целесообразно перейти к цилиндрическим координатам:
(Рис. 15), то при вычислении тройного интеграла целесообразно перейти к цилиндрическим координатам: 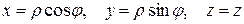 .
.
 (так как
(так как  ). Подынтегральная функция -
). Подынтегральная функция -  . Предельные изменения координат φ и ρ определяем по виду проекции области интегрирования V на плоскость xOy (Рис.15). Очевидно, что изменение угла φ будет от 0 до 2π. При любом фиксированном угле φ полярный радиус ρ изменяется от 0 до 2. Любая прямая, проходящая через проекцию D, параллельно оси Oz, пересекает область интегрирования V в двух точках: в точке входа
. Предельные изменения координат φ и ρ определяем по виду проекции области интегрирования V на плоскость xOy (Рис.15). Очевидно, что изменение угла φ будет от 0 до 2π. При любом фиксированном угле φ полярный радиус ρ изменяется от 0 до 2. Любая прямая, проходящая через проекцию D, параллельно оси Oz, пересекает область интегрирования V в двух точках: в точке входа  при
при  и в точке выхода
и в точке выхода  - при
- при 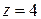 .
.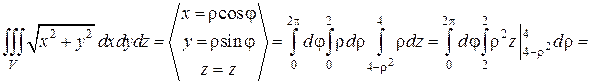


 , где
, где  .
. представляет собой сферу с центром в точке
представляет собой сферу с центром в точке  и радиусом
и радиусом  (Рис. 16), т.к.
(Рис. 16), т.к. .
. .
. .
. Рис. 16
Рис. 16

 .
Определим пределы изменения сферических координат φ, ρ, θ.
Пусть М произвольная точка области V. Угол φ – это угол между проекцией радиус-вектора
.
Определим пределы изменения сферических координат φ, ρ, θ.
Пусть М произвольная точка области V. Угол φ – это угол между проекцией радиус-вектора  угол θ (угол между радиус-вектором
угол θ (угол между радиус-вектором 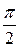 . При любых φ и θ, из указанной области, ρ изменяется от 0 до
. При любых φ и θ, из указанной области, ρ изменяется от 0 до  (уравнение сферы).
(уравнение сферы).