
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Получение формулы интеграла МораСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим балку, изображенную на рис. 15.6, а. Обозначим Введем в рассмотрение вспомогательную балку (та же балка, но нагруженная только единичной силой либо единичным изгибающим моментом). Нагрузим ее только одной силой Внутренние усилия, возникающие во вспомогательной балке, обозначим Воспользуемся теперь теоремой о взаимности работ, согласно которой работа внешних сил, приложенных к вспомогательной балке на соответствующих перемещениях заданной балки равна взятой с обратным знаком работе внутренних сил заданной балки на соответствующих перемещениях вспомогательной балки. Тогда При определении перемещений в балке, как правило, можно пренебрегать влиянием поперечной силы, (не учитывать второе слагаемое). Тогда, учитывая, что Определение перемещений по формуле интеграла Мора часто называют определением перемещений методом Мора, а саму формулу – интегралом Мора. Входящие в интеграл Мора изгибающие моменты берутся в произвольном поперечном сечении и поэтому представляют собой аналитические функции от текущей координаты z. Заметим, что если мы хотим в этой же точке K определить угол поворота поперечного сечения (
Правило Верещагина Недостатком метода Мора является необходимость получать значения внутренних силовых факторов, входящих в подинтегральные выражения формул (2.18) и (2.19), в общем виде, как функций от z, что становится достаточно трудоемким уже при двух – трех участках разбиения в балках и особенно – в рамах. Оказывается, что от этого недостатка можно уйти, если непосредственное интегрирование в формулах Мора заменить так называемым перемножением эпюр. Такая замена возможна в тех случаях, когда хотя бы одна из перемножаемых эпюр является прямолинейной. Этому условию соответствуют все системы, состоящие из прямолинейных стержней. Действительно, в таких системах эпюра, построенная от обобщенной единичной силы, всегда будет прямолинейной.
Способ вычисления интеграла Мора путем замены непосредственного интегрирования перемножением соответствующих эпюр называется способом (или правилом) Верещагина и заключается в следующем: чтобы перемножить две эпюры, из которых хотя бы одна является прямолинейной, нужно площадь одной эпюры (если есть криволинейная эпюра, то обязательно ее площадь) умножить на ординату другой эпюры, расположенную под центром тяжести первой.
17.6. Способ Верещагина При исследовании изгиба стержневых систем оказывается удобным для определения пе- ремещений использовать графо-аналитический метод, предложенный А. Н. Верещаги- ным (1924). Так как при определении линейных или угловых перемещений единичная на- грузка будет представлять собой либо силу, либо момент, то эпюра внутрен- него изгибающего момента для единичной системы всегда будет ограничена прямыми линиями. В этом случае интеграл Мора можно вычислить следую- щим образом. Пусть «грузовая» эпюра MP имеет криволиней- ное очертание, а «единичная» эпюра M1 пред- ставляет собой наклонную прямую (с углом наклона α). На «грузовой» эпюре MP на рас- стоянии x от начала координат выделим эле- мент шириной dx. Площадь этого элемента, очевидно, равна dA=MP·dx. «Единичный» мо- мент M1, соответствующий координате x, мож- но найти через тангенс угла α: 1 M x = ⋅ α tg. Запишем теперь интеграл Мора и подставим в него найденные соотношения: 1 MP ⋅ ⋅ M dx = dA⋅ x ⋅ tg α =tg α⋅ x ⋅ dA ∫ ∫ ∫. (17.9) Выражение под знаком последнего интеграла есть ничто иное, как статиче- ский момент «грузовой» эпюры относительно оси Oy ∫ Sy = x ⋅ dA. С другой стороны, статический момент можно найти как произведение пло- щади на координату центра тяжести «грузовой» эпюры Sy = xC ⋅ A. В этом случае интеграл (17.9) можно переписать так: 1 M M P C ⋅ ⋅ = dx A⋅ x ⋅ tg ∫ α. Произведение tg Cx ⋅ α представляет собой величину единичного момента в точке с координатой xC: 26 1 tg M x C = C ⋅ α. Таким образом, выражение для определения перемещения балки при изгибе по методу Верещагина запишем в следующем виде: ∑ ⋅ ⋅ ∆ = n E J A M C ос 1, (17.10) где А – площадь «грузовой» эпюры MP на данном участке; – величина «единичного» момента под центром тяжести «грузовой» эпюры на данном участке. M1C Для удобства использования выражения (17.10) запишем формулы для определения площади и координаты центра тяжести для некоторых характерных эпюр: а) прямоугольник – А=h·l, xC=l/2; б) треугольник – А=h·l/2, xC=l/3; в) вогнутая парабола – А=h·l/3, xC=l/4; г) выпуклая парабола – А=2·h·l/3, xC=3·l/8; д) полная парабола – А=2·h·l/3, xC=l/2. В качестве примера рассмотрим консольную балку длиной l, нагру- женную на конце силой F. Определим прогиб свободного края балки. Проанализируем две системы грузо- вую, – нагруженную только силой F, и единичную, – нагруженную единичной силой в направлении искомого пере- мещения. Построим для каждой из систем эпюру внутреннего изгибающего момента (MP и M1). Площадь «грузовой» эпюры найдем как A=F·l·l/2. Значение «единичного» момента под центром тяжести «грузовой» эпюры определим из пропорции 2 3. 1 M l C = ⋅ Тогда искомое перемещение z A z E J F l y E J F l ⋅ ⋅ ⋅ ⇒ = ⋅ ⋅ ⋅ 3 3 3 z E J A M C = ⋅ ⋅ ∆ = 3 1. Знак «плюс» показывает, что направление перемещения совпадает с направлением единичной силы
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1115; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.142.2 (0.012 с.) |

 и
и  , соответственно, изгибающий момент и поперечную силу, возникающие в заданной балке от действующей на нее группы нагрузок P. Пусть требуется определить прогиб балки (
, соответственно, изгибающий момент и поперечную силу, возникающие в заданной балке от действующей на нее группы нагрузок P. Пусть требуется определить прогиб балки ( ) в точке K.
) в точке K. (рис. 15.6, б). Единичную силу приложим в точке K, где нужно определить прогиб.
(рис. 15.6, б). Единичную силу приложим в точке K, где нужно определить прогиб.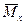 и
и  .
. .
.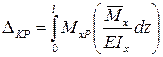 .
. ), то нам необходимо к вспомогательной балке приложить не единичную силу, а единичный момент
), то нам необходимо к вспомогательной балке приложить не единичную силу, а единичный момент  (рис. 15.6, в).
(рис. 15.6, в). соответствует единичной нагрузке и является линейной.
соответствует единичной нагрузке и является линейной. Подставим значения
Подставим значения 
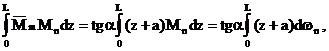
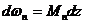 - дифференциал площади
- дифференциал площади  эпюры Mn.
эпюры Mn. Рис. 28
Рис. 28 представляет собой статический момент площади
представляет собой статический момент площади  относительно оси О – О1, при этом:
относительно оси О – О1, при этом:

 получим:
получим: (2.20)
(2.20)
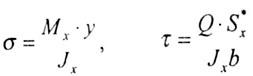



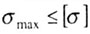
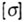 - допускаемое напряжение.
- допускаемое напряжение.

 зонах поперечного сечения и путем сравнения их с соответствующими допускаемыми напряжениями при растяжении
зонах поперечного сечения и путем сравнения их с соответствующими допускаемыми напряжениями при растяжении  и сжатии
и сжатии  :
:




