
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статически неопределимые задачиСодержание книги
Поиск на нашем сайте
Иногда в практике расчета конструкций требуется определить неизвестные силовые факторы (например, реакции связей или внутренние силы), при этом количество неизвестных силовых факторов превышает количество возможных уравнений равновесия для данной конструкции, и расчет произвести рассмотренными ранее способами не представляется возможным. Задачи на расчет конструкций, в которых внутренние силовые факторы не могут быть определены с помощью одних лишь уравнений равновесия статики, называют статически неопределимыми. Подобные задачи нередко встречаются при расчете конструкций, подверженных температурным деформациям. Рассмотрим невесомый стержень постоянного сечения площадью А, длиной l, жестко защемленный по концам (см. рис. 2). Составим для стержня уравнение равновесия: Σ Z = 0; RС- RВ= 0, откуда следует, что реакции RС и RВ равны между собой, а применив метод сечений установим, что продольная сила N в сечениях стержня равна неизвестным реакциям: N = RС= RВ. Составим дополнительное уравнение, для чего мысленно отбросим правую заделку и заменим ее реакцией RВ, тогда дополнительное уравнение деформации будет иметь вид: Δlt= ΔlСВ т. е. температурное удлинение стержня равно его укорочению под действием реакции RB, так как связи предполагаются абсолютно жесткими. Температурное удлинение стержня определяется по формуле: Δlt= αtl, где α - коэффициент линейного расширения стержня. Укорочение стержня под действием реакции: ΔlСВ= RBl / (EА). Приравняв правые части равенств, получим: αtl = RBl / (EА), откуда RB= αtEА. Температурные напряжения в реальных конструкциях могут достигать значительных величин. Чтобы исключить их отрицательное влияние на прочность конструкций, прибегают к различным методам. Мосты, например, закрепляют лишь на одном конце (на одном берегу), а второй конец оставляют подвижным. ***
Построение эпюр крутящих моментов Для наглядного изображения распределения крутящих моментов вдоль оси бруса строят эпюры крутящих моментов - графическое отображение величины крутящих моментов на каждом участке бруса. Крутящий момент в сечениях бруса определяется с помощью метода сечения. Так как равномерно вращающийся или неподвижный вал находится в равновесии, очевидно, что внутренние силы, возникающие в поперечном сечении, должны уравновешивать внешние моменты, действующие на рассматриваемую часть бруса. Отсюда следует, что крутящий момент в любом поперечном сечении численно равен алгебраической сумме внешних моментов, приложенных к брусу справа или слева от сечения. Эпюры крутящих моментов дают возможность определить опасное сечение. В частности, если брус имеет постоянное поперечное сечение по всей длине, то опасными будут сечения на участке, где возникает наибольший крутящий момент. Следует очень внимательно отнестись к определению знаков крутящего момента. Крутящий момент считается положительным, если при взгляде со стороны сечения результирующий момент внешних пар сил, приложенных к рассматриваемой части бруса, будет направлен против часовой стрелки, и наоборот (это положение условно и принимается для облегчения проверки расчетов, выполненных несколькими исполнителями). Рассматривая величины крутящих моментов, действующих в каждом конкретном сечении бруса, полагаем, что в сечении, где приложен вращающий (скручивающий) момент, значения крутящего момента изменяются скачкообразно (принцип смягченных граничных условий). ***
Пример построения эпюры крутящих моментов Силовая передача (трансмиссия), изображенная на рис. 2 состоит из вала, на котором размещены три шестерни - одна ведущая (А) и две ведомые (В и С). Решение Очевидно, что свободные концы вала, (вращающиеся в подшипниках) не подвержены действию вращающих моментов, т. е. крутящие моменты на участках 1 и 4 равны нулю. К шестерне В приложен вращающий момент 120 Нм, который направлен в противоположную сторону от ведущего скручивающего момента, приложенного к шестерне А. Следовательно крутящий момент на участке 3 будет равен разности крутящих моментов, приложенных к шестерням А и В. На эпюре это отобразится в виде ступени величиной 120 Нм, расположенной напротив сечения, где размещена шестерня В. К шестерне С приложен вращающий момент 180 Нм, направление которого противоположно моменту, приложенному к ведущей шестерне А, поэтому, начиная с сечения под шестерней С, крутящий момент будет равен разнице между скручивающим моментом шестерни А и моментами, приложенными к шестерням В и С, т. е.
Построив эпюру крутящих моментов, действующих в сечениях вала данной силовой передачи как показано на рис. 2, отмечаем, что максимальной величины - 300 Нм крутящий момент достигает на участке 2, т. е. этот участок и является критическим (наименее надежным). Теперь попробуем изменить расположение шестерен на валу, разместив ведущую шестерню А между ведомыми шестернями В и С, как показано на рис. 3. Приложенные к шестерням вращающие моменты оставим без изменения и построим эпюру крутящих моментов для измененной конструкции (рис. 3). Из полученной эпюры видно, что на участке 2 (между шестернями В и А) крутящий момент равен - 120 Нм, на участке 3 — + 180 Нм, а на участках 1 и 4 крутящие моменты равны нулю, как и в предыдущей конструкции. И если в рассмотренной ранее конструкции максимальный крутящий момент достигал 300 Нм, то теперь его величина снизилась до 180 Нм.
|
||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 480; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.94.189 (0.007 с.) |

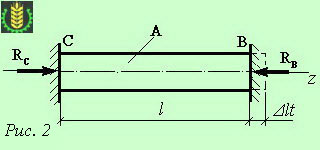 При нагревании в стержне возникают температурные напряжения сжатия.
При нагревании в стержне возникают температурные напряжения сжатия. 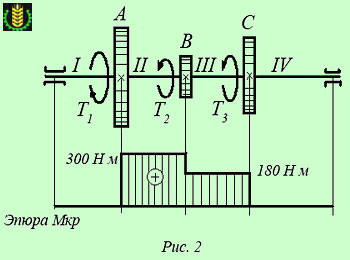 К шестерням приложены вращающие моменты: РА= 300 Нм, РВ= 120 Нм, РС= 180 Нм.
К шестерням приложены вращающие моменты: РА= 300 Нм, РВ= 120 Нм, РС= 180 Нм. 



