
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Передаточные отношения рядовых и многоступенчатых передач.Содержание книги
Поиск на нашем сайте
Деление передач на рядовые и ступенчатые имеет смысл, когда они содержат более двух подвижных звеньев. На рис. 17, а, б показаны примеры рядовой и ступенчатой передач, соответственно. Колёса рядовой передачи располагаются в одной плоскости или, иначе, в один ряд, отсюда и происходит название. В ступенчатой передаче каждая пара зацепляющихся колёс располагается в своей плоскости, образует свою ступень. На виде б): 1, 2 - первая ступень; 3, 4 - вторая. В рядовой передаче каждое звено содержит только одно зубчатое колесо. Номер звена и номер колеса совпадают. В ступенчатой передаче колёса 2 и 3 располагаются на одной ступени (одном валу), поэтому иногда они обозначаются номером вала, на котором они располагаются, и различаются по индексу, например 2′, 2′′ или 2а, 2б. Номер звена не проставляется, так как содержится в обозначениях колёс. Рядовая и ступенчатая передачи образуют класс передач с неподвижными осями колёс. Для любой такой передачи передаточное отношение от первого звена к последнему, n -му,равно произведению промежуточных передаточных отношений. Это правило выражается формулой u1,n = u1,2u2,3... un-1,n, (12) где индексы указывают номера звеньев. Для доказательства справедливости формулы представим каждое u в виде отношения скоростей: ω1 = ω1ω2 L ωn − 1. ωn ω2ω3ωn После сокращений уравнение обращается в тождество, что и доказывает справедливость формулы (12). Формула справедлива для любой последовательной цепи механизмов. При этом uij (здесь и далее запятую опускаем) есть передаточное отношение отдельного механизма. Применим формулу (12) к передачам, изображённым выше. Для рядовой передачи
Для ступенчатой передачи
Результаты показывают, что передаточное отношение рядовой передачи зависит от чисел зубьев только крайних колёс. Ступенчатая передача не обладает таким свойством. Знак «минус» в передаточном отношении u14 показывает, что колёса 1, 4 вращаются в разные стороны. 11. Дифференциальные и планетарные передачи. Формула Виллиса. Сложные зубчатые механизмы, в которых ось хотя бы одного колеса подвижна, называются планетарными механизмами. Планетарные механизмы подразделяются на планетарные редукторы и мультипликаторы, которые обладают одной степенью свободы и обязательно имеют опорное звено, и зубчатые дифференциальные механизмы, число степеней свободы которых два и более, и которые опорного звена обычно не имеют. К типовым планетарным механизмам относятся: · однорядный планетарный механизм со смешанным зацеплением (механизм Джеймса); · двухрядный планетарный механизм со смешанным зацеплением; · двухрядный планетарный механизм с двумя внешними зацеплениями; · двухрядный планетарный механизм с двумя внутренними зацеплениями. Элементы планетарного механизма имеют специальные названия: · зубчатое колесо с внешними зубьями, расположенное в центре механизма называется "солнечным"; · колесо с внутренними зубьями называют "короной" или "эпициклом"; · колеса, оси которых подвижны, называют "сателлитами"; · подвижное звено, на котором установлены сателлиты, называют «водило». Это звено принято обозначать не цифрой, а латинской буквой h. При вращении солнечного колеса сателлиты поворачиваются как рычаг относительно мгновенного центра вращения (опорное колесо неподвижно) и заставляют вращаться водило. При этом планетарные колеса (сателлиты) совершают сложное движение: вращаются вокруг собственной оси (относительно водила) с угловой скоростью Обычно у реального механизма имеется несколько симметрично расположенных блоков сателлитов Если в рассмотренном механизме освободить от закрепления опорное колесо (корпус редуктора) и сообщить ему вращение, то все центральные колеса станут подвижными и механизм превратится в дифференциальный, так как число степеней свободы его будет равно двум. Таким образом, дифференциальный механизм – это планетарный механизм с числом степеней свободы Число степеней свободы (подвижности) механизма показывает, скольким звеньям дифференциала необходимо сообщить независимые движения, чтобы получить определенность движения всех остальных звеньев. Здесь в зависимости от направления вращения наружных валов может происходить либо разложение движения (одного ведущего на два ведомых), либо сложение движения. Ведущим считается такой вал, у которого направление скорости вращения и момента совпадают. Следовательно, планетарный редуктор (или мультипликатор), имеющий неподвижное колесо, можно превратить в дифференциал, если освободить неподвижное (опорное) колесо и сообщить ему вращение. Наоборот, любой дифференциал можно превратить в планетарный редуктор, если закрепить одно (при W = 2) или несколько из его центральных колес. Это так называемое свойство обратимости планетарных механизмов, которое позволяет применять одинаковые методы исследования и проектирования для редукторов и для дифференциалов. При этом каждому элементарному дифференциалу будут соответствовать два планетарных редуктора В таблице приведены структурные схемы типовых планетарных механизмов, а также диапазоны рекомендуемых передаточных отношений и ориентировочные значения КПД при этих передаточных отношениях. Типовые планетарные механизмы
Формула Виллиса Формула Виллиса выводится на основании основной теоремы зацепления и устанавливает соотношение между угловыми скоростями зубчатых колес в планетарном механизме. Рассмотрим простейший планетарный механизм с одним внешним и одним внутренним зацеплением. Всему механизму сообщается угловая скорость равная по величине и противоположна по направлению угловой скорости водила, при этом водило остановится, а опорное колесо начнет поворачиваться. Таким образом, планетарный механизм превратится в механизм с неподвижными осями, состоящий из нескольких последовательно соединенных зубчатых колес. Такой механизм носит название обращенного механизма. Угловые скорости звеньев в каждом из рассматриваемых движений приведены в таблице
В движении звеньев относительно водила угловые скорости звеньев равны угловым скоростям в движении относительно стойки минус угловая скорость водила. Если в движении относительно стойки ось сателлита подвижна, то в движении относительно водила оси обоих зубчатых колес неподвижны. Поэтому к движению относительно водила можно применить основную теорему зацепления. Передаточное отношение обращенного механизма Передаточное отношение планетарного редуктора от любого колеса к водилу равно единице минус передаточное отношение обращенного механизма от этого колеса к опорному.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1368; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.133.251 (0.009 с.) |


 и вместе с водилом обкатываются вокруг его оси (переносное движение). Число степеней свободы этого механизма равно единице. Поэтому редуктор имеет постоянное передаточное отношение.
и вместе с водилом обкатываются вокруг его оси (переносное движение). Число степеней свободы этого механизма равно единице. Поэтому редуктор имеет постоянное передаточное отношение. . Их вводят с целью уменьшения габаритов механизма, снижения усилия в зацеплении, разгрузки подшипников центральных колес, улучшения уравновешивания водила, хотя механизм в этом случае имеет избыточные связи, т.е. является статически неопределимым. При кинематических расчетах учитывается один сателлит, так как остальные являются пассивными в кинематическом отношении.
. Их вводят с целью уменьшения габаритов механизма, снижения усилия в зацеплении, разгрузки подшипников центральных колес, улучшения уравновешивания водила, хотя механизм в этом случае имеет избыточные связи, т.е. является статически неопределимым. При кинематических расчетах учитывается один сателлит, так как остальные являются пассивными в кинематическом отношении. .
.
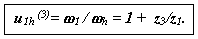 3....10
3....10

 7....16
7....16

 25....30
25....30


 , окончательно передаточное отношение планетарного редуктора может быть определено по формуле Виллиса:
, окончательно передаточное отношение планетарного редуктора может быть определено по формуле Виллиса: 



