
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Конические зубчатые передачи.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Они передают вращающий момент между валами с пересекающимися осями (чаще всего под углом 900). Их зубья бывают прямыми, косыми, круговыми и обычно имеют эвольвентный профиль.
Рис. 12. Конические зубчатые передачи В эквивалентных цилиндрических колёсах диаметр начальной окружности и модуль соответствуют среднему сечению конического зуба, вместо межосевого расстояния берётся среднее конусное расстояние, а профили эквивалентных зубьев получают развёрткой дополнительного конуса на плоскость. Конические зубчатые передачи применяют при пересекающихся (см. рис. 3.2, д, е, ж) или скрещивающихся осях (см. рис.3.2, з — гипоидная передача). Межосевой угол Конические зубчатые передачи по сравнению с цилиндрическими имеют большую массу и габариты, сложнее в изготовлении, а также монтаже, так как требуют точной фиксации осевого положения зубчатых колес. Наибольшее распространение имеют конические передачи с прямыми и криволинейными зубьями; последние постепенно вытесняют передачи с тангенциальными зубьями (см. рис.3.2, д, е, ж).'Конические зубчатые колеса с криволинейными зубьями могут иметь круговую, эвольвентную и циклоидальную линию зубьев; наиболее распространенные колеса с круговыми зубьями. Конические передачи с криволинейными зубьями по сравнению с прямозубыми имеют большую нагрузочную способность, работают более плавно и, следовательно, динамические нагрузки и шум при их работе меньше. Допуски для конических и гипоидных передач регламентированы стандартом, согласно которому установлено двенадцать степеней точности и соответствующие нормы точности. Предельные окружные скорости для конических прямозубых (непрямозубых) колес имеют следующие величины: при 6-й степени точности — до 12 (20) м/с, 7-й степени — до 8 (10) м/с, 8-й степени — до 4 (7) м/с, 9-й — до 1,5 (3) м/с. Расчет геометрии конических прямозубых передач регламентирован ГОСТом. На рис. 3.22 показаны основные геометрические параметры прямозубого цилиндрического колеса: Re, R — внешнее и среднее конусное расстояния; b — ширина зубчатого венца; d, de — средний и внешний
делительный диаметры; dae, d fe — внешние диаметры вершин зубьев и впадин; тельной головки и ножки зуба; Углы головки и ножки зуба сделаны одинаковыми для того, чтобы образующая конуса вершин зубьев одного колеса была параллельна образующей конуса впадины второго колеса, в результате чего радиальный зазор по длине прямого зуба будет постоянным (поэтому на рис. 3.22 вершины конусов не совпадают). По приведенным выше параметрам определяют остальные размеры колес и передачи, в частности: угол конуса вершин зубьев
угол конуса впадин
межосевой угол передачи (рис. 3.23)
У конических колес высота, толщина зубьев и окружной шаг по длине зуба неодинаковы, поэтому различают два окружных модуля: m — средний делительный окружной модуль, причем d = mz, где z — число зубьев колеса;
Внешний и средний модули пропорциональны соответствующим конусным расстояниям, поэтому
Для удобства измерений на чертежах задают внешние размеры зубьев и колес, а модуль те называют производственным, который обычно (но не обязательно) слндует округлить до стандартного значения. Рис.3.23 Существуют нормальные внешний и средний модули тne и тп. Профилирование зубьев конических колес с прямыми и тангенци- Внешний диаметр вершин зубьев равен dae = de + 2hm cosδ = me(z + 2cosδ). (3.40) Очевидно, что при Σ = 90°
а также Re = d/(2smδ), R=Re-b/2. (3.42) Углы делительных конусов ортогональных передач легко определяются в зависимости от числа зубьев ведущего и ведомого колес, а следовательно, от передаточного числа передачи: tgδ1 = d1/d2 = z1/z2 = 1/и или и = ctgδ1, = tgδ2. (3.43) Ширину зубчатого венца b по стандарту рекомендуется принимать
вычисленное значение округляется до целого числа, а при проектировании стандартных редукторов значения b принимаются по стандарту. Кроме ширины венца b указанный стандарт на ортогональные конические передачи для редукторов устанавливает номинальные значения внешнего делительного диаметра колеса de2 (в основном определяющего габариты редуктора) и номинальные значения передаточных чисел и (от и = 1 до и = 6,3, см. табл. 3.6). В приложении к ГОСТу имеется таблица, в которой для каждого стандартного значения передаточного числа и указаны взаимно согласованные значения de2 и b. Для прямозубых конических передач рекомендуется и < 3, для передач с криволинейными зубьями и < 6,3; число зубьев меньшего колеса рекомендуется z1 = 18...30. Эквивалентные колеса. Зубья конических колес профилируют по эвольвенте так же, как и зубья цилиндрических, но коническая передача является пространственной и поэтому точки ее сопряженных профилей лежат на сферической поверхности, которая не развертывается на плоскость. Поэтому профилирование зубьев конических колес с незначительной погрешностью выполняется на поверхности дополнительных конусов (см. Рис. 3.23) которые, мысленно разрезав по образующей, можно развернуть на плоскости. Образующие дополнительных конусов перпендикулярны образующим делительных конусов, поэтому диаметры воображаемых прямозубых цилиндрических колес, называемые эквивалентными колесами, определяются по формулам
где d1 и d2 — углы делительных конусов конических колес. Числа зубьев эквивалентных колес, называемые эквивалентными числами зубьев, равны
где z\ и z2 — действительные числа зубьев конических колес. Эквивалентным числом зубьев пользуются при определении коэффициента формы зуба по табл. 3.8 Силы в конической передаче. При силовом расчете конических передач полагают, что равнодействующая сил нормального давления Fn приложена в среднем сечении зуба, а силами трения, как и ранее, пренебрегают. Разложим силу Fn на три взаимно перпендикулярные составляющие по реальным направлениям (рис. 3.24), в результате чего получим: окружная сила на шестерне и колесе
радиальная сила на шестерне, численно равная осевой силе на колесе,
Расчет зубьев конической
так как при Подставив в ранее выведенную формулу для проверочного расчета цилиндрических колес параметры эквивалентного колеса (uv = и2, dvl = d1/cosδ1 = а также введя коэффициент понижения нагрузочной способности, равный 0,85, получим формулу для проверочного расчета зубьев конических прямозубых передач на контактную усталость:
где Z = 462-103 Па1/2 для стальных колес. Формула для проектного расчета прямозубых конических передач на контактную прочность выглядит следующим образом:
где для предварительных расчетов стальных колес Kd=7700 Па1/3,
Поскольку основным размером, определяющим габариты конической передачи, является внешний диаметр колеса, то формулу для проектного расчета прямозубых передач можно преобразовать и использовать в следующем виде:
Здесь de2 — внешний делительный диаметр колеса (de2 Расчет зубьев конической передачи на усталость при изгибе. Основным видом проектного расчета закрытых конических передач с низкой и средней твердостью зубьев является расчет на контактную усталость активных поверхностей зубьев, а расчет на усталость зубьев при изгибе применяется как проверочный. Исключением являются передачи с высокой твердостью активных поверхностей зубьев (Н > 50 HRC3, их нагрузочная способность лимитируется изгибной прочностью); параметры таких передач определяют из расчета зубьев на изгиб, причем основным расчетным параметром является модуль. Проектным расчетом открытых передач также является расчет на усталость зубьев при изгибе. Формула проверочного расчета на изгиб прямозубых конических передач имеет вид
где YF — коэффициент формы зуба, определяемый по табл. 3.8 по эквивалентному числу зубьев zv; параметр wFt = 2T1KFβKFv/(d1b); m — средний модуль. Формула проектного расчета на изгиб прямозубых конических передач имеет вид
где Кm = 1,4; коэффициент неравномерности нагрузки КFβ определяется по графику на рис. 3.19; числом зубьев шестерни задаются, обычно z, = 18...30; ум «0,166v и2 +1 (расчет ведется по шестерне).
По найденной величине среднего модуля определяется производственный модуль me, который можно округляют до стандартного значения по табл.3.1. Допускаемые напряжения для расчетов конических передач определяются так же) как для цилиндрических. Конические передачи с тангенциальными и криволинейными зубьями приближенно рассчитывают по тем же формулам, что и прямозубые, но по нормальному среднему модулю и с введением в знаменатель подкоренного выражения коэффициента Кk, учитывающего большую прочность этих зубьев. На основании опытных данных КHk = 1,5 — при расчетах зубьев на контактную усталость; KFk = 1,0 — при расчетах зубьев на изгиб. Коэффициент Кk вводится вместо коэффициента 0,85. Для обеспечения примерной равнопрочности зубьев на контактную усталость и изгиб внешний окружной модуль можно ориентировочно определять по формуле
(для прямозубых передач КFk = 0,85). Коэффициент формы зуба для криволинейных зубьев определяется по табл. 3.8 по биэквивалентному числу зубьев zv = z/(cosδ-cos3β), полученному двойным приведением: конического колеса к цилиндрическому и криволинейного зуба к прямому. Винтовые зубчатые передачи. Винтовая передача (разновидность косозубой) состоит из двух косозубых цилиндрических колес (рис. 41). Однако в отличие от косозубых цилиндрических передач с параллельными валами касания между зубьями здесь происходит в точке и при значительных скоростях скольжения. Поэтому при значительных нагрузках винтовые зубчатые передачи работать удовлетворительно не могут.
Рис.41. Винтовая зубчатая передача Червячные передачи.
Червячная передача - механизм, служащий для преобразования вращательного движения между скрещивающимися валами. Обычно червячная передача состоит из червяка 1 и червячного колеса 2 (рис. 3.14). Червячные передачи относятся к передачам зацеплением, в которых движение осуществляется по принципу винтовой пары: винтом является червяк, а червячное колесо представляет собой узкую часть длинной гайки, изогнутой по окружности резьбой наружу. Червячные передачи широко применяются в металлорежущих станках, подъёмно-транспортном оборудовании, транспортных машинах, в приборостроении. Зубья колеса имеют вогнутую форму, что увеличивает длину контактных линий с червяком и улучшает качество работы передачи. Достоинства червячных передач: • малые передаточные отношения (большие коэффициенты редукции); • компактность при большом коэффициенте редукции; • плавность зацепления и бесшумность работы; • самоторможение (не требуются тормозные, стопорные устройства); • передача больших вращающих моментов. Недостатки червячных передач: • повышенный износ червяка, колеса и их нагрев из-за трения; • сравнительно низкий КПД из-за трения (h = 0,5...0,92); • необходимость применения для венцов червячных колёс дорогих антифрикционных материалов (например, бронзы); • ограниченность передаваемой мощности (не выше 50...60 кВт). Передаточное отношение червячной передачи
где k - число заходов червяка; z - число зубьев червячного колеса. Скольжение в зацеплении. При движении витки червяка скользят по зубьям колеса, как в винтовой паре. КПД червячной передачи определяют по формуле
КПД увеличивается с увеличением числа заходов червяка (увеличивается Основные критерии работоспособности и расчета. Червячные передачи рассчитывают по напряжениям изгиба и контактным напряжениям. Здесь чаще наблюдается износ и заедание. Для предупреждения заедания применяют специальные антифрикционные пары материалов: червяк — сталь, колесо — бронза или чугун. . Основной расчет ведут по контактным напряжениям. Расчет по напряжениям изгиба выполняется как проверочный. Расчет по контактным напряжениям. Уравнение
применяют и для расчета червячных передач. Для архимедовых червяков радиус кривизны витков червяка в Расчет по напряжениям изгиба. На изгибную прочность рассчитывают только зубья колеса, так как витки червяка по материалу прочнее зубьев колеса. Тепловой расчет, охлаждение и смазка. В червячных передачах происходят значительные потери передаваемой мощности на трение, Поэтому для червячных редукторов производят тепловой расчет. Количество теплоты, выделяющейся в передаче в секунду, или тепловая мощность
где P 1 – мощность на входном валу, Вт; η – КПД передачи
|
||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 958; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.12.233 (0.011 с.) |

 И хотя, конические колёса сложнее цилиндрических как по своей геометрии, так и в изготовлении, принципы силового взаимодействия, условия работы, а следовательно, и методика расчёта аналогичны цилиндрическим.
И хотя, конические колёса сложнее цилиндрических как по своей геометрии, так и в изготовлении, принципы силового взаимодействия, условия работы, а следовательно, и методика расчёта аналогичны цилиндрическим.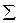 может изменяться в широком диапазоне значений (10° <
может изменяться в широком диапазоне значений (10° < 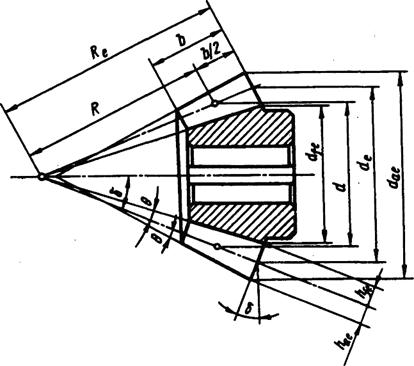 Рис. 3.22
Рис. 3.22 — угол делительного конуса; hас, h fe — внешняя высота дели-
— угол делительного конуса; hас, h fe — внешняя высота дели-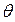 а =
а =  ; (3.37)
; (3.37) (3.38)
(3.38) (3.39)
(3.39) me — внешний делительный окружной модуль, причем de = mez.
me — внешний делительный окружной модуль, причем de = mez. .
. . (3.41)
. (3.41) или
или  ; (3.44)
; (3.44) (3.45)
(3.45) (3.46)
(3.46) (3.47)
(3.47)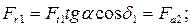 (3.48)
(3.48) осевая сила на шестерне, численно равная радиальной силе колеса
осевая сила на шестерне, численно равная радиальной силе колеса . (3.49)
. (3.49) ,
,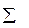 = 90° cosδ, = sinδ2, a tgδ2 = и.
= 90° cosδ, = sinδ2, a tgδ2 = и. ),
),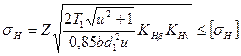 , (3.50)
, (3.50) (3.51)
(3.51)

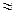 1,3, коэффициент ширины колеса относительно среднего диаметра шестерни
1,3, коэффициент ширины колеса относительно среднего диаметра шестерни  .
.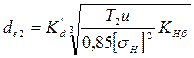 (3.52)
(3.52) l,17d2 =1,17d1u); K'd = 16 500 Па1/3 для стальных колес.
l,17d2 =1,17d1u); K'd = 16 500 Па1/3 для стальных колес. (3.53)
(3.53) , (3.54)
, (3.54) (3.55)
(3.55)



 ) и с уменьшением коэффициента трения или угла трения ф.
) и с уменьшением коэффициента трения или угла трения ф.




