
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особенности расчёта открытых цилиндрических зубчатых передачСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Расчёт открытой цилиндрической передачи производится на выносливость по напряжениям изгиба. При проектном расчёте предварительно выбирают Расчёт производят шестерни по формуле
где Коэффициенты Полученное значение модуля т округляют до ближайшего стандартного по ГОСТ 9563-60 (см.табл.1.13). Затем уточняют все остальные параметры передачи и производят проверочный расчёт по контактным напряжениям и по напряжениям изгиба.
2. РАСЧЕТ ЗАКРЫТОЙ КОНИЧЕСКОЙ ЗУБЧАТОЙ ПЕРЕДАЧИ 2.1. Проектный расчет
2.1.1. Внешний делительный диаметр колеса Определяется главный параметр - внешний делительный диаметр колеса
где Допускаемое контактное напряжение Полученное значение внешнего делительного диаметра колеса 2.1.2. Внешнее конусное расстояние и углы делительных конусов Внешнее конусное расстояние (
Значение Углы делительных конусов шестерни
Точность вычислений до четвёртого знака после запятой [2].
2.1.3.Ширина колёс и модуль Определяется ширина зубчатого венца шестерни и колес b, мм,
где Внешний окружной модуль
где Значение модуля, полученное с точностью до двух знаков после запятой, до стандартной величины не округлять. В силовых конических передачах следует принимать
2.1.4. Числа зубьев колёс
Числа зубьев колеса
Полученные значения После вычисления чисел зубьев уточняют фактическое передаточное число
И определяют его отклонение
При невыполнении нормы отклонения передаточного числа Определяют действительные углы делительных конусов шестерни
2.1.5. Выбор коэффициентов смещения Для конических передач с разностью средних твердостей шестерни и колеса выбрать из табл. 2.1 коэффициент смещения инструмента Таблица 2.1 Коэффициенты смещения
Для передач, у которых Z1 и u отличаются от указанных в табл. 2.1, коэффициентыxe1 и xn1принимают с округлением в большую сторону. Внешние диаметры шестерни и колеса вычисляют по формулам, приведённым ранее (см. часть 1, стр. 53). Точность вычисления делительных диаметров колес до 0,01 мм. Средние делительные диаметры шестерни
Значения d1 иd2 до целого числа не округлять. 2.2. Проверочный расчет 2.2.1. Проверочный расчет по контактным напряжениям Пригодность заготовок колес. Для конических шестерни и колеса вычисляют размеры заготовки, мм: + 6 мм;. Полученные расчётом значения и сравнивают с предельными размерами.Условие пригодности заготовок колес: После уточнения размеров передачи производят проверочный расчет по контактным напряжениям по формуле
где Если условие прочности не выполняется, то следует изменить ширину венца колеса и шестерни b. Если эта мера не даст должного результата, то либо надо увеличить внешний делительный диаметр колеса 2.2.2. Проверочный расчёт по напряжениям изгиба Напряжения изгиба зубьев шестерни
где
Для колес с круговыми зубьями
Допускаемые напряжения изгиба шестерни Если при проверочном расчете Таблица 2.2 Значения коэффициента формы зуба
3. РАСЧЕТ ЧЕРВЯЧНЫХ ПЕРЕДАЧ
3.1 Выбор электродвигателя Двигатель выбирают по методике, изложенной в п. 1.2, принимая ориентировочно КПД червячной передачи = 0,8. 3.2 Кинематический расчет Задачей кинематического расчета является определение передаточного числа червячной передачи, Его находят по формуле
где Полученную величину округляют до ближайшего стандартного значения. Допускаемое отклонение от стандартного передаточного числа - 4%. 3.3Проектировочный расчет 3.3.1. Определение допускаемых напряжений По рекомендациям [ 2 ] ориентировочно находят скорость скольжения Формулы для определения допускаемых контактных и изгибных напряжений приведены в табл. 3.1. Материалы группы Ш в редукторах общего назначения практически не используются, поэтому допускаемые напряжения для них в таблицу не внесены.
Таблица 3.1 Допускаемые напряжения для червячного колеса [2]
В формулах: Таблица 3.2 Значения коэффициента износа материала [2]
3.3.2. Определение межосевого расстояния Межосевое расстояние определяют по формуле
где Полученное значение 2.1.3. Определение числа витков червяка и числа зубьев червячного колеса Число витков червяка
с округлением до целого. По условию отсутствия подрезания зубьев рекомендуется 3.3.4. Определение модуля зацепления и коэффициента диаметра червяка Определяют модуль зацепления, мм,
и принимают ближайшее стандартное значение из 1-го ряда: 2,5; 3,15; 4; 5; 6,3; 8; 10; 12,5; 16. Допускается также использование 2-го ряда: 3; 3,5; 6; 7; 12. Коэффициент диаметра определяют по рекомендации
Полученную величину округляют до стандартной из 1-го ряда: 6,3; 8; 10; 12,5; 16 или из 2-го ряда: 7,1; 9; 11,2; 14; 18. По ГОСТ 19672-74 допускается также применение значений q =7,5 и q =12. 3.3.5.Определение коэффициента смещения инструмента Коэффициент смещения нарезающего инструмента находят из выражения
По условиям неподрезания и незаострения зубьев колеса величина смещения должна лежать в пределах -1 < х < +1. Если при расчете это не выполняется, то следует варьировать значениями q и 3.3.6.Определение фактических значений передаточного числа и межосевого расстояния Определяют фактическое передаточное число редуктора
и его отклонение от заданного
3.3.7. Определение основных геометрических размеров передачи размеры червяка: -делительный диаметр d1 = qm; -начальный диаметр d1w= m(q + 2х); -диаметр вершин витков = d1+ 2т; -диаметр впадин витков df1= d1-2,4m -делительный угол подъема витков Y= arctg(z1 /q); -длина нарезаемой части червяка b1 = (10 + 5,5|х| z1 + )m + С, при х<,0 С = 0, при х > 0 С = 100m/ z2 Размеры червячного колеса: -делительный диаметр -диаметр вершин зубьев da2 = d2 +2/m(l + х); -наибольший диаметр колеса -диаметр впадин зубьев df2 = d2 +2m(l,2 – х) -ширина венца при -радиусы закруглений зубьев Ra =05 d1 +m; Rf= 0,5d1 + 1,2m; - условный угол обхвата червяка венцом колеса 2 Проверочный расчет 3.4.1. Уточнение коэффициента полезного действия передачи Величину КПД определяют по формуле
где
В том случае, если получается < 0,8, следует заново подсчитать требуемую мощность электродвигателя и при необходимости назначить двигатель более мощный. Таблица 3.3 Значения угла трения
3.4.2. Проверка зубьев колеса по контактным напряжениям Контактное напряжение в зацеплении сравнивают с допускаемым:
где. = Допускаемая недогрузка передачи составляет 15%, допускаемая перегрузка-5%. 3.4.3. Проверка зубьев колеса по напряжениям изгиба Напряжение изгиба в зубе колеса сравнивают с допускаемым
где
Коэффициент формы зуба червячного колеса
Как правило, получается, 3.4.4. Проверка редуктора на нагрев Цель проверки (теплового расчета) - определить температуру масла в редукторе, которая не должна превышать допускаемую Температуру масла в корпусе червячной передачи при непрерывной работе находят по формуле
где Таблица 3.5 Площадь теплоотдающей поверхности корпуса червячного редуктора
При невыполнении условия 4. ПРОЕКТНЫЙ РАСЧЕТ ВАЛОВ
4.1. Быстроходный вал
Как правило, быстроходный вал и шестерню выполняют за одно целое - в виде вала-шестерни. Предварительный расчет характерного диаметра производят на кручение по пониженным допускаемым напряжениям. Диаметр входного конца вала определяют по формуле
где По ГОСТ 12080-66 принимают ближайшее к вычисленному значению диаметра. Затем назначают конструктивно диаметры ступенек под подшипники
с округлением до ближайшего стандартного диаметра внутреннего кольца подшипника. Составляют расчётную схему вала (пример на рис. 4.1). Определяют диаметр буртика
и принимают ближайший по ряду Ra 40. Предварительно выбирают подшипники. Как правило, для валов цилиндрических передач используют радиальные шариковые однорядные подшипники по ГОСТ 8338-75, а для валов конических и червячных передач - радиально- упорные роликовые по ГОСТ 333-79. Размещают подшипники в расточке корпуса редуктора, углубив их на 3... 5 мм от внутренней поверхности стенки. Определяют усилия, действующие на вал: усилие от соединительной муфты
и нагрузки, возникающие в передаче. Находят необходимые расстояния для определения опорных реакций. Для вала, приведённого на рис. 4.1, это делается следующим образом. Предварительно принимают по рекомендации [6] = (1,5...2) с округлением по ряду Ra 40. Вычисляют расстояние между точкой приложения усилия от муфты и реакции смежной опоры подшипника
где - ширина внутреннего кольца подшипника, - по ГОСТ 12080-66. Определяют расстояние между серединами подшипников
где
Тихоходный вал Определяют диаметр выходного конца вала
гдеi - номер тихоходного вала в редукторе (i =2 для двухступенчатого иi =3 для трёхступенчатого редуктора). Принимаем по ГОСТ 12080-66 Конструктивно назначают диаметры шеек вала под подшипники
с округлением до ближайшего стандартного значения диаметра внутреннего кольца подшипника. Принимают диаметр вала под зубчатым колесом
с округлением по ряду Ra 40. Определяют усилия, действующие на вал: Усилие от муфты
Определяем необходимые расстояния для вычисления реакций опор на тихоходном валу. Для вала, приведённого на рис. 4.2, это делается следуюим образом:
li=(0,8…1)diп; (4.11) сi=(bw1-bw2)/2; (4.12) LТ=bw2+2ci+2Δ+biп; (4.13) LТ=lМi + li- ci -biп/2. (4.14)
Промежуточный вал Определяют диаметр вала под колесом быстроходной ступени
с последующим округлением по Ra 40. Диаметр внутреннего кольца подшипника предварительно выбирают на 2...5 мм меньше, чем dкол округлением до стандартного размера. Отличительной особенностью промежуточного вала является наличие буртика между колесом быстроходной ступени и шестерней тихоходной ступени (см. рис. 4.3). Его диаметр dбурт принимают обычно на 3...6 мм больше, чем dкол по ряду Ra 40. Ширина буртика может лежать в пределах 3...5 мм. Определение длин участков вала производят по аналогии с п.п. 4.1 и 4.2. Каких-либо дополнительных пояснений здесь не требуется.
Рис. 4.2 – Расчетная схема тихоходного вала
Рис.4.3 – Расчетная схема промежуточного вала
5. ПРОВЕРОЧНЫЙ РАСЧЕТ ВАЛОВ
5.1. Быстроходный вал Проверочный расчет валов на прочность выполняют на совместное действие деформаций изгиба и кручения. При этом цель расчета - определить коэффициент запаса усталостной прочности и сравнить с допускаемым значением, равным [s] = 1,5...2,5 [2]. Рассмотрим расчёт на примере вала-шестерни. Материал вала тот же, что и для шестерни, так как это единая деталь (см. п.4.1). Расчетная схема вала представляет собой балку на двух опорах с приложенными к ней сосредоточенными силами (см. рис.4.1), определёнными в п.4.1. Силы в зацеплении считают приложенными посередине ширины венца шестерни. Консольную силу от муфты в тех случаях, когда тип муфты не конкретизируется, следует считать приложенной к концу вала. Важно правильно принять направление сил. Следует помнить, что окружная сила на шестерне направлена против направления вращения шестерни, радиальная сила направлена к оси вала, направление осевой силы зависит от направления окружной силы и направления наклона зуба, а консольная сила направлена параллельно окружной и в противоположную сторону. Затем определяют опорные реакции и строят эпюры изгибающих и крутящих моментов так, как это рассматривается в курсе сопротивления материалов. Выбирают опасное сечение вала. Следует учитывать, что опасным являстся не то сечение, диаметр которого меньше, и не то, в котором действуют наибольшие моменты, а то, которое имеет минимальный коэффициент запаса прочности - S. Коэффициент S — комплексный показатель, учитывающий не только размеры сечения и действующие в нём нагрузки, но и свойства материала, термообработку, наличие концентраторов напряжений и пр. Поиск опасного сечения сам по себе представляет серьёзную задачу и может включать в себя расчёт нескольких «подозрительных» сечений. Поскольку курсовой проект имеет учебный характер, студентам разрешается проверять одно сечение при условии грамотного обоснования его выбора. В качестве опасного сечения принято сечение А-А, в котором действуют большой изгибающий момент и имеется концентратор напряжения в виде посадки подшипника с натягом. Вычисляют нормальное амплитудное напряжение изгиба в опасном сечении вала
где МА - изгибающий момент в сечении А-А, Н·м; Wx - осевой момент сопротивления сечения вала, мм³ (для круглого сечения Wх = 0,1·diп3). Вычисляют амплитудное касательное напряжение в опасном сечении вала
где T1 - крутящий момент, Н·м; Wp - полярный момент инерции сопротивления сечения вала, мм³ (для круглого сечения Wp = 0,2·diп3). Определяют коэффициент концентрации нормальных напряжений в расчетном сечении вала
где Кσ - коэффициент концентрации нормальных напряжений (табл. 5.1); Кd - коэффициент влияния абсолютных размеров поперечного сечения (см. табл. 5.2); KF - коэффициент влияния шероховатости поверхности (для шероховатости поверхности по ряду Ra 2,5...0,63 мкм и σb =700 МПа KF = 1,1, при σb =900 МПа KF =1,15); Ky - коэффициент влияния поверхностного упрочнения (для валов без поверхностного упрочнения Ky =1). Определяют предел выносливости в расчетном сечении вала
где σ-1 - предел выносливости гладких образцов при симметричном цикле на-гружения, МПа;
Аналогично находят коэффициент концентрации касательных напряжений
где Кτ - коэффициент концентрации касательных напряжений (табл. 5.1). Затем определяют (τ-1) D – предел выносливости в расчетном сечении при кручении
где τ-1=0,58·σ-1- предел выносливости гладких образцов при кручении, МПа. Определяют коэффициенты
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 714; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.170.253 (0.012 с.) |

 - коэффициент ширины колеса по табл. 1.9. С целью уменьшения шума в быстроходных передачах число зубьев шестерни
- коэффициент ширины колеса по табл. 1.9. С целью уменьшения шума в быстроходных передачах число зубьев шестерни 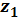 рекомендуется принимать больше 25, а для тихоходных передач можно принимать меньше.
рекомендуется принимать больше 25, а для тихоходных передач можно принимать меньше. (1.40)
(1.40) - вспомогательный коэффициент, для прямозубых передач
- вспомогательный коэффициент, для прямозубых передач  и
и  выбираются так же как и для закрытых передач по табл. 1.10 и табл. 1.17.
выбираются так же как и для закрытых передач по табл. 1.10 и табл. 1.17. мм [5]:
мм [5]: (2.1)
(2.1) - крутящий момент на колесе, Нм;
- крутящий момент на колесе, Нм;  - коэффициент, учитывающий распределение нагрузки по ширине венца (для прирабатывающихся колес с прямыми зубьями
- коэффициент, учитывающий распределение нагрузки по ширине венца (для прирабатывающихся колес с прямыми зубьями  = 1, с круговыми зубьями
= 1, с круговыми зубьями  - коэффициент вида конических колес (для прямозубых колес
- коэффициент вида конических колес (для прямозубых колес  ).
). определяется так же, как и для цилиндрических передач.
определяется так же, как и для цилиндрических передач. для нестандартных передач округлить до ближайшего значения из ряда нормальных линейных размеров (приложение 1).
для нестандартных передач округлить до ближайшего значения из ряда нормальных линейных размеров (приложение 1).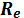 ) определяется по формуле
) определяется по формуле (2.2)
(2.2) до целого числа не округлять.
до целого числа не округлять. и колеса
и колеса  вычисляются по формулам
вычисляются по формулам (2.3)
(2.3)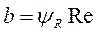 (2.4)
(2.4) = 0,285 - коэффициент ширины венца. Значение b необходимо округлять до целого числа по ряду Ra 40 (см. приложение 1).
= 0,285 - коэффициент ширины венца. Значение b необходимо округлять до целого числа по ряду Ra 40 (см. приложение 1). для прямозубых колес,
для прямозубых колес, 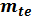 - для колес с круговыми зубьями вычисляют по формуле
- для колес с круговыми зубьями вычисляют по формуле (2.5)
(2.5) - коэффициент, учитывающий распределение нагрузки по ширине венца (для прирабатывающихся колес с прямыми зубьями
- коэффициент, учитывающий распределение нагрузки по ширине венца (для прирабатывающихся колес с прямыми зубьями  - коэффициент вида конических колёс (для прямозубых колес
- коэффициент вида конических колёс (для прямозубых колес  >1,5 мм, при этом в открытых передачах значение модуля
>1,5 мм, при этом в открытых передачах значение модуля 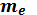 увеличить на 30% из-за повышенного изнашивания зубьев.
увеличить на 30% из-за повышенного изнашивания зубьев. определяют по формулам
определяют по формулам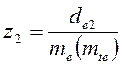 (2.6)
(2.6)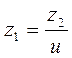 (2.7)
(2.7)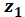 >15 - для колес с круговыми зубьями,
>15 - для колес с круговыми зубьями, 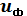
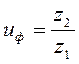 (2.8)
(2.8) от заданного
от заданного (2.9)
(2.9) и колеса
и колеса 
 (2.10)
(2.10)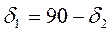 (2.11)
(2.11) для прямозубой шестерни и
для прямозубой шестерни и  для шестерни с круговым зубом. Коэффициенты смещения колес соответственно
для шестерни с круговым зубом. Коэффициенты смещения колес соответственно 
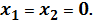

 при передаточном числе u
при передаточном числе u
 и колеса
и колеса  определяют по формулам:
определяют по формулам: (2.12)
(2.12) (2.13)
(2.13)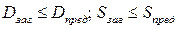 . При невыполнении неравенств изменить материал колес или вид термической обработки.
. При невыполнении неравенств изменить материал колес или вид термической обработки. (2.14)
(2.14) =2
=2 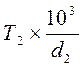 - окружная сила в зацеплении, Н; - коэффициент, учитывающий распределение нагрузки между зубьями колес (принимают
- окружная сила в зацеплении, Н; - коэффициент, учитывающий распределение нагрузки между зубьями колес (принимают  =1); - коэффициент динамической нагрузки (определяют в зависимости от окружной скорости колес
=1); - коэффициент динамической нагрузки (определяют в зависимости от окружной скорости колес  , м/с, и степени точности передачи, см. табл. 1.10);
, м/с, и степени точности передачи, см. табл. 1.10);  - угловая скорость вала колеса редуктора или открытой передачи, 1/с.
- угловая скорость вала колеса редуктора или открытой передачи, 1/с. и колеса
и колеса  , МПа:
, МПа: (2.15)
(2.15) (2.16)
(2.16) - коэффициент, учитывающий распределение нагрузки между зубьями колес (принимают
- коэффициент, учитывающий распределение нагрузки между зубьями колес (принимают  , - коэффициент динамической нагрузки, определяется аналогично коэффициенту
, - коэффициент динамической нагрузки, определяется аналогично коэффициенту  (см. табл. 1.10);
(см. табл. 1.10);  и
и  - коэффициенты формы зуба шестерни и колеса, определяют по табл. 2.2 в зависимости от эквивалентного числа зубьев шестерни
- коэффициенты формы зуба шестерни и колеса, определяют по табл. 2.2 в зависимости от эквивалентного числа зубьев шестерни  и колеса
и колеса  по формулам: для прямозубых колес
по формулам: для прямозубых колес (2.17)
(2.17) (2.18)
(2.18) (2.19)
(2.19) (2.20)
(2.20) = 35° - угол наклона зубьев;
= 35° - угол наклона зубьев;  - коэффициент, учитывающий наклон зуба (
- коэффициент, учитывающий наклон зуба (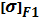 и колеса
и колеса  и определяются так же, как для цилиндрических передач.
и определяются так же, как для цилиндрических передач. значительно меньше
значительно меньше 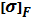 , то это допустимо, так как нагрузочная способность большинства зубчатых передач ограничивается контактной прочностью. Если
, то это допустимо, так как нагрузочная способность большинства зубчатых передач ограничивается контактной прочностью. Если  при коэффициенте смещения x.
при коэффициенте смещения x.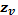
 (3.1)
(3.1) - частота вращения и угловая скорость червяка;
- частота вращения и угловая скорость червяка; 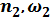 частота вращения и угловая скорость червячного колеса.
частота вращения и угловая скорость червячного колеса. и выбирают материал обода червячного колеса.
и выбирают материал обода червячного колеса. Н/мм^2
Н/мм^2
 Н/мм^2
Н/мм^2
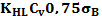
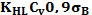



 - коэффициент долговечности при расчете по контактным напряжениям (
- коэффициент долговечности при расчете по контактным напряжениям ( 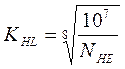 , где
, где 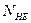 - эквивалентное число циклов нагружения, при
- эквивалентное число циклов нагружения, при  - коэффициент долговечности при расчете по напряжениям изгиба (
- коэффициент долговечности при расчете по напряжениям изгиба (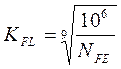 где
где  – эквивалентное число циклов нагружения, при
– эквивалентное число циклов нагружения, при  принимают
принимают  – коэффициент износа материала (табл.3.2).
– коэффициент износа материала (табл.3.2).
 (3.2)
(3.2) для редукторов общего назначения округляют до ближайшего по ряду нормальных размеров Ra 20.
для редукторов общего назначения округляют до ближайшего по ряду нормальных размеров Ra 20. = 4; при 14 < и < 30
= 4; при 14 < и < 30  (3.3)
(3.3)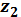 > 26.
> 26.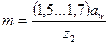 (3.4)
(3.4) (3.5)
(3.5)
 (3.6)
(3.6) (3.7)
(3.7)

 ;
; = arcsin[
= arcsin[  /(
/( )].
)]. (3.8)
(3.8) - угол трения, его принимают по табл. 3.3 в зависимости от фактической скорости скольжения
- угол трения, его принимают по табл. 3.3 в зависимости от фактической скорости скольжения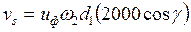 (3.9)
(3.9) м/с
м/с
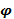
 30'...
...5°10'
30'...
...5°10'
 ...3°40'
...3°40'

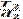 - окружная сила на колесе, Н; К - коэффициент нагрузки (принимается в зависимости от окружной скорости колеса
- окружная сила на колесе, Н; К - коэффициент нагрузки (принимается в зависимости от окружной скорости колеса  =
=  2000, м /с: при
2000, м /с: при  - уточненное значение допускаемого контактного напряжения по фактической скорости скольжения (см. табл. 3.1, 3.2).
- уточненное значение допускаемого контактного напряжения по фактической скорости скольжения (см. табл. 3.1, 3.2).


 так как нагрузочная способность червячных передач ограничивается не изгибной, а контактной выносливостью.
так как нагрузочная способность червячных передач ограничивается не изгибной, а контактной выносливостью. = 80...95°.
= 80...95°. (3.11)
(3.11)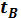 - температура окружающего воздуха, принимают
- температура окружающего воздуха, принимают  - мощность на червяке, Вт;
- мощность на червяке, Вт;  - коэффициент теплопередачи (среднее значение коэффициента Kt = 13 Вт/(м^2град)); А — площадь теплоотдающей поверхности корпуса (табл. 3.5), м2.
- коэффициент теплопередачи (среднее значение коэффициента Kt = 13 Вт/(м^2град)); А — площадь теплоотдающей поверхности корпуса (табл. 3.5), м2. следует увеличить площадь поверхности теплоотдачи с помощью оребрения. Если этой меры недостаточно, то необходимо предусмотреть специальные средства охлаждения (обдув корпуса вентилятором, введение в конструкцию холодильника для масла).
следует увеличить площадь поверхности теплоотдачи с помощью оребрения. Если этой меры недостаточно, то необходимо предусмотреть специальные средства охлаждения (обдув корпуса вентилятором, введение в конструкцию холодильника для масла). , (4.1)
, (4.1)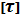 = 20 Мпа – допускаемое напряжение кручения.
= 20 Мпа – допускаемое напряжение кручения.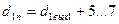 мм (4.2)
мм (4.2)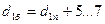 мм (4.3)
мм (4.3)
 (4.5)
(4.5) (4.6)
(4.6) - заглубление подшипника в корпус (см. выше); с - зазор между торцовой поверхностью шестерни и корпусом (рекомендуется с
- заглубление подшипника в корпус (см. выше); с - зазор между торцовой поверхностью шестерни и корпусом (рекомендуется с 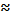 0,8
0,8  , где
, где 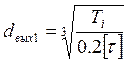 (4.7)
(4.7) и
и 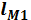
 (4.8)
(4.8) (4.9)
(4.9) (4.10)
(4.10)
 (4.15)
(4.15)

 (5.1)
(5.1) (5.2)
(5.2)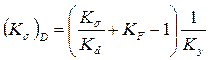 (5.3)
(5.3) (5.4)
(5.4) (5.5)
(5.5)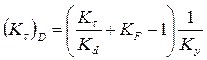 (5.6)
(5.6) (5.8)
(5.8)


