Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Различные модификации уравнений массоотдачи и массопередачиСодержание книги
Поиск на нашем сайте
МАССООБМЕН. Фазовые равновесия.
Основная задача химико-технологического процесса состоит в направленном изменении макроскопических свойств участвующих в процессе веществ: состава, агрегатного состояния, В изолированной системе условия равновесия записываются так:
p=const, T=const, Процесс переноса массы возникает самопроизвольно и протекает до тех пор, пока между фазами при данных условиях (Т и Условия (1.1) называют условиями механического, термического и химического равновесия. Все самопроизвольные процессы сопровождаются увеличением энтропии системы. В изолированной системе в состоянии равновесия энтропия достигает максимального значения:
Таким образом, для изолированной системы условия равновесия определяются условиями (1.1) и (1.2). Для открытой системы равновесное состояние может быть устойчивым лишь при её равновесии с окружающей средой. Движущая сила процессов переноса возникает вследствие отклонения от равновесия в самой системе или в окружающей среде. Химический потенциал зависит не только от концентрации данного компонента, но и от вида и концентрации других компонентов системы:
где Фазовые диаграммы:
Пример поглощения аммиака чистой водой из аммиачно-воздушной смеси: у - концентрация аммиака в воздухе, х - концентрация аммиака в воде. Аммиак - распределяемый компонент. С началом растворения аммиака в воде начнётся переход части его молекул в обратном направлении со скоростью, пропорциональной концентрации аммиака в воде. С течением времени скорость переноса аммиака в воду будет снижаться, а скорость обратного переноса возрастать.
Такой двусторонний перенос будет продолжаться до установления динамического равновесия – когда переходы в обоих направлениях будут равны. При равновесии достигается определённая зависимость между равновесными концентрациями распределяемого вещества в фазах при Т и
где у* - равновесная концентрация аммиака в воздухе, при концентрации аммиака в воде х. Графическое изображение (1.4) и есть линия равновесия.
у* = mx (1.5),
где m – коэффициент распределения.
Для двухкомпонентной двухфазной системы коэффициент распределения будет зависеть от двух переменных m=f(T,x)=f( Следовательно, необходимо иметь набор экспериментальных данных по равновесию по всей области изменения двух параметров. При увеличении числа компонентов в системе ситуация ещё более усложняется. При отсутствии таких экспериментальных данных для определения коэффициента распределения можно использовать аналитические зависимости. Такие зависимости рассмотрены у А. Разинова и Когана. Необходимо установить связь концентраций химическими потенциалами, а для
Материальный баланс. В стационарных условиях закон сохранения массы для всего аппарата в виде материального баланса может быть представлен:
Материальный баланс по распределённому компоненту при отсутствии хим. реакций
В случае постоянства расходов G и L уравнение (1.7) упрощается:
Для элементарного участка аппарата: - Знак минус свидетельствует о противоположном изменении концентрации распределяемого компонента в фазах, если в водной фазе увеличивается, то в другой – наоборот.
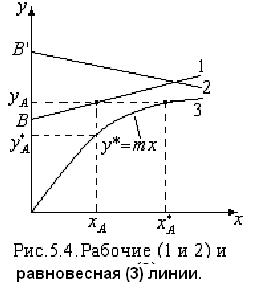
1.3 Уравнения рабочих и равновесных линий.
Из уравнения материального баланса можно получить уравнение рабочей линии. Уравнение материального баланса для нижней части аппарата до сечения А-А:
поступает расходуется Находим из (1.10) у: В случае постоянства расходов
Полученное уравнение (5.11) представляет собой уравнение прямой линии. Аналогичным образом может быть получено уравнение рабочей линии для прямоточного аппарата.
поступает расходуется
Находим у:
Запишем уравнение равновесной линии, связывающее рабочую концентрацию распределяемого компонента в одной из фаз с его равновесной концентрацией в другой фазе. Под равновесной концентрацией в произвольном сечении аппарата понимают концентрацию компонента в фазе, находящейся в равновесии с другой, состав которой определяется рабочей концентрацией. Уравнение равновесной линии: у*=mх (1.14)
Здесь у* - равновесная концентрация в фазе I, х – рабочая концентрация в фазе II, m – коэффициент распределения.
Рабочая концентрация в фазе I превышает равновесную. Поэтому распределяемый компонент будет переходить из I фазы во вторую, до равновесия т.к.
Ландау – Левича
Модель применима для больших значений диффузионного критерия Прандтля
Предполагается, что в ядре потока концентрация вещества постоянна, в пределах
Для систем жидкость – твёрдое тело m=3, для систем Г-Ж, Ж-Ж m=2. Модель обновления (Хигби) Модель обновления поверхности фазового контакта часто называют моделью проницания. По модели предполагается, что турбулентные пульсации постоянно подводят к поверхности раздела фаз свежую жидкость и смывают порции жидкости, уже прореагировавшей с газом (паром), т.е. каждый элемент поверхности жидкости взаимодействует с газом (паром) в течение некоторого времени t, после чего данный элемент обновляется. Предполагается, что t=const для всех элементов поверхности. Формула Хигби: Кишиневский, как и Хигби принимает время контакта t=const, но учитывает ещё турбулентные пульсации. Тогда в формуле (1.55) вместо D надо принимать (D+Dт). Недостаток модели: неизвестно как определить t.
Далее
Проблема состоит в определении При плёночном течении жидкости по стенкам цилиндрического аппарата и контакте её с газовым потоком имеем:
Для насадочного аппарата величину а можно выразить через удельную поверхность насадки
Величина
Таким образом, проектный расчёт аппарата с непрерывным контактом фаз в первом приближении завершён, D и Н найдены. Остаётся вопрос, оптимальны ли размеры аппарата? Критерием оптимальности могут служить затраты на проведение процесса. При заданных характеристиках первой фазы (
В качестве первого параметра оптимизации берём расход второй фазы В качестве второго параметра оптимизации возьмём фиктивную скорость Варьирование значениями параметров оптимизации позволяет спроектировать аппарат, обеспечивающий минимальные затраты на проведение процесса.
1.7.2 Технологический расчет аппарата со ступенчатым контактом фаз.
Особенность – существенная дискретная неоднородность удельной поверхности контакта фаз по высоте аппарата. Кроме того, в большинстве случаев для них не приемлемо допущение о параллельном движении фаз в режиме идеального вытеснения, которое использовалось при выводе основного уравнения массопередачи.
на примере тарельчатой колонны с противоточным N движением газовой и жидкой фаз (рис.5.9). yN xN Расход жидкой фазы определяется по формуле (1.56). N-1 Исходя из материального баланса каждому значению L yN-1 xN-1 соответствует значение хн, на L имеются ограничения
y l +1 x l +1 уравнениям (1.57).
у l -1 x l -1 у2 х2 Рис. 5.9. Изменение концентраций фаз по высоте 1 тарельчатой колонны. y1 x1
Высоту колонны можно связать с числом тарелок N и межтарельчатым расстоянием hм:
Величина Основная задача – определение N, обеспечивающих необходимый перенос распределяемого компонента из одной фазы в другую. Для этого вводится понятие эффективности тарелки по Мэрфри (КПД тарелки)
где Если
Следует отметить, что при этом составы фаз рассматриваются в различных сечениях аппарата (
Потарелочный расчёт колонны. Это аналитический метод определения N основан на решение уравнений материального баланса, равновесия и использования эффективности по Мэрфи для каждой тарелки. Для нижней тарелки под номером 1составы фаз известны Уравнение равновесия Уравнение Мэрфри Уравнение рабочей линии Находим составы фаз для тарелки 2. Далее, также для 3 тарелки и т.д. …
… Расчёт заканчивается при значении l, для которого начинает выполняться условие Для ориентировочных расчётов, выполняемых вручную, используют упрощенные графические способы нахождения числа тарелок.
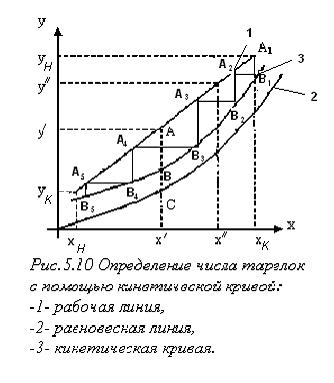
Определение числа тарелок с помощью кинетической кривой.
Эффективность по Мэрфри рассчитывается не для каждой тарелки, а лишь для нескольких сечений колонны, аналитическое решение уравнений (1.64-1.69) заменяется графическим. Алгоритм следующий: — строятся рабочая и равновесная линии; — для нескольких сечений аппарата (нескольких рабочих концентраций — эти отрезки делят в отношении, равному коэффициенту Мерфри Например — на диаграмме х – у наносятся точки — из точки
Определение числа тарелок с помощью КПД колонны
КПД колонны:
где
АБСОРБЦИЯ.
Абсорбцией называется процесс поглощения газов или паров из газовых или парогазовых смесей жидким поглотителем – абсорбентом. Если поглощаемый газ – абсорбтив – химически не взаимодействует с абсорбентом, то такая абсорбция физическая, если же абсорбтив образует с абсорбентом химическое соединение, то такой процесс называется хемосорбцией. Физическая абсорбция обратима, выделение поглощаемого газа из раствора – десорбция. Сочетание абсорбции и десорбции позволяют многократно использовать поглотитель и выделять поглощённый газ в чистом виде. Абсорбция применяется: — для получения готового продукта (абсорбция — для выделения ценных компонентов из газовых смесей (абсорбция бензола из коксового газа, абсорбция ацетилена из газов крекинга или пиролиза природного газа и т.д.), при этом абсорбцию проводят в сочетании с десорбцией;
— для очистки газовых выбросов от вредных примесей; — для осушки газов.
Прямоток.
Уходящий газ соприкасается с концентрированным раствором поглощаемого газа.
Тепловой баланс абсорбции
При изотермической абсорбции линия равновесия характеризуется кривой OАD. В случае неизотермической абсорбции, при растворении газа в жидкости температура её повышается вследствие выделения теплоты. Тогда линия равновесия характеризуется кривой ОАС. Для технических расчётов нагреванием газа пренебрегают, считают, что вся теплота идёт на нагрев жидкости. Если известна Т°К при данном составе, то можно найти по справочникам У* на кривой равновесия, соответствующую составу Х. Для этого нужно составить уравнение теплового баланса для части абсорбера, расположенной выше некоторого сечения с текущими концентрациями Х и У соответственно, т.е. в той части аппарата, где произошло поглощение газа:
Здесь
С помощью (2.13), задаваясь значениями Х в пределах Кинетика абсорбции. Физическая абсорбция. Применительно к абсорбции уравнение массопередачи, если движущую силу выражают в концентрациях газовой фазы, принимает вид:
Если движущую силу выразить в концентрациях жидкой фазы, то уравнение массопередачи имеет вид:
Коэффициенты массопередачи определяются:
В хорошо растворимых газах m незначительно, а Для процесса абсорбции в уравнение массопередачи (2.14) молярные концентрации газовой фазы может быть заменены парциальными давлениями газа, выраженными в долях общего давления:
Здесь Если равновесная линия прямая, то для
Здесь Если парциальное давление выражено в долях общего давления р, то коэффициенты массопередачи Хемосорбция. Если химическая реакция идет в жидкой фазе, то часть газообразного компонента переходит в связанное состояние. При этом концентрация свободного компонента в жидкости снижается и увеличивается движущая сила процесса. В общем случае скорость хемосорбции зависит как от скорости химической реакции, так и от скорости массопередачи между фазами. В зависимости от того, какая скорость определяет общую скорость переноса массы, различают кинетическую и диффузионную области процессов хемосорбции. В кинетической области скорость собственно химического взаимодействия меньше скорости массопереноса и поэтому лимитирует скорость всего процесса. В диффузионной области лимитирующей стадией является скорость диффузии компонентов в зоне реакции, которая зависит от гидродинамических условий в системе и определяется по основному уравнению массопередачи. Если скорости химической реакции и массопередачи соизмеримы, то такие процессы абсорбции протекают в смешанной, или диффузионно-кинетической области. Коэффициент массоотдачи в жидкой фазе
где Ф – фактор ускорения массообмена,
Конструкции абсорберов.
Абсорбция протекает на поверхности раздела фаз. По способу образования поверхности раздела фаз абсорберов можно разделить на 4 группы: - плёночные - насадочные - тарельчатые - распыливающие.
Плёночные абсорберы.
Вместо труб могут быть плоские листы. Пакет листовой насадки из различного материала. Допускаемая скорость воздуха W=3-6 м/с. Далее начинается захлёбывание (подвисание плёнки) аппарата. Δр аппарата – небольшие.
W газа > 10 м/с, Δр растёт, большие. Растёт Ку.
Насадочные абсорберы.
Они наиболее широко распространены в промышленности. Газ оттесняет жидкость к периферии. Поэтому насадки используются секциями высотой до 4D. Насадки – твёрдые тела различной формы. Жидкость в насадочной колонне течёт по элементу насадки в виде тонкой плёнки. При перетекании жидкости с одного элемента на другой плёнка жидкости разрушается и далее образуется вновь. Часть жидкости проходит вниз в виде струек, капель и брызг. Основные характеристики насадок: 1) удельная поверхность а ( 2) свободный объём ε ( 3) свободное сечение S ( Обычно принимают S = ε.
1 – сухой аппарат 2 – орошаемый аппарат Плёночный режим (до А) – наблюдается при небольших плотностях орошения и малых w газа. А – точка подвисания жидкости.
Второй режим – режим подвисания (торможения), после точки А повышение wг приводит к подтормаживанию жидкости газовым потоком. Поэтому wж уменьшается и количество удерживаемой жидкости увеличивается. Спокойное течение плёнки жидкости нарушается, возникают вихри, брызги, поэтому F увеличивается и увеличивается интенсивность процесса массопередачи. Этот режим заканчивается в точке В. Третий режим – режим эмульгирования. Увеличение wг приводит к накоплению жидкости в аппарате. При этом наступает инверсия фаз – жидкость становится дисперсионной средой, газ – дисперсной фазой. Образуется газожидкостная дисперсная система, по внешнему виду похожая на пену. Режим эмульгирования соответствует максимальной эффективности насадочных колонн. При этом резко возрастает Четвертый режим – режим уноса (C→), жидкость уносится из аппарата газовым потоком. В технике этот режим не используется. Требуется равномерное распределение газа по сечению аппарата. Насадки должны иметь как можно больше а, кроме того, они должны: - хорошо смачиваться орошаемой жидкостью; - оказывать малое гидравлическое сопротивление; - больше e и S; - обладать большой механической прочностью, стойкостью к агрессивным средам; - иметь невысокую стоимость. Тарельчатые абсорберы. ТА – вертикальные цилиндрические колонны, внутри которых на определённом расстоянии друг от друга на высоте колонны размещаются горизонтальные перегородки – тарелки. Тарелки служат для развития поверхности контакта фаз, жидкость течёт сверху вниз, а газ проходит снизу вверх. Процесс массопереноса идёт ступенчато. По способу слива жидкости с тарелками абсорберы бывают: - со сливными устройствами - без сливных устройств (неорганизованный слив жидкости). ТА без сливных устройств. В тарелке без сливных устройств газ и жидкость проходят через одни и те же отверстия и щели. При этом жидкость проваливается на нижнюю тарелку.
Разнообразны конструкции провальных тарелок. Гидродинамические режимы провальных тарелок: при низких wг жидкость на тарелке не задерживается, т.к. мала сила трения на поверхности контакта фаз. При постах точки А происходит скачкообразное увеличение В ТА без сливных устройств большой брызгоунос. Виды тарелок: дырчатые, решёточные, волнистые, трубчатые.
Распыливающие абсорберы. Эти абсорберы подразделяют на следующие группы: 1) полые (форсуночные); 2) скоростные прямоточные; 3) механически распыливающие.
ПЕРЕГОНКА ЖИДКОСТЕЙ. Перегонка жидкостей представляет собой процесс, в котором разделяемая жидкая смесь нагревается до кипения, а образующийся пар отбирается и конденсируется. В результате получают жидкость – конденсат, состав которого отличается от состава начальной смеси. Повторяя много раз процесс испарения конденсата и конденсации, можно практически полностью разделить исходную смесь на чистые составные части (компоненты). Процесс перегонки основан на том, что жидкости составляющие смесь, обладают различным давлением пара при одной и той же температуре. Поэтому состав пара, следовательно, состав конденсата отличается от состава исходной смеси: легколетучего (или низкокипящего - НК) в нем больше, чем в исходной смеси. Очевидно, что в неиспарившейся жидкости концентрация труднолетучего (или высококипящего - ВК) компонента будет больше, чем в исходной смеси. Если исходная смесь состоит из летучего и нелетучего компонента, то их разделяют выпариванием. Посредством же перегонки разделяют смеси, все компоненты которого летучи. Компоненты смеси обладают различной летучестью при одной и той же температуре. Жидкость, полученная в результате конденсации паров наз - ся дистиллятом (ректификатом), оставшаяся часть – остатком. Простая перегонка – процесс однократного частичного испарения смеси и конденсации образовавшихся паров. ПП применяют для разделения смесей, летучести компонентов которой существенно различны. Обычно ПП используют для предварительного грубого разделения жидких смесей. Ректификация - наиболее полное разделение смесей жидкостей, целиком или полностью растворимых друг в друге. Процесс заключается в многократном взаимодействии паров с жидкостью – флегмой, полученной при частичной конденсации паров.
Рис. 5.27 Насадочная ректификационная колона: 1 – колонна, 2 – дефлегматор, 3 - кипятильник Рассмотрим насадочную ректификационную колонну (рис.5.27), в котором снизу движутся пары, а сверху навстречу парам подают жидкость, представляющую почти чистый НК. При взаимодействии поднимающихся паров со стекающей жидкостью происходит частичная конденсация пара и частичное испарение жидкости (флегмы) за счет теплоты конденсации. При этом из пара конденсируется в основном ВК, а из флегмы, в основном, НК. Т.о., стекающая флегма непрерывно обогащается ВК, а поднимающиеся пары – НК. В результате выходящий из колонны пар состоит почти целиком из НК. Пар конденсируют в специальном теплообменнике – конденсаторе (дефлегматор). Часть этого конденсата в виде флегмы идет на орошение колонны, другая часть – дистиллят или ректификат – отбирают как готовый продукт. Для образования восходящих потоков газов колонну снабжают кипятильником, в котором происходит испарение части кубового остатка Кубовый остаток состоит почти из чистого ВК.
3.1. Равновесие в системах жидкость – пар.
В общем случае жидкая смесь может состоять из нескольких компонентов. В простейшем случае из двух, например, из компонентов A и B. Согласно правилу фаз, число степеней свободы такой системы = 2 (два компонента и две фазы). Следовательно, из трех независимых параметров, полностью определяющих состояние системы – T°C, p и концентр. одной из фаз – можно произвольно выбрать любые два: при этом определяется значение третьего параметра, которое не м.б. произвольным. По степени растворимости жидкости делятся: 1. Взаиморастворимые в любых соотношениях 1.1.1. Идеальные растворы – подчиняются закону Рауля 1.1.2. Нормальные растворы – частично подчиняются закону Р
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 573; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.153.224 (0.015 с.) |

 и Т. При этом происходит перенос субстанций: массы, энергии, импульса. Предельное состояние системы – подвижное равновесие, при котором не происходит изменений макроскопических свойств веществ. Равновесным называют такое состояние системы, при котором перенос субстанций отсутствует.
и Т. При этом происходит перенос субстанций: массы, энергии, импульса. Предельное состояние системы – подвижное равновесие, при котором не происходит изменений макроскопических свойств веществ. Равновесным называют такое состояние системы, при котором перенос субстанций отсутствует. ,
,  ,
,  (1.1)
(1.1) =const – химический потенциал
=const – химический потенциал  -того компонента.
-того компонента. (1.2)
(1.2) (1.3),
(1.3),
 значение химического потенциала при стандартном состоянии (обычно при
значение химического потенциала при стандартном состоянии (обычно при 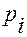 =0.1 МПа),
=0.1 МПа), 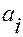 - активность
- активность  и
и 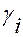 -соответственно, мольная доля и коэффициент активности
-соответственно, мольная доля и коэффициент активности 
 , (1.4)
, (1.4) условие равновесия имеет простой вид d
условие равновесия имеет простой вид d 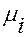 =0. Конкретный вид равновесия (1.5) различен для разных процессов массопередачи. Например, для абсорбции равновесие описывается законом Генри, для ректификации – законом Рауля и т.д. Зная линию равновесия для конкретного процесса и рабочую линию можно определить направление и движущую силу массопередачи в любой точке аппарата.
=0. Конкретный вид равновесия (1.5) различен для разных процессов массопередачи. Например, для абсорбции равновесие описывается законом Генри, для ректификации – законом Рауля и т.д. Зная линию равновесия для конкретного процесса и рабочую линию можно определить направление и движущую силу массопередачи в любой точке аппарата. (1.6)
(1.6)
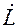 ,
, 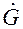 – соответственно, расходы жидкой и газовой фаз; х, у – конц. распределяемого комп. в фазах; н – начальное, к – конечное состояние; I и II – номера фаз.
– соответственно, расходы жидкой и газовой фаз; х, у – конц. распределяемого комп. в фазах; н – начальное, к – конечное состояние; I и II – номера фаз. (1.7)
(1.7) (1.8)
(1.8)
 (1.10)
(1.10)
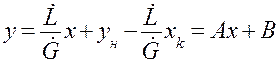 (1.11)
(1.11)
 (1.12)
(1.12) , если расходы не меняются, т.е.
, если расходы не меняются, т.е.  (1.13)
(1.13)
 .
. .
.
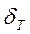 (турбулентный подслой) концентрация снижается, в вязком подслое
(турбулентный подслой) концентрация снижается, в вязком подслое  концентрация уменьшается очень быстро, в пределах диффузионного подслоя
концентрация уменьшается очень быстро, в пределах диффузионного подслоя  молекулярный перенос становится основным.
молекулярный перенос становится основным. (1.54)
(1.54)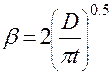 (1.55)
(1.55) (1.59)
(1.59) .
. (1.60)
(1.60)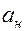 и долю активной поверхности
и долю активной поверхности  :
: (1.61)
(1.61) может быть и больше единицы за счёт образования волн на поверхности плёнки и брызг жидкости при высоких скоростях газового потока.
может быть и больше единицы за счёт образования волн на поверхности плёнки и брызг жидкости при высоких скоростях газового потока. . При увеличении
. При увеличении  и
и  , что приводит к уменьшению V, но растёт Δр аппарата.
, что приводит к уменьшению V, но растёт Δр аппарата.











 массообменного аппарата со ступенчатым контактом фаз
массообменного аппарата со ступенчатым контактом фаз



 l
l



 (1.62)
(1.62)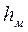 , являясь одним из параметров оптимизации, в первом приближении мажет определяться из условия максимально допустимого уноса капель газовым потоком. Для различных типов тарелок имеются соотношения связывающие величину уноса е с
, являясь одним из параметров оптимизации, в первом приближении мажет определяться из условия максимально допустимого уноса капель газовым потоком. Для различных типов тарелок имеются соотношения связывающие величину уноса е с  и скоростью газовой фазы
и скоростью газовой фазы  жидкости на 1 кг газа.
жидкости на 1 кг газа.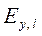 , характеризующее степень достижения равновесия между уходящими с тарелки фазами:
, характеризующее степень достижения равновесия между уходящими с тарелки фазами: (1.63)
(1.63) - концентрация распределяемого компонента в газовой фазе, равновесная с уходящим с l -ой тарелки потоком жидкости. Аналогичным образом можно найти
- концентрация распределяемого компонента в газовой фазе, равновесная с уходящим с l -ой тарелки потоком жидкости. Аналогичным образом можно найти  , используя концентрации жидкой фазы.
, используя концентрации жидкой фазы. , то такую тарелку называют теоретической. Т.е. имеем такой объём аппарата, концентрация распределяемого вещества на выходе из которого
, то такую тарелку называют теоретической. Т.е. имеем такой объём аппарата, концентрация распределяемого вещества на выходе из которого  равна равновесной концентрации на входе в него:
равна равновесной концентрации на входе в него:  . В этом объёме аппарата происходит процесс полного (теоретического) обмена распределяемого вещества между обеими фазами.
. В этом объёме аппарата происходит процесс полного (теоретического) обмена распределяемого вещества между обеими фазами. - над l -ой тарелкой,
- над l -ой тарелкой,  - под ней). Таким образом, в любом поперечном сечении аппарата равновесие не достигается
- под ней). Таким образом, в любом поперечном сечении аппарата равновесие не достигается  , иначе отсутствовала бы движущая сила массопередачи.
, иначе отсутствовала бы движущая сила массопередачи.
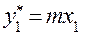 (1.64)
(1.64)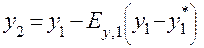 (1.65)
(1.65)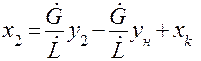 (1.66)
(1.66) (1.67)
(1.67) (1.68)
(1.68) (1.69)
(1.69) , при этом число тарелок N= l. Поскольку число тарелок в аппарате может достигать сотни и более, данный алгоритм необходимо реализовать на компьютере.
, при этом число тарелок N= l. Поскольку число тарелок в аппарате может достигать сотни и более, данный алгоритм необходимо реализовать на компьютере. ;
;  ;
;  ) определяют отрезки
) определяют отрезки 
 и находят величины.
и находят величины. 
 :
:  (1.70)
(1.70) и т.д. Соединяя их получим кинетическую кривую.
и т.д. Соединяя их получим кинетическую кривую. спускаемся по лестнице до тех пор, пока для точки В l не выполнится условие
спускаемся по лестнице до тех пор, пока для точки В l не выполнится условие  . На этом построение заканчивается, необходимое число тарелок в колонне
. На этом построение заканчивается, необходимое число тарелок в колонне  .
.
 (1.71)
(1.71) - теоретическое число тарелок, N – действительное число тарелок. Величина
- теоретическое число тарелок, N – действительное число тарелок. Величина  находится из опыта. Найти
находится из опыта. Найти  опытным путём достаточно сложно. Необходимы данные по идентичной колонне.
опытным путём достаточно сложно. Необходимы данные по идентичной колонне. в производстве серной кислоты, абсорбция HCl, оксидов азота водой в производстве азотной кислоты);
в производстве серной кислоты, абсорбция HCl, оксидов азота водой в производстве азотной кислоты);

 . Поэтому расхода абсорбента меньше, чем при противотоке.
. Поэтому расхода абсорбента меньше, чем при противотоке.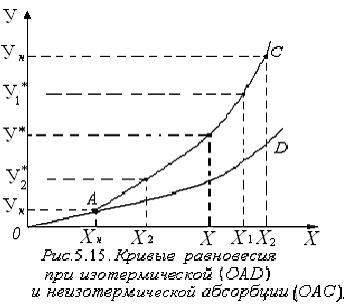
 (2.14)
(2.14) - дифференциальная теплота растворения газа, кДж/кмоль;
- дифференциальная теплота растворения газа, кДж/кмоль; 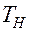 - начальная температура жидкости, К. Находим Т:
- начальная температура жидкости, К. Находим Т: (2.13)
(2.13) и
и 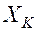 находим ряд Т и по справочникам далее находим ряд
находим ряд Т и по справочникам далее находим ряд 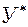 и строим по точкам ОАС.
и строим по точкам ОАС. (2.14)
(2.14) (2.15)
(2.15)
 велика, т.е. мало сопротивление в жидкой фазе, тогда
велика, т.е. мало сопротивление в жидкой фазе, тогда  и можно принять
и можно принять 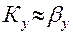 . Для плохо растворимых газов можно пренебречь диффузионным сопротивлением в газовой фазе, так как
. Для плохо растворимых газов можно пренебречь диффузионным сопротивлением в газовой фазе, так как  велики и можно принять
велики и можно принять  .
. (2.18)
(2.18) - средняя движущая сила процесса, выраженная в единицах давления;
- средняя движущая сила процесса, выраженная в единицах давления;  - коэффициент массопередачи, отнес. к единице движущей силы, выражаемой через парциальные давления поглощаемого газа.
- коэффициент массопередачи, отнес. к единице движущей силы, выражаемой через парциальные давления поглощаемого газа. (2.19)
(2.19) (2.20)
(2.20) - соответственно, парциальные давления газа на входе в аппарат и выходе из него;
- соответственно, парциальные давления газа на входе в аппарат и выходе из него;  - равновесные парциальные давления газа на входе в аппарат и на выходе из него.
- равновесные парциальные давления газа на входе в аппарат и на выходе из него. и
и  численно равны, если парциальные давления выражены в единицах давления, то
численно равны, если парциальные давления выражены в единицах давления, то  .
. при протекании химической реакции можно определить:
при протекании химической реакции можно определить: (2.21)
(2.21) .
.



 /
/  );
);
 аппарата (отрезок ВС). Поддерживать этот режим затруднительно. По скорости газа режим очень узок.
аппарата (отрезок ВС). Поддерживать этот режим затруднительно. По скорости газа режим очень узок.