
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Число и высота единиц переносаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Для наиболее распространённого типа массообменных аппаратов – цилиндрические вертикальные колонны – основным размером, зависящим от скорости массопередачи, является высота Н. Если S (площадь поперечного сечения аппарата) const, то его объём можно записать:
Находим
Получим
Для процесса массотдачи можно получить Н аналогичным образом:
По другой фазе:
В уравнениях (1.43) – (1.46) первые сомножители называются высотой единицы переноса (ВЕП), а вторые – числом единиц переноса (ЧЕП), причём Тогда по смыслу Общее ЧЕП можно представить по-разному.
Аналогичные соотношения могут быть получены и для частных ЧЕП:
Подобно тому, как коэффициенты массопередачи выражаются через коэффициенты массоотдачи, общее ЧЕП может быть выражено через частное ЧЕП:
Здесь
Для другой фазы: Высота единиц переноса (ВЕП) соответствует высоте участка аппарата, эквивалентного одной единице переноса. ВЕП обычно пропорциональны коэф. массоотдачи и массопередачи. Чем больше эти коэффициенты, тем меньше ВЕП и тем меньше высота аппарата, обеспечивающая требуемое разделение веществ.
Общие ВЕП могут быть выражены через частные:
ЧЕП и ВЕП обычно находят из уравнений, полученных обобщением экспериментальных данных.
Аналогия тепло - и массообмена Аналогия подразумевает возможность использования результатов, полученных для межфазного переноса одного вида субстанции, применительно к описанию переноса другого вида субстанции. Это возможно, когда дифференциальные уравнения и условия однозначности идентичны. Для двухкомпонентных смесей уравнения нестационарной конвективной диффузии и теплопроводности идентичны. Это позволяет использовать соотношения, характеризующие теплообмен, для описания массообмена при соблюдении гидродинамического подобия и идентичности краевых условий переноса тепла и массы. Для этого удобнее использовать критерии подобия Nu, Pr, У Разинова рассмотрены случаи: — массообмен в плоской полубесконечной пластине с неограниченным потоком (ламинарный и турбулентный режимы); — массообмен в трубе; — массообмен в твёрдой фазе.
Упрощенные модели массоотдачи Коэффициент массоотдачи характеризует скорость переноса вещества внутри фазы конвекцией и молекулярной диффузией одновременно. Коэффициент массоотдачи зависит от многих факторов: физических свойств фазы, скорости потока, определяющих геометрических радиусов и т.д. Определение β требует совместного решения уравнений движения, неразрывности и конвективной диффузии. Это можно сделать для простейшего случая, когда известна поверхность контакта фаз и режим ламинарный. Поэтому для определения β иногда пользуются упрощёнными моделями. Плёночная модель (Нернст, Льюис, Уитмен) Предполагается, что вблизи межфазной поверхности располагается тонкая неподвижная или ламинарно движущаяся плёнка толщиной
Параметром модели является
Модель турбулентного диффузионного пограничного слоя Ландау – Левича
Модель применима для больших значений диффузионного критерия Прандтля
Предполагается, что в ядре потока концентрация вещества постоянна, в пределах
Для систем жидкость – твёрдое тело m=3, для систем Г-Ж, Ж-Ж m=2. Модель обновления (Хигби) Модель обновления поверхности фазового контакта часто называют моделью проницания. По модели предполагается, что турбулентные пульсации постоянно подводят к поверхности раздела фаз свежую жидкость и смывают порции жидкости, уже прореагировавшей с газом (паром), т.е. каждый элемент поверхности жидкости взаимодействует с газом (паром) в течение некоторого времени t, после чего данный элемент обновляется. Предполагается, что t=const для всех элементов поверхности. Формула Хигби: Кишиневский, как и Хигби принимает время контакта t=const, но учитывает ещё турбулентные пульсации. Тогда в формуле (1.55) вместо D надо принимать (D+Dт). Недостаток модели: неизвестно как определить t.
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1275; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 (1.42)
(1.42)

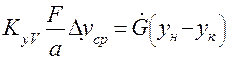 ,
, 
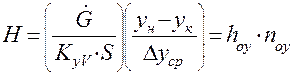 (1.43)
(1.43) (1.44)
(1.44) (1.45)
(1.45) (1.46)
(1.46)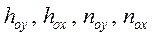 - называются общими, а
- называются общими, а  - частными или фазовыми.
- частными или фазовыми.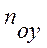 и
и  - общее ЧЕП – изменение рабочей концентрации распределяемого между фазами компонента, приходящееся на единицу движущей силы. Тогда одна единица переноса соответствует участку аппарата, для которого изменение рабочей концентрации фазы равно средней движущей силе на этом участке.
- общее ЧЕП – изменение рабочей концентрации распределяемого между фазами компонента, приходящееся на единицу движущей силы. Тогда одна единица переноса соответствует участку аппарата, для которого изменение рабочей концентрации фазы равно средней движущей силе на этом участке.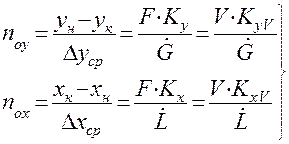 (1.47)
(1.47) (1.48)
(1.48)

 - фактор процесса массопередачи. Итак, получили:
- фактор процесса массопередачи. Итак, получили: (1.49)
(1.49)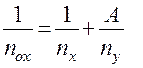 (1.50)
(1.50) (1.51)
(1.51) (1.52)
(1.52) , критерии теплового подобия меняем на диффузионные.
, критерии теплового подобия меняем на диффузионные.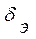 , в которой сосредоточено всё сопротивление массоотдачи. Таким образом, эта плёнка представляет собой диффузионный пограничный слой:
, в которой сосредоточено всё сопротивление массоотдачи. Таким образом, эта плёнка представляет собой диффузионный пограничный слой: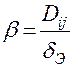 (1.53)
(1.53)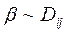 - (прямая пропорциональность), что не подтверждается на практике. Данная модель пригодна лишь для качественного анализа.
- (прямая пропорциональность), что не подтверждается на практике. Данная модель пригодна лишь для качественного анализа. .
.
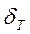 (турбулентный подслой) концентрация снижается, в вязком подслое
(турбулентный подслой) концентрация снижается, в вязком подслое  концентрация уменьшается очень быстро, в пределах диффузионного подслоя
концентрация уменьшается очень быстро, в пределах диффузионного подслоя  молекулярный перенос становится основным.
молекулярный перенос становится основным. (1.54)
(1.54)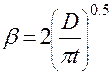 (1.55)
(1.55)


