
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Турбулентный перенос теплоты и кол-ва движения в пограничном слое
Турбулентный перенос теплоты и кол-ва движения в пограничном слое Отклонения мгновенной скорости потока w, от средней во времени называются пульсациями скорости или пульсационными скоростями. При этом скорость равна
Таким образом, турбулентное движение состоит из регулярного течения и наложенного на него хаотического пульсационного течения (см. рис. 12.4). Пульсации скорости приводят к переносу теплоты, вследствие чего возникают пульсации температур. Поэтому турбулентное течение не является стационарным. Зависимость среднего коэффициента теплоотдачи и локального коэффициента теплоотдачи от коэффициента трения аналогична как для турбулентного режима течения (соблюдается гидродинамическая аналогия теплообмена Рейнольдса).
Билет №2 1) Температурное поле Аналитически распределение температуры в теле описывается с помощью уравнения:
Это математическое описание температурного поля в теле. Если температура в данной точке не меняется по времени, т.е. Если температура меняется только вдоль одной из координат (пусть х), то такое температурное поле называется одномерным:
Для двухмерного нестационарного температурного поля:
Температурный градиент Геометрическое место точек, имеющих одинаковую температуру, называют изотермической поверхностью. Эти поверхности не пересекаются и заканчиваются либо внутри тела, либо на его поверхности. Скорость изменения температуры вдоль определённого направления характеризует градиент температуры. 2) Регулярный режим нагревания (охлаждения) тел Регулярный- режим нагрев/охлажд с постоянным темпом нагрев/охлажд Темп нагрев/охлажд- относительная скорость изменения темпер в теле
первую теорему Кондратьева: Темп охлаждения или относительная скорость изменения температуры в теле прямо пропорционален среднему коэффициенту теплоотдачи, поверхности тела F и обратно пропорционален теплоёмкости тела.
3) При свободном движении температура жидкости в пограничном слое изменяется от Режим движения классифицируется в зависимости от числа Релея
Интенсивность теплоотдачи при естественной конвекции характеризуется коэффициентом теплоотдачи, который определяется из формулы Ньютона:
Таким образом, коэффициент теплоотдачи характеризует количество тепла, отдаваемое в единицу времени единицей поверхности при разности температур между поверхностью и жидкостью в 1 градус.
Билет №3
Тепловой поток. Закон теплопроводности Фурье По гипотезе Фурье количество теплоты (в джоулях), проходящее через элементарную площадку dF за время dτ прямо пропорционально градиенту температуры Плотность теплового потока – количество теплоты, проходящее в единицу времени через единицу изотермической поверхности.
Тепловой поток – количество теплоты, проходящее в единицу времени.
Первая теорема Кондратьева Если обозначить через Темп охлаждения или относительная скорость изменения температуры в теле прямо пропорционален среднему коэффициенту теплоотдачи, поверхности тела F и обратно пропорционален теплоёмкости тела. Вторая теорема Кондратьева При Bi®¥ (a®¥) темп охлаждения m становится прямо пропорциональным коэффициенту температуропроводности a:
Билет №4 Теплообмен при ламинарном режиме течения жидкости в трубах При ламинарном режиме различают два режима течения жидкости: 1) вязкостный; 2) вязкостно-гравитационный. Вязкостный режим Для вязкостного режима силы вязкости являются преобладающими (отсутствует влияние естественной конвекции). Вязкостный режим более вероятен в трубах малого диаметра, когда течёт очень вязкая жидкость (например, мазут), и когда имеет место малый температурный напор между поверхностью жидкости и стенки. Билет №5 Билет №6 Конвективный теплообмен. Основные понятия Конвекция возможна только в текучей среде, в которой перенос теплоты связан с переносом самой среды. Конвективный теплообмен – это совместный перенос теплоты за счёт теплопроводности и конвекции. Конвекция – это перенос теплоты при перемещении жидкости или газа в пространстве с одной температурой в пространство с другой температурой. Если в единицу времени через единицу контрольной поверхности перпендикулярно к ней проходит масса жидкости, Основное уравнением конвективного теплообмена – это уравнение теплоотдачи Ньютона-Рихмана.
a – количество теплоты, воспринимаемое единицей поверхности в единицу времени при разности температур
Билет №7 Билет №8 Билет№9 1) Теплопередача через плоскую стенку (при граничных условиях III рода) Теплопередача – процесс теплообмена между двумя средами (теплоносителями), разделёнными стенкой (перегородкой). В этом случае при граничных условиях III-рода задаются температуры сред теплоносителей, коэффициенты теплоотдачи
Полное количество теплоты, передаваемое через стенку за время τ
Билет№10 Условиях I-рода.) 2) Уравнение движения (уравнение Навье-Стокса) Навье-Стокса) для движущейся жидкости в гравитационном поле имеет вид:
Уравнение Навье-Стокса подтверждает второй закон Ньютона: произведение массы на ускорение равно сумме сил. Т.е. уравнение баланса количества движения соответствует второму закону Ньютона. Для частного случая, когда силами вязкого трения можно пренебречь для идеальной жидкости, уравнение Навье-Стокса превращается в уравнение Эйлера
Из (11.14) для установившегося безвихревого движения в поле силы тяжести энергетический баланс для элементарной струи жидкости описывается уравнением Бернулли:
Билет №11 1) Теплопередача через цилиндрическую стенку (при граничных условиях III-рода) Тепловой поток для цилиндрической стенки рассчитывается:
Билет№12 Билет№13 Билет№14 Тепловое подобие Тепловое подобие – это подобие температурных полей и тепловых потоков. Билет№15 Билет№16 Билет№17 Числа теплового подобия Тепловое подобие – это подобие температурных полей и тепловых потоков
Билет№19 Основные положения Конвекция возможна только в текучей среде, в которой перенос теплоты связан с переносом самой среды. Конвективный теплообмен – это совместный перенос теплоты за счёт теплопроводности и конвекции. Конвекция – это перенос теплоты при перемещении жидкости или газа в пространстве с одной температурой в пространство с другой температурой. Основное уравнением конвективного теплообмена – это уравнение теплоотдачи Ньютона-Рихмана.
Билет №29 Турбулентный перенос теплоты и кол-ва движения в пограничном слое Отклонения мгновенной скорости потока w, от средней во времени называются пульсациями скорости или пульсационными скоростями. При этом скорость равна
Таким образом, турбулентное движение состоит из регулярного течения и наложенного на него хаотического пульсационного течения (см. рис. 12.4). Пульсации скорости приводят к переносу теплоты, вследствие чего возникают пульсации температур. Поэтому турбулентное течение не является стационарным. Зависимость среднего коэффициента теплоотдачи и локального коэффициента теплоотдачи от коэффициента трения аналогична как для турбулентного режима течения (соблюдается гидродинамическая аналогия теплообмена Рейнольдса).
Билет №2 1) Температурное поле Аналитически распределение температуры в теле описывается с помощью уравнения:
Это математическое описание температурного поля в теле. Если температура в данной точке не меняется по времени, т.е. Если температура меняется только вдоль одной из координат (пусть х), то такое температурное поле называется одномерным:
Для двухмерного нестационарного температурного поля:
Температурный градиент Геометрическое место точек, имеющих одинаковую температуру, называют изотермической поверхностью. Эти поверхности не пересекаются и заканчиваются либо внутри тела, либо на его поверхности. Скорость изменения температуры вдоль определённого направления характеризует градиент температуры. 2) Регулярный режим нагревания (охлаждения) тел Регулярный- режим нагрев/охлажд с постоянным темпом нагрев/охлажд Темп нагрев/охлажд- относительная скорость изменения темпер в теле
первую теорему Кондратьева: Темп охлаждения или относительная скорость изменения температуры в теле прямо пропорционален среднему коэффициенту теплоотдачи, поверхности тела F и обратно пропорционален теплоёмкости тела.
3) При свободном движении температура жидкости в пограничном слое изменяется от Режим движения классифицируется в зависимости от числа Релея
Интенсивность теплоотдачи при естественной конвекции характеризуется коэффициентом теплоотдачи, который определяется из формулы Ньютона:
Таким образом, коэффициент теплоотдачи характеризует количество тепла, отдаваемое в единицу времени единицей поверхности при разности температур между поверхностью и жидкостью в 1 градус.
Билет №3
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.166.141 (0.009 с.) |
 , где w¢ – пульсационная скорость
, где w¢ – пульсационная скорость (12.24)
(12.24)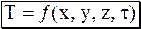 . (1.1)
. (1.1)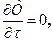 то такое температурное поле называется стационарным, если наоборот, если
то такое температурное поле называется стационарным, если наоборот, если  то такое температурное поле называется нестационарным.
то такое температурное поле называется нестационарным. ,
,  .
. ,
,  .
. (1)
(1) . (9.19)
. (9.19) , (вторая теорема Кондратьева) (9.20)
, (вторая теорема Кондратьева) (9.20) – до –
– до –  , а скорость от нуля у стенки до максимума. На большом удалении от стенки скорость снова равна нулю. Скорость движения среды определяют характер (режим) движения – плёночный, ламинарный или турбулентный. С изменением характера движения изменяется и теплоотдача.
, а скорость от нуля у стенки до максимума. На большом удалении от стенки скорость снова равна нулю. Скорость движения среды определяют характер (режим) движения – плёночный, ламинарный или турбулентный. С изменением характера движения изменяется и теплоотдача. (1)
(1) (2)
(2) . (1.5)
. (1.5) ,
,  , (1.6)
, (1.6) .
. .
. , то получим первую теорему Кондратьева:
, то получим первую теорему Кондратьева:  , (11.2)
, (11.2) ,
,  .
.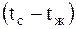 равной 1 градусу.
равной 1 градусу. между горячей средой и стенкой и
между горячей средой и стенкой и  между стенкой и холодной средой, т.е. задаётся закон теплообмена. Также задаётся коэффициент теплопроводности
между стенкой и холодной средой, т.е. задаётся закон теплообмена. Также задаётся коэффициент теплопроводности 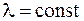 и толщина стенки δ.
и толщина стенки δ.
 , Дж.
, Дж.
 ,
,  (11.13)
(11.13) . (11.14)
. (11.14)
 ,
,  (11.15)
(11.15) , Вт.
, Вт. , (11.2)
, (11.2) ,
, 


