
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 11. Реальные газы. Явления переносаСодержание книги
Поиск на нашем сайте
Реальный газ – газ, где учитываются объем (размеры) и силы взаимодействия молекул. Учитывая собственный объем молекул и силы межмолекулярного взаимодействия, голландский физик И.Ван-дер-Ваальс введя поправки в уравнение Менделеева-Клайперона, вывел уравнение состояния реального газа. Уравнение состояния для 1 моля идеального газа имеет вид pV = RT Согласно этой формуле объем газа при сжатии может стать равным нулю. В случае реальных газов часть объема занята самими молекулами. Поэтому объем, занимаемый газом, должен быть уменьшен на величину b, где b - объем занимаемый самими молекулами, т.е. (V-b). Таким образом, b –постоянная величина, учитывающая объемы (размеры) молекул. где (p + pi), а – постоянная величина, учитывающая силы межмолекулярного притяжения
- уравнение Ван-дер-Ваальса для 1 моля газа
Величины a и b для различных газов различны и их значение приводятся в справочных таблицах.
Уравнение Ван-дер-Ваальса не единственное уравнение, описывающее реальные газы. Существуют и другие уравнения, некоторые из них даже точнее описывают реальные газы, но не рассматриваются из-за их сложности. Для исследования поведения реального газа рассмотрим изотермы Ван-дер-Ваальса – кривые зависимости давления p от объема V при заданных температурах Т, определяемые уравнение Ван-дер-Ваальса для 1 моля газа. Эти кривые рассматриваются для четырех различных температур и имеют своеобразный характер.
соответствует единственное значение объема, т.е. при высоких температурах вещество находится в однофазном – газообразном состоянии. Невысоким температурам соответствуют изотермы 2-, 3-, 4, на которых имеются изгибы.
Изобара AD пересекает изотерму 4 в трех точках А, В, С. Это означает, что вещество одновременно находится в трех фазовых состояниях. Переход от изотермы 5 к изотермам 4,3,2,1, соответствующий повышению температуры, приводит к тому, что изгибы на изотермах сглаживаются. Расстояние между точками А и С уменьшаются и на изотерме 2 сливаются в одну точку К. Здесь рК = const является касательной к изотерме. Эта изотерма называется критической, соответствующая температура Тк – критической, точка К – критической. Соответствующие этой точке VK и рК – называются критическими. Состояние с критическими параметрами (VK,,рК,,ТК) называются критическим состоянием. Температурам, выше критическим соответствует только газообразное состояние вещества. Следовательно, критическая температура ТК – это наивысшая температура, при которой газ может еще может быть превращен в жидкость. При критическом состоянии вещества различия в свойствах пара и жидкости отсутствуют. Критические состояния характеризуется непрерывным переходом пара в жидкость и жидкости в пар. Мы знаем, что U = U1 + U2 = Eк + Eр.
Работа сил молекулярного сцепления равна: dA = pi dV,
Мы знаем, что Тогда dU которое произошло за счет совершения работы
- потенциальная энергия
Тогда - внутренняя энергия 1 моля реального газа. Следовательно, внутренняя энергия реального газа зависит как от температуры, так и от его объема. В термодинамически неравновесных системах возникают особые необратимые процессы – явления переноса – в результате которых происходит пространственный перенос энергии, массы, импульса. К явлениям переноса относятся: 1. Теплопроводность обусловлена переносом энергии (горячий чай – холодная ложка). Если в одной области Ек молекул больше, чем в другой, то в процессе столкновений молекул с течением времени происходит выравнивание кинетической энергии, т.е. температур. Перенос энергии в форме теплоты подчиняется закону Фурье
jE – плотность теплового потока – энергия, переносимая в форме теплоты через единицу площади в единицу времени, перпендикулярную оси х.
2. Диффузия - самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и твердых тел. Явление диффузии подчиняется закону Фика
jm – плотность потока массы – масса вещества, диффундирующего в единицу времени через единицу площади, перпендикулярную оси х D – коэффициент диффузии
Согласно кинетической теории газов 3. Внутреннее трение (вязкость). Механизм возникновения внутреннего трения между параллельными слоями газа (жидкости), движущимися с различными скоростями заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, а движущегося медленнее – увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее. Сила трения между слоями подчиняется закону Ньютона
Тогда от одного слоя к другому передается импульс, по модулю равный действующей силе jp – плотность потока импульса – величина, определяемая полным импульсом, переносимым в единицу времени в положительном направлении оси х через единичную площадку, перпендикулярную оси х.
Динамическая вязкость определяется по формуле
Коэффициенты переноса связаны между собой соотношениями
Тема 12. Электростатика Еще в VII веке до нашей эры древнегреческий ученый Фалес обнаружил, что янтарь, потертый о шерсть, притягивает легкие предметы (расческа, электроскоп - примеры). Мы говорим, что тела наэлектризовываются или, тела при этом приобретают электрические заряды. Существуют два вида электрических зарядов: положительный «+» и отрицательный «-». Заряды одного знака – отталкиваются, а заряды разных знаков – притягиваются. Электрический заряд любой системы тел состоит из элементарных частиц. Элементарные частицы: электрон – несущий отрицательный элементарный заряд, протон – положительный элементарный заряд, нейтрон – заряд, которого равно нулю. qe = 1,6×10-19 Кл [q] = [Кл] = [А×с]; заряд электрона qe» заряду протона qпр, но масса протона mпр >2000 массы электрона me. q = Sq+ + Sq- - закон сохранения электрического заряда Из обобщения опытных данных установлено, что в изолированной системе алгебраическая сумма электрических зарядов остается постоянной – закон сохранения электрического заряда. Система называется электрически изолированной, если между ней и внешними телами нет обмена электрическими зарядами. Электрические заряды вокруг себя создают электрическое поле. Если же заряд неподвижен, то электрическое поле называется электростатическим. Точечным зарядом называется заряженное тело, размерами которого можно пренебречь по сравнению с расстоянием от этого тела до других тел, несущих заряд.
Закон взаимодействия неподвижных точечных электрических зарядов был экспериментально установлен французским физиком Кулоном. Сила, с которой взаимодействуют два точечных заряда, прямо пропорциональна произведению величин этих зарядов и обратно пропорциональна квадрату расстояния между этими зарядами
В системе СИ k =1/4 pe0 - коэффициент пропорциональности.
e0 = 8,85×10-12 Ф/м - электрическая постоянная Электрическое поле – особый вид материи, посредством которого взаимодействуют электрические заряды.
- силовая характеристика q0 пробныйточечныйзаряд электрического поля
- напряженность электрического поля
- напряженность электрического
где e - диэлектрическая проницаемость среды. Наглядно электрическое поле можно представить с помощью силовых линий. Линией напряженности электрического поля называется линия, в каждой точке которой касательная совпадает с вектором напряженности.
Энергетической характеристикой электрического поля является потенциал - отношение WР точечного электрического заряда, помещенного в рассматриваемую точку поля, к этому заряду q:
Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной. Определим работу, совершаемую силой F при перемещении точечного заряда из одной точки во вторую. 2 1 A = F×S
r 2 + q После преобразования r 1 А = qE (r1 –r2)
Известно, что A = -DWР т.е. работа по перемещению заряда в электростатическом поле равна убыли потенциальной энергии заряда q в рассматриваемом поле. Тогда
При перемещении электрического заряда в электростатическом поле работа сил поля равна произведению заряда на разность потенциалов начальной и конечной точек траектории движения заряда. Мы знаем, что A = FDr = qEDr С другой стороны A = -qDj Þ qEDr = -qDj
Изменение величины на единицу длины называется градиентом (grad) данной величины.
Е = - grad j - связь между силовой и энергетической характеристиками электрического поля. Поток вектора напряженности электрического поля – количество силовых линий, пронизывающих некоторую поверхность, расположенную перпендикулярно силовым линиям.
n N = E×Scos a - однородное поле a В случае неоднородного поля
dN = EdScos a
поток напряженности сквозь любую поверхность S равен алгебраической сумме потоков напряженности сквозь все малые участки этой поверхности. Единица измерения потока вектора напряженности электростатического поля
[ N ] = [ B×м ] Рассмотрим метод определения значения и направления вектора напряженности Е в каждой точке электростатического поля, создаваемого системой неподвижных зарядов q1,...qn. Экспериментально было установлено, что результирующая сила F, действующая со стороны электрического поля на пробный заряд q, равна
геометрической сумме сил Fi, приложенных к заряду q со стороны каждого из зарядов qi. Нам известно, что Fi = qEi где Еi – напряженность поля одного заряда qi
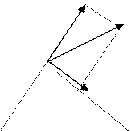
- принцип суперпозиции (наложения) электростатических полей. Напряженность электрического поля системы точечных зарядов равна сумме напряженностей полей каждого из этих зарядов в отдельности – принцип суперпозиции полей. Принцип суперпозиции позволяет рассчитать электрические поля любой системы неподвижных зарядов. Согласно принципу суперпозиции электрических полей можно найти напряженность в любой точке поля двух точечных зарядов +q1 и -q2
А по правилу параллелограмма.
вектора Е находится построением, а абсолютная величина определя +q1 · ·-q2 ется по формуле: Е = a - угол между Е1 и Е2 Вычисление Е поля системы электрических зарядов с помощью принципа суперпозиции можно упростить, используя теорему Гаусса, определяющую поток вектора напряженности электрического поля через произвольную замкнутую поверхность. Определим поток вектора напряженности через замкнутую поверхность (случай сферической поверхности радиусом r, окружающий один точечный заряд).
- теорема Остроградского - Гаусса
Поток вектора напряженности электрического поля сквозь произвольную замкнутую поверхность равен сумме, заключенных внутри этой поверхности зарядов, деленный на электрическую постоянную e0 - теорема Остроградского – Гаусса. Рассмотрим несколько случаев применения теоремы Остроградского – Гаусса для определения напряженности различных электростатических полей. Вначале введем понятие о плотности зарядов. Различают 3 вида: линейная, объемная и поверхностная плотности зарядов.
- при равномерном распределении заряда
- при равномерном распределении заряда
Окружим часть нити длиной l1, воображаемым l1 A цилиндром так, что боковая поверхность содержит точку А. r По теореме Остроградского - Гаусса
С другой стороны N = E×S = E×2prl1, где S = 2prl1 - площадь боковой части цилиндра.
Отсюда - напряженность поля, создаваемого бесконечно длинной равномерно заряженной нитью. 2. Определим напряженность поля, создаваемого бесконечно равномерно заряженной плоскостью в некоторой точке А.
А которого перпендикулярна плоскости, а правое основание содержит точку А. Плоскость делит цилиндр пополам. По теореме Остроградского – Гаусса
отсюда
3. Напряженность поля, создаваемого двумя бесконечно параллельными плоскостями, заряженными разноименно с одинаковыми плотностями.
бесконечными параллельными плоскостями равна сумме
пластинами.
Вне пластин вектора Е от каждой из них направлены в противоположные стороны и взаимно уничтожаются.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 348; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.40.40 (0.011 с.) |

 В реальных газах имеются силы взаимного притяжения молекул, которые действуют дополнительно к силам внешнего давления и как бы сжимают газ. Вследствие этого возникает добавочное внутреннее давление pi, т.е.
В реальных газах имеются силы взаимного притяжения молекул, которые действуют дополнительно к силам внешнего давления и как бы сжимают газ. Вследствие этого возникает добавочное внутреннее давление pi, т.е. Тогда, введя поправки на V и p, получим уравнение состояния реального газа
Тогда, введя поправки на V и p, получим уравнение состояния реального газа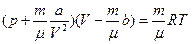 Для любой массы газа
Для любой массы газа
 В случае реального газа, помимо кинетической энергии Ек нужно учитывать потенциальную энергию Ер взаимодействия молекул.
В случае реального газа, помимо кинетической энергии Ек нужно учитывать потенциальную энергию Ер взаимодействия молекул. Внутренняя энергия для 1 моля идеального газа
Внутренняя энергия для 1 моля идеального газа Так как, то
Так как, то
 или интегрируя, получим:
или интегрируя, получим:


 - коэффициент теплопроводности
- коэффициент теплопроводности 
 – градиент температуры – изменение температуры на единицу длины. «-» - при теплопроводности энергия переносится в направлении убывания температуры.
– градиент температуры – изменение температуры на единицу длины. «-» - при теплопроводности энергия переносится в направлении убывания температуры.
 - градиент плотности, «-» показывает, что перенос массы происходит в направлении убывания плотности.
- градиент плотности, «-» показывает, что перенос массы происходит в направлении убывания плотности.


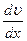 - градиент скорости, «-» - указывает, что импульс переносится в направлении убывания скорости.
- градиент скорости, «-» - указывает, что импульс переносится в направлении убывания скорости.
 и
и 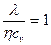
 :
: Тогда - закон Кулона
Тогда - закон Кулона
 Количественной характеристикой силового действия электрического поля является физическая величина – напряженность, определяемая формулой:
Количественной характеристикой силового действия электрического поля является физическая величина – напряженность, определяемая формулой: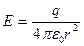 Пробный электрический заряд должен быть столь малым, чтобы его внесение в поле не вызывало изменения значений электрических зарядов.
Пробный электрический заряд должен быть столь малым, чтобы его внесение в поле не вызывало изменения значений электрических зарядов. точечного заряда в вакууме.
точечного заряда в вакууме. поля точечного заряда в среде.
поля точечного заряда в среде.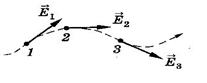

 Электрическое поле однородно, если во всех его точках векторы Е одинаковы, т.е. имеют одинаковую густоту.
Электрическое поле однородно, если во всех его точках векторы Е одинаковы, т.е. имеют одинаковую густоту.

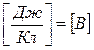
 q · · S = r1 –r2; F = qE
q · · S = r1 –r2; F = qE

 S N = E×S
S N = E×S

 Подставим значение силы F в предыдущую формулу и сократив на q, получим:
Подставим значение силы F в предыдущую формулу и сократив на q, получим:

 Сложение Е 1 и Е 2 производится
Сложение Е 1 и Е 2 производится Направление результирующего
Направление результирующего
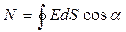
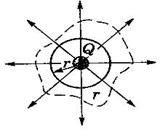
 Нам известно, что
Для сферической поверхности cosa = 1.
Нам известно, что
Для сферической поверхности cosa = 1.
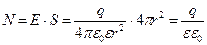 S = 4pr2 – площадь сферической поверхности
S = 4pr2 – площадь сферической поверхности
 Таким образом, из каждого точечного заряда выходит поток вектора напряженности, равный q/ee0. Если n зарядов, то
Таким образом, из каждого точечного заряда выходит поток вектора напряженности, равный q/ee0. Если n зарядов, то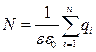

 Линейная плотность – физическая величина, характеризующая распреде-ление зарядов вдоль нити:
Линейная плотность – физическая величина, характеризующая распреде-ление зарядов вдоль нити: l – длина элемента нити.
l – длина элемента нити. Объемная плотность - физическая величина, характеризующая распреде-ление зарядов по объему:
Объемная плотность - физическая величина, характеризующая распреде-ление зарядов по объему:
 Поверхностная плотность - физическая величина, характеризующая рас-пределение зарядов по площади:
Поверхностная плотность - физическая величина, характеризующая рас-пределение зарядов по площади: - при равномерном распределении заряда по площади
- при равномерном распределении заряда по площади 1. Определим напряженность поля, создаваемого бесконечно длинной равномерно заряженной нитью (или цилиндром) в некоторой точке А на расстоянии r.
1. Определим напряженность поля, создаваемого бесконечно длинной равномерно заряженной нитью (или цилиндром) в некоторой точке А на расстоянии r.
 Приравнивая правые части, получим
Приравнивая правые части, получим
 Е Построим воображаемый цилиндр, ось
Е Построим воображаемый цилиндр, ось
 Также N = E×2S, приравнивая правые части, находим:
Также N = E×2S, приравнивая правые части, находим:
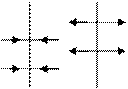 -s +s Напряженность поля между двумя
-s +s Напряженность поля между двумя напряженности полей, создаваемых обоими
напряженности полей, создаваемых обоими


