
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение отношения удельных теплоемкостей газа методом адиабатического расширенияСодержание книги
Поиск на нашем сайте
Ц е л ь р а б о т ы: определение показателя адиабаты для воздуха П р и б о р ы: стеклянный сосуд, ручной насос, манометр
Т е о р и я м е т о д а Изменение состояния идеального газа связано с изменением его параметров. Согласно 1 закона термодинамики, количество теплоты
Количество теплоты, необходимое для нагревания единицы массы вещества на один градус, называется удельной теплоемкостью:
Удельная теплоемкость газа зависит от условий, при которых происходит нагревание. Различают теплоемкости (удельную и молярную) при постоянном давлении (cp и
Отношение теплоемкостей газа при постоянном давлении и постоянном объеме
Процесс, при котором отсутствует теплообмен между системой и окружающей средой, называется адиабатным, т.е. В случае адиабатного процесса из уравнения (1): 1) 2)
ющей среды Через некоторое время газ нагреется вследствие теплообмена до температуры окружающей среды
Подставляя отношение объемов из уравнения (6) в уравнение (5) получим Прологарифмируем это выражение и найдем показатель адиабаты
Так как значения давления мало отличаются друг от друга, в первом приближении разность логарифмов заменим разностью самих величин:
П о р я д о к р а б о т ы
1. Убедиться, что уровни воды в манометре доведены до нулевого уровня. 2. Закрыть кран и нагнетать воздух в баллон до тех пор, пока разность уровней воды в манометре не достигнет 200 мм. 3. Выждать, пока уровни воды в манометре не установятся. Отсчитать установившуюся разность уровней 4. Быстро открыть кран и как только уровни воды в манометре сравняются – закрыть кран. Когда давление окончательно установится, замерить новую разность уровней в манометре 5. Опыт повторить 7-9 раз. Вычислить по формуле (7) Результаты занести в таблицу. Таблица
Контрольные вопросы 1. Определение удельной и молярной теплоемкости. 2. 1-начало термодинамики и его применение к изопроцессам. 3. Какой процесс называется адиабатным? Уравнение Пуассона. 4. 1-начало термодинамики в случае адиабатного процесса. 5. Вычислить показатель адиабаты для одно-, двух-, трехатомного газа.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 345; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.114.199 (0.008 с.) |

 , сообщенное системе, идет на увеличение внутренней энергии системы
, сообщенное системе, идет на увеличение внутренней энергии системы  и на совершение термодинамической работы
и на совершение термодинамической работы 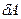
 (1)
(1) (2)
(2) ) и при постоянном объеме (cv и
) и при постоянном объеме (cv и  ). Для жидких и твердых тел, объем которых мало изменяется по сравнению с газом, значения
). Для жидких и твердых тел, объем которых мало изменяется по сравнению с газом, значения  и
и  близки друг к другу по величине. Для разного рода практических расчетов их можно считать одинаковым. Сообщенное при постоянном давлении тепло идет на совершение работы и на изменение внутренней энергии, а при постоянном объеме – только на изменение внутренней энергии. Поэтому
близки друг к другу по величине. Для разного рода практических расчетов их можно считать одинаковым. Сообщенное при постоянном давлении тепло идет на совершение работы и на изменение внутренней энергии, а при постоянном объеме – только на изменение внутренней энергии. Поэтому  , а их отношение больше единицы и зависит от количества атомов, составляющих молекулу. Теплоемкости могут быть выражены через степени свободы молекул (число независимых переменных, полностью определяющих положение системы в пространстве):
, а их отношение больше единицы и зависит от количества атомов, составляющих молекулу. Теплоемкости могут быть выражены через степени свободы молекул (число независимых переменных, полностью определяющих положение системы в пространстве): (3)
(3) играет в термодинамике важную роль. В частности, оно входит в уравнение Пуассона, которое описывает адиабатный процесс.
играет в термодинамике важную роль. В частности, оно входит в уравнение Пуассона, которое описывает адиабатный процесс. (4)
(4)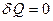 .
. - работа внешних сил увеличивает внутреннюю энергию газа.
- работа внешних сил увеличивает внутреннюю энергию газа. - газ совершает работу за счет убыли внутренней энергии системы
- газ совершает работу за счет убыли внутренней энергии системы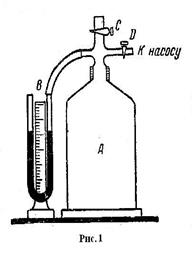
 , а давление
, а давление  , где
, где  - атмосферное давление,
- атмосферное давление,  - избыточное давление, измеряемое разностью уровней жидкости в манометре. Таким образом, первое состояние газа определяется параметрами
- избыточное давление, измеряемое разностью уровней жидкости в манометре. Таким образом, первое состояние газа определяется параметрами  . Если открыть кран на короткое время, то воздух будет расширяться до объема
. Если открыть кран на короткое время, то воздух будет расширяться до объема  , давление упадет до атмосферного
, давление упадет до атмосферного  . Это будет второе состояние. Процесс перехода из состояния 1 в состояние 2 протекает очень быстро, поэтому его можно считать адиабатным. Согласно уравнению Пуассона
. Это будет второе состояние. Процесс перехода из состояния 1 в состояние 2 протекает очень быстро, поэтому его можно считать адиабатным. Согласно уравнению Пуассона  или
или  (5)
(5) , где
, где  -новая разность уровней жидкости в манометре. Это новое третье состояние газахарактеризуется параметрами
-новая разность уровней жидкости в манометре. Это новое третье состояние газахарактеризуется параметрами  . Так как в первом и третьем состояниях температура одинакова, то параметры этих состояний можно связать уравнением Бойля-Мариотта:
. Так как в первом и третьем состояниях температура одинакова, то параметры этих состояний можно связать уравнением Бойля-Мариотта: или
или  (6)
(6)


 или
или  (7)
(7)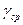 и ошибки.
и ошибки.



