
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение движения тел по наклонной плоскостиСодержание книги
Поиск на нашем сайте
Л а б о р а т о р н а я р а б о т а № 3 ИЗУЧЕНИЕ ДВИЖЕНИЯ ТЕЛ ПО НАКЛОННОЙ ПЛОСКОСТИ Ц е л ь р а б о т ы: определение скорости движения тел на наклонной плоскости и сравнение теоретических результатов с экспериментальными. П р и б о р ы: наклонная плоскость, шар, цилиндр, линейка, ящик с песком. Т е о р и я м е т о д а Рассмотрим движение тела по наклонной плоскости длиною
По закону сохранения энергии где υ - линейная скорость, ω - угловая скорость тела, J – момент инерции тел, h - высота наклонной плоскости. Теоретическая скорость υТ определяется из соотношения (1). Для этого угловая скорость заменяется линейной с учетом формулы После постановки w и Jш, Jц в уравнение (1), получаем расчётные формулы скорости шара и цилиндра
Измерив высоту наклонной плоскости, вычисляем теоретические значения скоростей в точке В. Экспериментальное определение скорости проводят так. В точке В тело имеет скорость υ, которая может быть представлена в виде двух компонент υх и υу – скорости в горизонтальном и вертикальном направлениях Из законов поступательного движения находим х = Время движения в обоих направлениях одинаково и равно Подставив время (4) в уравнение (3), получим выражение для экспериментальной скорости в точке В
а по найденному выражению скорости, окончательно находим время
Порядок работы 1. Измерить длину ℓ наклонной плоскости, высоту h и основание b, вычислить 2. Пустить тело из точки Aпо наклонной плоскости и измерить расстояние: х = СД и у = ВС 3.Вычислить экспериментальное значение скорости по формуле (5) и сравнить со значением теоретической скорости, вычисленной по формуле (2). По формуле (6) вычислить время движения. Опыт повторить три раза при разных высотах. Данные занести в таблицу.
Контрольные вопросы 1. Сформулировать и записать закон сохранения и превращения энергии в данной работе. 2. Дать определение и записать формулу мгновенной скорости, указать направление. 3. Что характеризует нормальное, тангенциальное и полное ускорение и чему они равны? 4. Вывести формулу экспериментальной и теоретической скоростей.
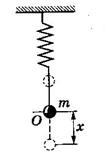
Л а б о р а т о р н а я р а б о т а № 5 ИЗУЧЕНИЕ СОБСТВЕННЫХ КОЛЕБАНИЙ ПРУЖИННОГО МАЯТНИКА Ц е л ь р а б о т ы: изучение упругих колебаний П р и б о р ы: пружина, набор грузов, штатив, линейка, секундомер Т е о р и я м е т о д а Колебания – движения или процессы, характеризующиеся определенной повторяемостью во времени. Колебания, происходящие за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему, называются свободными или собственными. Колебания считаются периодическими, если система приходит в положение равновесия через равные промежутки времени. Простейшими периодическими колебаниями являются гармонические, в которых смещение тела или системы от положения равновесия совершается по закону синуса или косинуса. Груз массой m, подвешенный на упругой пружине и совершающий гармонические колебания под действием упругой силы Fупр = -kx представляет собой пружинный маятник.
То же самое будет при отклонении маятника вверх, но природа силы будет иная. Это– равнодействующая силы тяжести и (не полностью компенсирующей ее) силы упругости пружины. По величине эта равнодействующая пропорциональна величине смещения x от положения равновесия маятника. Таким образом, возвращающая сила, действующая на отклоненный маятник - это сила квазиупругая, равная по закону Гука Fупр = - kx, (1) где k – коэффициент упругости или жесткость пружины. Тогда по II закону Ньютона - kx = m где m – масса маятника, a = Преобразовав это уравнение к виду и представив Решением этого дифференциального уравнения является функция
х = А sin (w0t+j0) или х = А сos (w0t + j0) (5)
Формула (5) выражает смещение х пружинного маятника в любой момент времени t и является кинематическим уравнением гармонического колебания в общем виде. А – амплитуда -. максимальное отклонение от положения равновесия (w0t + j0) – фаза - величина, определяющая положение колеблющейся системы в любой момент времени t j0 – начальная фаза колебания, определяющая положение системы в начальный момент времени t = 0 w0 – круговая (циклическая) частота - количество полных колебаний за 2 p секунды Время одного полного колебания - период Т Число полных колебаний, совершаемых в единицу времени – частота колебания ν. Они связаны Т = Учитывая, что w02 = Выясним физический смысл коэффициента упругости k: k = - где Fq - внешняя деформирующая сила, в соответствии с III- законом Ньютона Fq = -Fупр. Следовательно, коэффициент упругости k численно равен внешней силе, вызывающей деформацию пружины, равную единице длины. Свободные колебания, амплитуда которых из–за потерь энергии реальной колебательной системой с течением времени уменьшается, называются затухающими. Такие колебания совершаются при одновременном действии силы упругости Fупр= - kх и силы сопротивления Fс = - r× u где r – коэффициент сопротивления среды, u - скорость колеблющейся системы. Динамическое дифференциальное уравнение затухающих колебаний решением которого является кинематическое уравнение:
х = А0е -bt× sin(wt+j0) (9)
А0 – начальная амплитуда при t = 0 е - основание натурального логарифма b = w - циклическая частота свободных затухающих колебаний. Величины циклических частот затухающих и незатухающих колебаний связаны соотношением w2 = w20 - b2. Амплитуда при затухающих свободных колебаниях уменьшается с течением времени по экспоненциальному закону: Аt = A0e -bt (10) Скорость затухания колебательного движения характеризуется декрементом затухания, который равен отношению двух последующих амплитуд, разделенных интервалом времени, равным одному периоду колебания (рис. 2) d = Натуральный логарифм этого отношения называется логарифмическим декрементом затухания: l = ln Определив опытным путем период затухающих колебаний можно вычислить коэффициент затухания b и логарифмический декремент затухания l. Для этого измеряют две амплитуды, отстающие во времени на n периодов, т.е. t = nT. Равенство отношений следовательно ln Отсюда коэффициент затухания b = Порядок работы
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 386; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.204.52 (0.008 с.) |

 (рис.1). Тело, скатываясь с наклонной плоскости, участвуют в поступательном и вращательном движениях.
(рис.1). Тело, скатываясь с наклонной плоскости, участвуют в поступательном и вращательном движениях. рис.1.
рис.1. По закону сохранения энергии, по-тенциальная энергия уменьшается и переходит в кинетическую энергию. В точке В тело приобрело кинетическую энергию поступа-тельного движения
По закону сохранения энергии, по-тенциальная энергия уменьшается и переходит в кинетическую энергию. В точке В тело приобрело кинетическую энергию поступа-тельного движения  и вращательного движения
и вращательного движения 
 (1)
(1) , а момент инерции шара и цилиндра выражается формулами
, а момент инерции шара и цилиндра выражается формулами 

 ,
, 
 (2)
(2)

 у =
у =  (3)
(3) (4)
(4)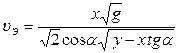 (5)
(5)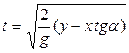 (6)
(6) и
и 





 (2)
(2) - ускорение, равное второй производной смещения по времени.
- ускорение, равное второй производной смещения по времени. (3)
(3) w02, получим динамическое уравнение свободных незатухающих гармонических колебаний
w02, получим динамическое уравнение свободных незатухающих гармонических колебаний 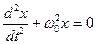 (4)
(4)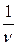 w0 = 2p n
w0 = 2p n получим период колебаний пружинного маятника Т = 2p
получим период колебаний пружинного маятника Т = 2p  (6)
(6) (7)
(7) (8)
(8) - коэффициент затухания j0 – начальная фаза
- коэффициент затухания j0 – начальная фаза (11)
(11) (12)
(12)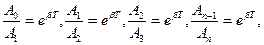 позволяет записать
позволяет записать  (13)
(13) (14)
(14) (15)
(15)


