
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение показателя адиабаты для воздуха
Л а б о р а т о р н а я р а б о т а № 18 ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ АДИАБАТЫ ДЛЯ ВОЗДУХА
Ц е л ь р а б о т ы: определить показатель адиабаты акустическим методом. П р и б о р ы: звуковой генератор, трубка со встроенными на концах телефоном и микрофоном, осциллограф, усилитель низкой частоты.
Теория метода
Причиной звуковых ощущений у людей и животных является воздействие на их органы слуха упругих волн, распространяющихся в воздухе или в другой упругой среде. Звук может распространяться только в среде (газ, жидкость, твердое тело). Скорость звука зависит от упругих свойств среды. Звук возникает в среде при колебании какого-нибудь тела (струны или частиц). Если бросить камень на поверхность воды, то пойдут круги или как мы говорим волны. Точка, куда упал камень, является источником возмущения. Возмущение передается в различные участки поверхности воды посредством волны. Звук не может распространяться в вакууме, так как там нет вещества, которое через себя передавало бы возмущение от одной частицы к другой по цепочке. Распространение волн не связано с переносом вещества. Волны бывают поперечными и продольными. Волна на поверхности воды есть пример поперечной волны. Если колебание частиц среды перпендикулярно распространению волны - волна называется поперечной. Колебания мембраны в телефоне создают колебания среды, т.е. чередование областей сжатия и разряженности в пространстве образуют волну. Это есть пример продольных упругих волн. В зависимости от частоты колебаний различают два вида распространения колебаний: изотермический и адиабатический. При очень малых частотах процесс сжатия и расширения происходит изотермически. А при больших частотах наблюдается адиабатическое сжатие и расширения воздуха. Сжатие происходит так быстро, что нет оттока теплоты в окружающую среду, а при расширении воздух охлаждается и не успевает нагреться за счет притока теплоты извне. Поэтому процесс, происходящий в воздухе будет адиабатическим. Уравнение адиабатического процесса рVγ = сonst. Это уравнение называется еще и уравнением Пуассона, где γ- коэффициент Пуассона, равный отношению удельных или молярных теплоемкостей газа при постоянном давлении и постоянном объеме
γ = Ср/Сv. Скорость звука в среде определяется формулой
или дифференцируя уравнение Пуассона, получим:
откуда
тогда скорость звука будет равна Используя уравнение состояния найдем Подставляя в формулу (7) значение р определяем скорость звука
Звуковой генератор вырабатывает сигналы звуковой частоты от 20-2000 Гц. Этот сигнал подаем на телефон. Телефон преобразует электрические колебания в механические колебания мембраны. Излучаемый звук направляется во внутрь трубки, на другом конце которой расположен микрофон. Падающий на плоский микрофон звук отражается обратно и взаимодействует с падающей волной. При определенных условиях, когда внутри трубки укладывается целое число полуволн, образуется стоячая волна- застывшая картина волны. Микрофон преобразует обратно звуковые колебания в электрические. Эти сигналы усиливаются усилителем и подаются на вход осциллографа для визуального наблюдения сигнала. Перемещая микрофон вдоль трубки мы можем наблюдать изменения амплитуды сигналов на осциллографе.
ЗГ УНЧ ОСЦ.
Рис 1.
В тот момент, когда микрофон попадает в узел стоячей волны, наблюдается минимум сигнала, а когда микрофон перемещаясь попадает в пучность стоячей волны, будет наблюдаться максимум сигнала. Но можно сделать опыт иначе. Не перемещая микрофон, увеличивая частоту сигнала мы можем добиться укладки вдоль трубки целого количества полуволн
ℓ - длина трубки. Можно найти две «соседние» частоты при котором наблюдается максимум сигнала на осциллографе. Этим частотам соответствуют пучности на микрофоне. Для двух частот имеем два значения длин волн λ 1 и λ 2.
Найдем разницу частот: Подставляя значение из формулы (10) имеем
Отсюда найдем Зная молекулярный вес воздуха μ = 0,029 кг/моль, температуру воздуха, длину трубки и разность частот, мы можем найти γ - показатель адиабаты.
Порядок работы 1. Собрать схему (рис 1.) 2. Линейкой измерить длину трубки 5 раз и занести в таблицу
3. Измерить температуру воздуха вдоль трубки снаружи в 5 местах. 4. Включить усилитель. Ручка «усиление» устанавливается в крайнее левое положение. 5.Включить осциллограф. Ручка «усиление» устанавливается по у в крайнее левое положение. Ручка «усиление» по Х в крайнее правое положение, делитель 1: 1. 6. Включить звуковой генератор ЗГ-18. Ручка «усиление» должна быть в крайнем левом положении. Подать на телефон сигнал звуковой частоты около 700 Гц с напряжением 5 В. 8. Регулируя ручками «усиление» на УНЧ и осциллографе, добьемся четкого изображения синусоиды с амплитудой 3-4 см на экране осциллографа. 9. Подбирая частоту, вращением ручки «частота» на звуковом генераторе, добьемся максимума амплитуды на экране осциллографа. 10. Записать частоту ν 1 в таблицу. Вращая ручку «частота» на ЗГ-18 в ту же сторону найдем значение частоты ν2, при котором будет наблюдаться максимум амплитуды.Частоту ν 2 занесем в таблицу. Пункты 9 и 10 повторить 3 раза. 11. Найти среднее значение Т и занести в таблицу Т = 273 + t 0C По формуле (16) вычислить γ. 12. Оценить погрешности измерения. Таблица
Контрольные вопросы 1.Звук, изотермический и адиабатический способы передачи звука 2.Условие образования стоячей волны. Меняется ли частота звука при переходе из одной среды в другую? 3.Что называется теплоемкостью? Удельные и молярные теплоемкости. 4.Как выражаются теплоемкости при постоянном объеме и давлении от степени свободы молекул? Вывести формулу Майера. 5.Как запишется первое начало термодинамики для адиабатического процесса?
Лабораторная работа 5.1.1.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 182; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.93.207 (0.015 с.) |
 , где k – модуль объемной упругости среды из закона Гука
, где k – модуль объемной упругости среды из закона Гука (3)
(3)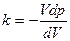 (4)
(4)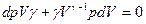 (5)
(5) (6)
(6) (7)
(7) (8)
(8) (9)
(9)
 (10)
(10)









 телефон микрофон
телефон микрофон , где k = 1,2,3,4,…… (11)
, где k = 1,2,3,4,…… (11)


 , где
, где  (12)
(12)
 (13)
(13)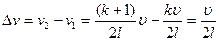 (14)
(14) (15)
(15) (16)
(16)


