
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Крестовины вместе с муфтами.Содержание книги
Поиск на нашем сайте 1. Расположить муфты на расстоянии R от оси вращения и установив грузы на высоте h измерить время падения t. Вычислить по формулам (5) и (6) моменты инерции системы и только муфт. Опытное значение момента инерции муфт (6) сравнить с теоретическим значением, вычисленным по формуле (7). 2. Изменив расстояние R, повторить опыт и данные занести в таблицу 2. 3. Оценить расхождение между теоретическими и экспериментальными данными, определив относительную ошибку в процентах.
4. Полученные результаты занести в таблицу 2. Таблица 2
Контрольные вопросы Напишите и сформулируйте основной закон динамики вращательного движения. Дать определения момента инерции, момента силы. 2. Получить рабочую формулу (5). 3. Как определить момент инерции крестовины не снимая с нее грузов? 4. При любом ли расположении грузов на крестовине их можно считать точечными?
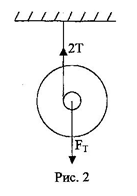
Л а б о р а т о р н а я р а б о т а № 9 ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАЯТНИКА МАКСВЕЛЛА Ц е л ь р а б о т ы: научиться составлять уравнения для поступатель-ного и вращательного видов движения П р и б о р ы: маятник Максвелла, штангенциркуль. Теория метода Маятник Максвелла представляет собой массивный диск (1) жёстко посаженный на вал (2). Концы вала подвешены на нитях (3) одинаковой длины. Если намотать нити на вал, то маятник поднимется на некоторую высоту h. При отключении электромагнита вал, вращаясь вместе с диском, будет опускаться, а нити будут разматываться. Достигнув нижнего положения, система поднимается вверх, наматывая нити в обратную сторону. Удерживают маятник в верхнем положении электро-
На маятник действуют две силы: сила тяжести FT, направленная вертикально вниз и сила упругости двух нитей 2Т (рис.2). Напишем второй закон Ньютона для поступательного и вращательного движения применительно к маятнику Максвелла. FT – 2Т = ma (1) М = J ε (2)
Из формулы (1) найдем 2Т 2Т = FT – ma = mg – ma = m(g-a) (5) Подставляя в формулу (4) значение 2Т имеем m(g-a)r = J ε (6) Используя связь между линейным и угловым ускорениями a = r ε откуда m(g-a) r = Из этого уравнения найдём момент инерции маятника J
Пройденный путь при равноускоренном движении определяется из уравнения s = υ0 t + Пройденный путь равен длине нити или высоте h. Учитывая, что начальная скорость υ0 = 0 имеем Подставляя значение ускорения в уравнение (7) найдём окончательное выражение для момента инерции маятника Максвелла
С энергетической точки зрения колебания маятника Максвелла в вертикальной плоскости происходят в результате перехода потенциальной энергии маятника Еп = mgh в кинетическую энергию поступательного и вращательного движения Ек + Евр. = и наоборот. В данной работе также определяют силу сопротивления, исходя из закона сохранения энергии следующим образом: если считать, что первоначально маятник находился на высоте h1, а спустя период поднялся на высоту h2 (h2 < h1 из-за сил сопротивления движению), то изменение потенциальной энергии будет равна работе сил сопротивления: mgh1- mgh2 = Fc(h1+ h2) Отсюда найдем
Порядок работы
1. С помощью штангенциркуля измерить радиус вала r. 2. Определить массу маятника m. Масса маятника находится сложением массы вала, массы диска и массы обода: m = mB + mD + mO Массы этих частей написаны на деталях в граммах. 3. Аккуратно вращая вал, намотать нити на вал (при этом маятник находится на высоте h 1). 4. Нажать на кнопку ПУСК и измерить время падения с помощью секундомера. 5. Определить высоту поднятия маятника h 2. 6. Опыт повторить 5 раз. 7. Вычислить момент инерции маятника (10) и силу сопротивления (11). 8. Результаты эксперимента и вычислений занести в таблицу. Таблица
Контрольные вопросы 1. Дайте определение моменту сил М и момента инерции J. 2. Почему при вычислении момента сил мы берем силу 2Т, а не mg? 3. Какая связь между линейной и угловой скоростями и ускорениями? 4. Получить расчетную формулу момента инерции маятника. 5. Как определяют силу сопротивления?
Л а б о р а т о р н а я р а б о т а №10
ОПРЕДЕЛЕНИЕ СКОРОСТИ ПОЛЕТА СНАРЯДА
Ц е л ь р а б о т ы: применение законов сохранения момента импульса и энергии, для расчета скорости полета снаряда П р и б о р ы: крутильно-баллистический маятник Т е о р и я м е т о д а
Знак «-» означает, что крутящий момент направлен противоположно направлению закручивания. В результате тело будет совершать гармонические колебания. Кинетическая энергия маятника
По основному закону динамики для вращательного движения крутящий момент М равен М = J×e (3) J - момент инерции e - угловое ускорение, равное второй производной от угла поворота. e = j ² Приравнивая уравнения (1) и (3) получим J×e = - kj или J×e +kj = 0. Заменяя e на j ², получим J j ² + k × j или j ²+ Маятник будет совершать колебания с периодом Т = 2p Колебания маятника начнутся после попадания снаряда в него. Момент импульса снаряда передается маятнику, т.е. переходит в момент импульса маятника m× u× r = Jwmax (5) m – масса снаряда u – скорость снаряда r - расстояние от точки попадания снаряда до центра вращения. Из формулы (5) выражаем скорость полета снаряда u = Таким образом, для вычисления скорости полета снаряда необходимо измерить массу снаряда m и расстояние r от точки попадания снаряда до центра вращения. Момент инерции маятника J и угловую скорость wmax определяем следующим образом:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 521; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.01 с.) |


 рис. 1.
рис. 1.
 подставляя значение ε в уравнение (6) получим
подставляя значение ε в уравнение (6) получим r или m (g-a) r2 = J a (7)
r или m (g-a) r2 = J a (7)
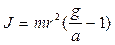 (8)
(8)
 (9)
(9)
 (10)
(10) +
+ 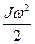
 (11)
(11)
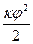
 =
= 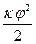 (2)
(2) × j = 0. Это уравнение описывает гармоническое колебательное движение, а
× j = 0. Это уравнение описывает гармоническое колебательное движение, а  следовательно
следовательно 

 (6)
(6)


