
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3. Принцип относительности в механикеСтр 1 из 21Следующая ⇒
Если системы отсчета движутся относительно друг друга прямолинейно и равномерно, и в одной из них справедливы законы Ньютона – инерциальные системы отсчета. Во всех инерциальных системах отсчета законы классической динамики имеют одинаковую форму - суть механического принципа относительности (принцип относительности Галилея).
Определим связь между координатами точки А в обеих системах r = r1 + r0 = r1 + u × t В проекциях на оси координат:
Y = y1 + u y t - преобразования координат Галилея Z = z1 + uzt В классической механике ход времени не зависит от относительного движения систем отсчета, тогда можно записать t = t1 Преобразования Галилея справедливы только при u << с, а при u @ с – заменяются преобразованиями Лоренца.
Ускорение Таким образом, ускорение точки А в системе отсчета К и К1, движущихся равномерно друг относительно друга прямолинейно и равномерно одинаково.
При u @ с преобразования Галилея несправедливы. Нужно было создать новую механику, которая содержала бы ньютоновскую механику как предельный случай для малых скоростей (u<< с). Это удалось, сделать А. Эйнштейну – он заложил основы специальной теории относительности. Специальная теория относительности также называется релятивистской теорией. В основе специальной теории относительности лежат постулаты Эйнштейна: принцип относительности: все законы природы инвариантны по отношению к переходу от одной инерциальной системы относительности к другой, т.е. любые физические явления протекают одинаково во всех инерциальных системах отсчета. принцип инвариантности скорости света: скорость света в вакууме предельна и одинакова во всех инерциальных системах отсчета.
y1 = y
При малых скоростях преобразования Лоренца переходят в преобразования Галилея – принцип соответствия. Следствия из преобразования Лоренца: 1. Координаты х, х 1 и время t, t 1 не могут быть мнимыми, т.е. подкоренное выражение должно быть больше нуля. Следовательно, u/с <<1, т.е. u относительного движения двух инерциальных систем отсчета не может превосходить с.
4. Длина тел
Таким образом, длина, измеренная в системе, относительно которой он движется, оказывается меньше длины измеренной в системе, относительно которой стержень покоится. 5. Пусть скорость тела внутри ракеты – u 1, ракета имеет скорость u по отношению к Земле. Определим скорость u движения тела с точки зрения земного наблюдателя. Тогда релятивистский закон сложения скоростей:
Следовательно Мы знаем, законы Ньютона выполняются в инерциальных системах отсчета. Системы отсчета, движущиеся относительно инерциальной системы с ускорением, называется неинерциальными. В неинерциальных системах отсчета законы Ньютона несправедливы. Но можно применить, если кроме сил обусловленных воздействием тел друг на друга, ввести в рассмотрение силы особого рода – силы инерции. Если учесть силы инерции, то II закон Ньютона будет справедлив для любой системы отсчета. В данном случае ma 1 =F+F ин, т.е. произведение массы тела на его ускорение равно сумме всех сил, действующих на тело, включая F ин. F ин должны быть такими, чтобы вместе с силами F, обусловленными воздействием тел друг на друга, они сообщали телу ускорение a 1, каким оно обладает в неинерциальной системе отсчета. Так как F = ma (а -ускорение тела в инерциальной системе отсчета), то m a 1 = ma + F ин. Силы инерции обусловлены ускоренным движением системы отсчета относительно измеряемой системы.
Тема 4. Работа и энергия Что значит, с точки зрения физики совершить работу? Допустим, что тело М под действием силы F перемещается по прямой в направлении этой силы. Величина
При F = const если a > 0 A > 0 если a - тупой угол А < 0 если a = 900 А = 0 В случае переменной силы F выделяем элементарный участок dS, на котором силу F можно считать постоянной.
dS S2 Элементарная работа a · dA = F dS cosa
А полная работа на участке S1S2 FH S1 · Чтобы вычислить работу А, построим график зависимости F от S.
- мгновенная мощность
Þ
Способность тела совершить работу характеризуется физической величиной – энергия.
Кинетическая энергия – энергия движения
- потенциальная энергия упруго деформированного тела
При переходе тела или системы тел из одного состояния в другое совершается работа, которая служит мерой изменения энергии, обусловливающего этот переход. Если работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений, то такие силы называются консервативными. Если же работа совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипативной (сила трения). Полная энергия системы
Wк + Wp = W = const – закон сохранения и превращения энергии
В системе тел, между которыми действуют только консервативные силы, энергия остается постоянной. В системе, в которой действуют также диссипативные (неконсервативные) силы энергия системы не сохраняется.
Тема 5.Твердое тело в механике Вращательное движение – это движение, при котором все точки тела движутся по окружности, и центр окружности расположен на одной прямой, называемой осью вращения. При вращательном движении положение тела в любой момент времени определяется углом поворота j радиуса вектора R любой точки тела относительно своего начального положения [ j ] - [ рад ].
- мгновенная угловая скорость при
- угловая скорость при равномерном
движении. Dj = 2p - угол, соответствующий одному полному обороту тела. Dt = T – соответствующее время или период обращения. Если вращение тела происходит неравномерно, то быстроту изменения угловой скорости характеризуют угловым ускорением
Направление угловой скорости определяется по правилу буравчика: направление вектора угловой скорости совпадает с направлением поступательного движения буравчика, рукоятка которого вращается вместе с телом. 1) w = const, j = wt - равномерное движение
2) e > 0 - равноускоренное движение
3) e < 0 - равнозамедленное движение
Вращение тела вызывает только сила F, являющаяся касательной к окружности. Силу F – называют вращающей силой. Действие силы F зависит не только от её значения, но и от расстояния точки её приложения А до оси вращения, т.е. зависит от момента силы. Моментом силы называется произведение вращающей силы F на радиус окружности r, описываемой точкой приложения силы M = F×r - момент силы [ H×м ]
Моментом инерции материальной точки относительно некоторой оси, называется произведение массы материальной точки на квадрат расстояния до этой оси. J = m×r2 - момент инерции [ кг×м2 ] Момент инерции характеризует инертность тела при вращательном движении.
- момент инерции шара с радиусом R
- момент инерции цилиндра
- момент инерции стержня
Во всех перечисленных примерах ось вращения проходит через центр масс тела. Момент инерции относительно любой произвольной оси, не проходящей через центр масс, определяется по теореме Штейнера: J = J0 + md2 Момент инерции относительно любойпроизвольной оси, не проходящей черезцентр тяжести равен сумме момента инерции относительно параллельнойоси, проходящей через центр тяжести и произведению массы на квадратрасстояния между этими осями. II закон Ньютона – основной закон динамики поступательного движения F = ma Умножив обе стороны уравнения на r, получим: F×r = mar Причем, а = e×r, Fr = M, mr2 = J
Следовательно, М = J×e - основное уравнение динамики вращательного движени я или II закон Ньютона для вращательного движения.
- основной закон динамики вращательного движения. MDt – импульс момента сил (импульс вращающегося момента). L = Jw - момент импульса (момент количества движения).
Тогда аналогично закону сохранения импульса
- закон сохранения момента импульса
Катящийся без скольжения шар совершает вращательное и поступательное движения одновременно. И полная энергия равна
Wк = Wпост + Wвращ или
Таким образом, мы выяснили, что S,u,a, t – кинематические характеристики поступательного движения j,w,e, t – кинематические характеристики вращательного движения F, m, p - динамические характеристики поступательного движения M, J, L - динамические характеристики вращательного движения Тема 6. Физика колебаний Колебательные процессы – процессы, характеризующиеся определенной повторяемостью во времени. Колебания называются свободными (или собственными) если они совершаются за счет первоначально сообщенный энергии при последующем отсутствии внешних воздействий. Вынужденные колебания совершаются под действием внешней периодически изменяющейся силы, которая называется вынуждающей.. Простейшим типом колебаний являются гармонические колебания – колебания, совершающиеся по закону синуса или косинуса. х = A sin (wt + j); х = A cos (wt + j) - уравнение гармонических колебаний
w - круговая или циклическая частота, число полных колебаний за 2p секунд. t – время; j - начальная фаза – определяет положение колеблющегося тела в начальный момент времени при t = 0.
Т – период - время одного полного колебания; [ с ]
[ Гц ] - частота колебаний – число полных колебаний за 1с.
w = 2pn - связь между циклической частотой и частотой колебания Скорость гармонических колебаний определим как производную смещения:
a = - w2x – ускорение гармонических колебаний.
- дифференциальное уравнение гармонических колебаний. Решением этого уравнения является выражение х = A sin (wt + j).
Потенциальная энергия материальной точки, совершающей гармонические колебания под действием упругой силы F
Полная энергия остается постоянной, так как при гармонических колебаниях справедлив закон сохранения механической энергии, поскольку упругая сила консервативна.
Гармоническим осциллятором называется система, совершающая колебания, описываемые уравнением вида: х¢¢ + w2х =0 Примерами гармонического осциллятора является пружинный, физический и математические маятники. Пружинный маятник – это груз массой m, подвешенный на упругой пружине и совершающей гармонические колебания под действием упругой силы
Математический маятник – система, состоящая из материальной точки массой m, подвешенной на нерастяжимой, невесомой нити и колеблющаяся под действием силы Fm.. Момент инерции математического маятника
маятника,период колебаний которого совпадает с периодом колебаний данного физического маятника. Колеблющееся тело может участвовать в нескольких колебательных процессах, тогда необходимо найти результирующее колебание, т.е. колебания необходимо сложить. Сложим гармонические колебания одного направления и одинаковой частоты.
х2 = A2 cos (wt + j2) Тогда уравнение результирующегоколебания х = х1 + х2 = A соs (wt + j) Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает так же гармонические колебания в том же направлении и с той же частотой. Амплитуда результирующего колебания зависит от разности фаз (j2 - j1) складываемых колебаний.
Период биений w - разность частот складываемых колебаний. Теперь рассмотрим результат сложения двух гармонических колебаний одинаковой частоты, происходящих во взаимных перпендикулярных направлениях вдоль оси x и y.
- уравнение эллипса Так, как траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными. Если частоты складываемых взаимно перпендикулярных колебаний различны, то замкнутая траектория результирующего колебания сложная. Замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два взаимно – перпендикулярных колебания, называются фигурами Лиссажу. Фигуры Лиссажу
здесь d = const, - коэффициент затухания. где r – коэффициент сопротивления. Решением уравнения в случае малых затуханий (d2 << w2) является х = А0е-dt cos (wt+j) где А = А0е-dt – амплитуда затухающих колебаний А0 – начальная амплитуда.
Промежуток времени, в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации.
Тогда период затухающих колебаний
- декремент затухания, а его логарифм
- логарифмический декремент затухания N e – число колебаний, совершаемых за время уменьшения амплитуды в е раз. Чтобы получить в реальной колебательной системе незатухающие колебания, надо компенсировать потери энергии. В случае механических колебаний нужна внешняя вынуждающая сила F = F0 coswt. Тогда уравнение вынужденных колебаний
где
Чтобы определить резонансную частоту wрез – частоту, при которой амплитуда достигает максимума – нужно найти максимальную функцию или минимальную подкоренного выражения. Продифференцировав подкоренное выражение по частоте, получим: wрез =
Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте называют резонансом. При d2 << w02, значение резонансной частоты wрез совпадает с w0, тогда
Тема 7. Механические волны Процесс распространения колебаний в среде называется волновым процессом или волной. Основное свойство всех волн – перенос энергии без переноса вещества. Волны бывают продольные и поперечные. В продольных волнах частицы среды колеблются в направлении распространения волны. В поперечных волнах – в плоскостях, перпендикулярных направлению распространения волны. Продольные волны возникают при деформации сжатия и растяжения, поперечные волны возникают при деформации сдвига. Волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими.
Расстояние между ближайшими точками, колеблющимися в одинаковой фазе называют длиной волны - l - [ м ]
Скорость распространения волн тем меньше, чем больше её плотность - r. Скорость продольной волны: Скорость поперечной волны:
где Е - модуль упругости или модуль Юнга; s - модуль сдвига. ® u l ний. Волны от источника колебания распро- страняются вдоль прямой. Уравнение колебаний точки В задано хВ = Аsinwt = Аsin2pn Точка С повторяет колебания точки В с некоторым запозданием. Тогда уравнение точки С хС = Аsin2pn(t-t)
Тогда х = А sin2pn (t - l/u) или учитывая, что
- уравнение бегущей волны.
Бегущими называются волны, которые переносят в пространстве энергию. Существуют еще стоячие волны – волны, образующиеся при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами. Волны, распространяющиеся в любой среде и имеющие частоту в пределах от 16-20 до 20000 Гц, называются звуковыми волнами, которые воспринимает человеческое ухо. Волны с частотой n< 16 Гц – инфразвуки, а с частотой n >20 кГц – ультразвуки. Основными характеристиками звука являются высота, сила (интенсивность) и тембр звука. Высота звука определяется частотой колебаний. Чем больше частота колебаний, тем выше звук.
Сила звука – энергетическая характеристика звуковой волны и мы субъективно оцениваем как громкость звука. Для каждой частоты колебаний существует наименьшая - порог слышимости и наибольшая – порог болевого ощущения интенсивность звука, которая способна вызвать звуковое восприятие. Область между этими двумя порогами – область слышимости. Тембр звука – оттенок или окраска звуковых колебаний.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 230; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.172.252 (0.21 с.) |

 X = x1 + uxt
X = x1 + uxt Известно - правило сложения скоростей в классической механике.
Известно - правило сложения скоростей в классической механике.
 Следовательно, при переходе от одной инерциальной системы отсчета к другой уравнения динамики не изменяются, т.е. являются инвариантными по отношению к преобразованиям координат.
Следовательно, при переходе от одной инерциальной системы отсчета к другой уравнения динамики не изменяются, т.е. являются инвариантными по отношению к преобразованиям координат. Эйнштейн показал, что в теории относительности классические преобразования Галилея заменяются преобразованиями Лоренца, которые имеют вид:
Эйнштейн показал, что в теории относительности классические преобразования Галилея заменяются преобразованиями Лоренца, которые имеют вид: z1 = z
z1 = z
 2. События, происходящие одновременно в разных местах системы К при наблюдении их из системы К 1, движущейся относительно К, могут казаться разновременными – нарушение одновременности удаленных событий
2. События, происходящие одновременно в разных местах системы К при наблюдении их из системы К 1, движущейся относительно К, могут казаться разновременными – нарушение одновременности удаленных событий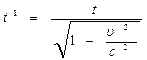 3. Интервал времени становится функцией скорости системы
3. Интервал времени становится функцией скорости системы

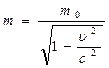 6. Относительность масс
6. Относительность масс Тогда основной закон динамики
Тогда основной закон динамики - релятивистский импульс
- релятивистский импульс
 FT
FT F
F

 Величина, характеризующая скорость выполнения работы, называется мощностью [ Bт ]
Величина, характеризующая скорость выполнения работы, называется мощностью [ Bт ] Если мощность изменяется с течением времени, то
Если мощность изменяется с течением времени, то Вместо dA подставим ее значение и получим
Вместо dA подставим ее значение и получим
 Различают два вида механической энергии: W к и W р.
Различают два вида механической энергии: W к и W р.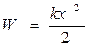 Потенциальная энергия Wp – энергия взаимодействия – энергия, обусловленная взаимным расположением тел или частей и характером их взаимодействия W = mgh
Потенциальная энергия Wp – энергия взаимодействия – энергия, обусловленная взаимным расположением тел или частей и характером их взаимодействия W = mgh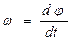

 Угол j - угловой путь при вращательном движении. При вращательном движении угловая скорость - w.
[ w ] –
Угол j - угловой путь при вращательном движении. При вращательном движении угловая скорость - w.
[ w ] –
 неравномерном движении.
неравномерном движении.



 - угловая скорость при равноускоренном движении.
- угловая скорость при равноускоренном движении.
 Моменты инерции разных симметричных тел массой m:
Моменты инерции разных симметричных тел массой m:

 Угловое ускорение
Угловое ускорение
 Тогда, умножив обе стороны уравнения на Dt получим следующее:
Тогда, умножив обе стороны уравнения на Dt получим следующее:
 При вращательном движении кинетическая энергия определяется по формуле
При вращательном движении кинетическая энергия определяется по формуле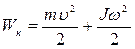


 Кроме того, колебания ёще характеризуются периодом и частотой колебаний.
Кроме того, колебания ёще характеризуются периодом и частотой колебаний.

 Ускорение
Ускорение Тогда запишем
Тогда запишем Кинетическая энергия материальной точки, совершающей гармонические колебания
Кинетическая энергия материальной точки, совершающей гармонические колебания
 Тогда полная энергия гармонических колебаний
Тогда полная энергия гармонических колебаний
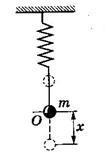
 Потенциальная энергия пружинного маятника
Потенциальная энергия пружинного маятника



 Физический маятник – твердое тело, совершающее под действием силы тяжести колебания, вокруг неподвижной оси, не проходящей через центр тяжести.
- период колебаний физического маятника.
где J - момент инерции,
l- расстояние между точкой подвеса и центром тяжести
- приведенная длина физического маятника
Физический маятник – твердое тело, совершающее под действием силы тяжести колебания, вокруг неподвижной оси, не проходящей через центр тяжести.
- период колебаний физического маятника.
где J - момент инерции,
l- расстояние между точкой подвеса и центром тяжести
- приведенная длина физического маятника
 Тогда
Тогда
 .
период колебаний математического маятника
Если L = l, то периоды колебаний одинаковы.
Следовательно, приведенная длина физического маятника – эта длина такого математического
.
период колебаний математического маятника
Если L = l, то периоды колебаний одинаковы.
Следовательно, приведенная длина физического маятника – эта длина такого математического
 х1 = A1 соs (wt + j1)
х1 = A1 соs (wt + j1) Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называется биением.
Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называется биением.

 х = A соs wt
y = В cos (wt + j)
Сложив эти два уравнения и сделав преобразования, получим:
х = A соs wt
y = В cos (wt + j)
Сложив эти два уравнения и сделав преобразования, получим:

 Рассмотрим свободные затухающие колебания, амплитуда которых из-за потерь энергии колебательной системой с течением времени уменьшается. Уменьшение энергии происходит вследствие трения в механических колеба-тельных системах и превращение её в теплоту (пружинный маятник).
Рассмотрим свободные затухающие колебания, амплитуда которых из-за потерь энергии колебательной системой с течением времени уменьшается. Уменьшение энергии происходит вследствие трения в механических колеба-тельных системах и превращение её в теплоту (пружинный маятник).


 Затухание нарушает периодичность колебаний, поэтому затухающие колебания не являются периодическими и к ним не применимо понятие периода или частоты. Если затухание мало, то можно условно пользоваться понятием периода – как промежутка времени между двумя последующими максимумами (или минимумами) колеблющейся физической величины.
Затухание нарушает периодичность колебаний, поэтому затухающие колебания не являются периодическими и к ним не применимо понятие периода или частоты. Если затухание мало, то можно условно пользоваться понятием периода – как промежутка времени между двумя последующими максимумами (или минимумами) колеблющейся физической величины. Если А(t) и А(t+T) - амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающихся на период, то отношение
Если А(t) и А(t+T) - амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающихся на период, то отношение


 Решение уравнения равно сумме решения однородного уравнения и частного решения
Решение уравнения равно сумме решения однородного уравнения и частного решения



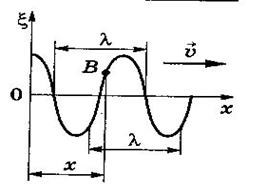 Гармоническая поперечная волна
Гармоническая поперечная волна



 Пусть в точке В находится источник колеба-
Пусть в точке В находится источник колеба- Точка В колеблется в течение времени t. Эти колебания дойдут до точки С через время t, поэтому время колебаний точки С – (t-t). Расстояние от точки В до точки С, равное l, волна проходит со скоростью
Точка В колеблется в течение времени t. Эти колебания дойдут до точки С через время t, поэтому время колебаний точки С – (t-t). Расстояние от точки В до точки С, равное l, волна проходит со скоростью Отсюда
Отсюда


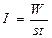 Силой (интенсивностью) звука называется величина, определяемая энергией, переносимой звуковой волной в единицу времени сквозь единичную площадку, перпендикулярную направлению распространения волны.
Силой (интенсивностью) звука называется величина, определяемая энергией, переносимой звуковой волной в единицу времени сквозь единичную площадку, перпендикулярную направлению распространения волны.


