
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Упражнение 1 Определение коэффициента упругости пружины
1.На шкале отметить первоначальное нулевое положение конца подвешенной пружины х0 = 0 без платформы. 2.Подвесить платформу массой mпл и положить на платформу добавочный груз массой m1. По шкале определить абсолютное удлинение пружины х1. 3.Повторить опыт с добавочными грузами m2 и m3, измеряя соответствующие удлинения пружины х2 и х3. 4. Вычислить деформирующие силы: F1= (mпл+m1) g F2= (mпл+m2)g F3= (mпл+m3) g где g @ 9,8 м/c2 – ускорение свободного падения. 5.Вычислить для каждой деформирующей силы коэффициент упругости пружины k 1, k2, k3, по формуле: k1 = 6. Определить среднее значение коэффициента упругости пружины kcр = 7. Результаты измерения и вычисления занести в таблицу 1. Таблица 1.
Упражнение 2 Определение периода собственных колебаний 1.Подвесить платформу массой mnл и положить на платформу добавочный груз массой m1. 2.Зафиксировать положение равновесия нагруженного маятника, оттянув маятник приблизительно на 1 см, отпустить вместе с пуском секундомера. Измерить время t тридцати полных колебаний (n = 30). 3.Опыт повторить с добавочными грузами m2 и m3, измеряя время t2 и t3 для n = 30. 4.На лабораторных весах определить массу пружины mпр. 5.Вычислить период колебаний T = 6.Вычислить расчетную величину периода колебаний по формуле (6) Т0 = 2 kср - среднее значение коэффициента упругости (упр. 1). 7.Сравнить полученные результаты: 8.Результаты измерения и вычисления занести в табл. 2.
Таблица 2
Упражнение 3 Определение логарифмического декремента Затухания пружинного маятника 1.Подвесить платформу массой mпл и положить на нее добавочный груз массой ml, использованный в упр.2. 2.Зафиксировать положение равновесия нагруженного маятника 3.Оттянув пружину с грузом на А0 = (4 6) см вниз отпустить маятник вместе с пуском секундомера и считать число полных колебаний по моментом возвращения маятника в нижнее положение максимального отклонения. Отсчитать 50 полных колебаний. Остановить секундомер при счете «50» и одновременно зафиксировать по шкале соответствующую амплитуду А50.
4.Опыть повторить для грузов с массами m2, m3 (упр. 2). 5.Вычислить: а) период колебаний: Т = б) циклическую частоту: w = в) коэффициент затухания b = г) коэффициент сопротивления среды: r = 2mb д) логарифмический декремент затухания: l = bТ Результаты измерения и вычисления занести в таблицу 3. Таблица 3
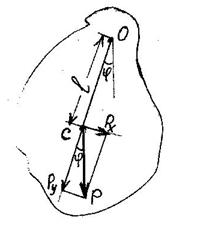
Контрольные вопросы 1. Что называют свободными колебаниями? 2. Какие колебания называются гармоническими? Записать уравнение. 3. Получить дифференциальные и кинематические уравнения свободных гармонических и затухающих колебаний. 4. Объяснить по графику х = f (t) затухающих колебаний закон убывания амплитуды. 5. Физический смысл логарифмического декремента затухания. Л а б о р а т о р н а я р а б о т а № 6 ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТРАКТОРНОГО ШАТУНА Ц е л ь р а б о т ы: расчет момента инерции тел неправильной формы П р и б о р ы: тракторный шатун, линейка, секундомер, острая подставка Т е о р и я м е т о д а Физическим маятником называется твердое тело, способное совершать колебания под действием силы тяжести вокруг неподвижной оси, не проходящей вокруг центра тяжести (рис.1). Вращение твердого тела характеризуется моментом силы, моментом инерции и угловым ускорением, которые связаны между собой М = J × e (1) Момент инерции твердого тела есть мера его инертности при вращательном движении и измеряется суммой произведений масс точек тела на квадраты их расстояний до оси вращения J = Для тел правильной геометрической формы момент инерции вычисляется интегрированием. Для тел неправильной геометрической формы – экспериментально. Примером физического маятника является тракторный шатун.
Если физический маятник отклонить на угол j, то на него будут действовать сила тяжести Р в центре тяжести С и сила реакции опоры N в точке 0. Ввиду того, что векторы этих сил не направлены по одной прямой, действие их не скомпенсировано. Если спроектировать силу тяжести на оси х и у, то проекция Рх является возвращающей силой, момент которой равен
Приравнивая значение моментов сил (уравнения (1) и (3)) получим дифференциальное уравнение второго порядка: J Произведение Тогда Т=2p и момент инерции будет равен J = относительно оси, проходящей через точку 0. По теореме Штейнера определяем момент инерции относительно центра тяжести С: J =Jc + md2 где d = l, J c = J – md2
Порядок работы
1. Определить положение C центра тяжести тракторного шатуна, положив его поперек острой подставки. 2. Измерить расстояние от точки подвеса до центра тяжести ℓ. 3. Измерить массу шатуна m. 4. Определить время 30 полных колебаний и рассчитать период 5.Повторить опыт три раза и найти среднее значение tср и Т ср 6. Рассчитать значение момента инерции тракторного шатуна относи- тельно точки 0 и точки С. Все данные занести в таблицу: Таблица:
Определить относительную ошибку в процентах: d = ( Контрольные вопросы
1. Какой маятник называется физическим? 2. Что характеризует момент инерции в каких единицах измеряется? 3. Как формулируется теорема Штейнера? 4. Получить расчетную формулу момента инерции тракторного шатуна.
Л а б о р а т о р н а я р а б о т а № 8
ИЗУЧЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТЕЛ
Ц е л ь р а б о т ы: Определение момента инерции вращающихся грузов и сравнение экспериментальных данных с теоретическими П р и б о р ы: Крестообразный маятник с набором муфт, штангенциркуль, секундомер, линейка, груз. Т е о р и я м е т о д а Вращательное движение твердого тела характеризуется углом поворота j, угловой скоростью
Основное уравнение динамики вращательного движения выражает связь между М, J,
Угловое ускорение e может быть найдено, если измерить h и время падения t груза
здесь r - радиус шкива, на которую наматывают нить. Из уравнения поступательного движения груза определим силу натяжения нити (силой трения пренебрегаем) ma = mg – T Тогда вращательный момент М равен: M = T× r = m(g-a)r (4) Таким образом из уравнений (1), (2), (4) получаем экспериментальную формулу для определения момента инерции маятника
Момент инерции муфт находят опытным путем как разность моментов инерции системы (крестовины вместе с муфтами) J и крестовины без муфт J0 Jм = J - J0 (6) Размеры муфт малы по сравнению с расстоянием R от оси вращения до центров масс грузов, поэтому теоретическое значение моментов инерции муфт равно J¢M = 4m1R2 (7) где m1 -масса одной муфты. Порядок работы Упражнение 1. Определение момента инерции крестовины без муфт 1. Измерить радиус шкива r и массу опускающегося груза m. 2. Установить груз на высоту h и предоставляя возможность грузу па-дать, измерить время падения секундомером t. 3. Вычислить момент инерции крестовины J0 по формуле (5). Таблица 1
Упражнение 2. Определение момента инерции системы –
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 278; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.22.250 (0.049 с.) |
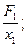 k2 =
k2 = 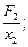 k3 =
k3 = 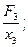
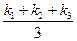
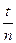
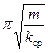 , где m = mпр+mпл+mгруз;
, где m = mпр+mпл+mгруз;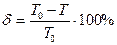
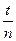
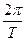 (с-1)
(с-1)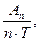 (с-1)
(с-1)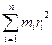 (2)
(2)
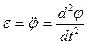
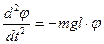 Þ
Þ 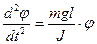
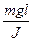 равно квадрату угловой скорости w2. Угловая скорость связана с периодом обращение Т =
равно квадрату угловой скорости w2. Угловая скорость связана с периодом обращение Т = 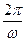
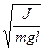
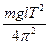
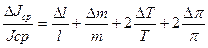 )×100%
)×100%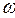 , угловым ускорением
, угловым ускорением 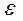 , вращательным моментом
, вращательным моментом 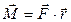 и моментом инерции
и моментом инерции 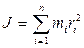 где
где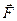 -действующая сила,
-действующая сила, 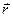 -радиус вектор, mi –масса любой точки тела.
-радиус вектор, mi –масса любой точки тела.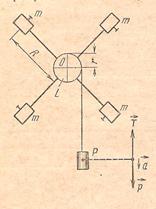 рис.1.
рис.1.
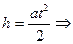


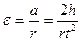 (2)
(2)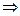 T = mg – ma = m (g - a) (3)
T = mg – ma = m (g - a) (3)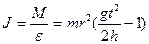 Þ
Þ 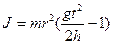 (5)
(5)


