Линия зацепления, угол зацепления, коэффициент перекрытия. Понятие об эвольвенте.

Линия зацепления - Траектория общей точки контакта зубьев при её движении относительно неподвижного звена зубчатой передачи, которая при линейном контакте определяется в главном сечении передачи.

Примечание
При отсутствии указаний линия зацепления соответствует теоретическим поверхностям взаимодействующихзубьев.

угол зацепления- Угол между линией зацепления и прямой, перпендикулярной к межосевой линии.

коэффициент перекрытия- Отношение угла осевого перекрытия зубчатого колеса косозубой цилиндрической передачи к его угловому шагу

Понятие об эвольвенте

Понятие об эвольвенте

 

К зацеплению предъявляют три основных требования:

1. Во все фазы зацепления окружные скорости точек колёс должны быть постоянными, то есть должно выполняться условие U = const;

2. Направление усилия, действующего на зуб, должно быть постоянным;

3. Колёса должны быть взаимозаменяемыми и допускать погрешность в межосевом расстоянии.

Этим условиям наиболее полно удовлетворяет эвольвентное зацепление.

Эвольвентой окружности называется кривая, описываемая точкой, лежащей на прямой, обкатываемой по окружности без скольжения (рис. 3.2).

Прямая, обкатываемая по окружности, называется производящей прямой. Окружность, по которой обкатывается производящая прямая, называется основной окружностью и обозначается d_В.

Свойства эвольвенты:

1. Нормаль к эвольвенте в любой точке является касательной к основной окружности.

2. Длина отрезка АВ нормали к эвольвенте равна длине дуги АВ₀ основной окружности.

3. Точка А основной окружности есть центр кривизны эвольвенты в точке В.

Основная теорема зацепления

 

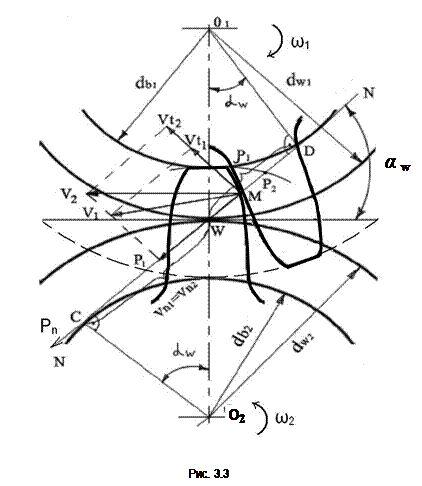
Рассмотрим эвольвентное зацепление (рис. 3.3). NN – общая нормаль двух эвольвент и для той и другой является производящей прямой, таким образом, во все фазы зацепления точка контакта лежит на прямой NN, поэтому линия NN называется линией зацепления.

Угол между линией зацепления и нормалью к линии, соединяющей центры колёс, называется углом зацепления a_W.

Точка “W” пересечения линии зацепления и линии, соединяющей центры колёс, называется полюсом зацепления. Видно, что во все фазы зацепления полюс остаётся на месте. Участок линии зацепления Р₁Р₂, заключённый между окружностями головок зубьев, называется активным участком линии зацепления.

Проведём векторы скоростей точек М (М₁; М₂) зацепления V₁ и V₂ (они проводятся перпендикулярно своим радиусам - векторам в точке М). Из схемы разложения в прямоугольной системе координат скоростей V₁ и V₂ видно, что нормальная работа зацепления возможна только при V_n1 = V_n2:

 

Откуда или

т. е. первое условие выполнено.

Последнее равенство называется основной теоремой зацепления. Эта теорема может быть сформулирована так: нормаль в точке соприкосновения элементов высшей пары качения и скольжения делит линию центров на части, обратно пропорциональные угловым скоростям.

Важно отметить, что в точке W нет взаимного скольжения зубьев, т. е.

Это означает, что в процессе работы зацепления окружности с диаметрами d_W1 и d_W2 обкатываются без скольжения. Эти окружности называются начальными.

Из подобия и следует, что . Отсюда следует важное соотношение .

Усилие в зацеплении направлено по общей нормали, то есть по линии зацепления, и, значит, постоянно по направлению (второе условие).

 

Элементы геометрии эвольвентного зацепления

 

Рассмотрим следующую модель. Имеем весьма твёрдую зубчатую рейку и заготовку зубчатого колеса из абсолютно неупругого материала (рис. 3.4). Отметим на рейке плоскость, называемую делительной, на которой толщина зуба равна ширине впадины. На заготовке отметим цилиндр d, а на рейке – касательную к нему плоскость (начальную плоскость), параллельную делительной плоскости.

Сообщим заготовке и рейке такое движение, при котором цилиндр d катится без скольжения по начальной плоскости рейки. В результате пластического деформирования на заготовке образуются зубья, причём при плоских боковых сторонах зубьев изделия имеют эвольвентный профиль.

Цилиндр d, являющийся начальным цилиндром в движении рейки относительно зубчатого колеса, называется делительным цилиндром, а окружность d – делительной окружностью.

Элементы зубчатых колёс стандартизованы. В качестве основного параметра принят модуль зубьев m – величина, пропорциональная шагу P_t по делительному цилиндру, т. е.

. (3.1)

 

В России модули стандартизированы в диапазоне от 0,05 до 100 мм.

Окружной делительный шаг P_t – это расстояние между одноимёнными профилями соседних зубьев, измеренное по дуге делительной окружности зубчатого колеса. Очевидно , где z – число зубьев, откуда . Подставляя последнее выражение в уравнение (3.1), получим

.

Из рис. 3.3 видно, что радиусы кривизны профилей в полюсе

ρ₁ = DW и ρ₂ = СW, тогда из и следует, что