
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы науки «Сопротивление материалов».Содержание книги
Поиск на нашем сайте
Сопротивление материалов 1. Понятия и определения, которыми оперирует наука «Сопротивление материалов». Сопротивление материалов – наука о прочности, жесткости и надежности элементов инженерных конструкций. Методами сопротивления материалов ведутся практические расчеты и определяются необходимые, как говорят, надежные размеры деталей машин, различных конструкций и сооружений. Основные понятия сопротивления материалов опираются на законы и теоремы общей механики и в первую очередь на законы статики, без знания которых изучение данного предмета становится практически невозможным. В отличие от теоретической механики сопротивление материалов рассматривает задачи, где наиболее существенными являются свойства деформируемых тел, а законы движения тела, как жесткого целого, не только отступают на второй план, но в ряде случаев являются попросту несущественными. Сопротивление материалов имеет целью создать практически приемлемые простые приемы расчета типичных, наиболее часто встречающихся элементов конструкций. Необходимость довести решение каждой практической задачи до некоторого числового результата заставляет в ряде случаев прибегать к упрощающим гипотезам – предположениям, которые оправдываются в дальнейшем путем сопоставления расчетных данных с экспериментом. Необходимо отметить, что первые заметки о прочности упоминаются в записках известного художника ЛЕОНАРДО Де ВИНЧИ, а начало науки о сопротивлении материалов связывают с именем знаменитого физика, математика и астронома ГАЛИЛЕО ГАЛИЛЕЯ. В 1660 году Р.ГУК сформулировал закон, устанавливающий связь между нагрузкой и деформацией: «Какова сила – таково и действие». В XVIII веке необходимо отметить работы Л.ЭЙЛЕРА по устойчивости конструкций. XIX – XX века являются временем наиболее интенсивного развития науки в связи с общим бурным ростом строительства и промышленного производства при безусловно огромном вкладе ученых-механиков России. Введем основные понятия, принимаемые при изучении дисциплины. Прочность – это способность конструкции выдерживать заданную нагрузку, не разрушаясь. Жесткость – способность конструкции к деформированию в соответствие с заданным нормативным регламентом. Деформирование – свойство конструкции изменять свои геометрические размеры и форму под действием внешних сил Устойчивость – свойство конструкции сохранять при действии внешних сил заданную форму равновесия. Надежность – свойство конструкции выполнять заданные функции, сохраняя свои эксплуатационные показатели в определенных нормативных пределах в течение требуемого промежутка времени. Ресурс – допустимый срок службы изделия. Указывается в виде общего времени наработки или числа циклов нагружения конструкции. Отказ – нарушение работоспособности конструкции. Опираясь на вышесказанное, можно дать определение прочностной надежности. Прочностной надежностью называется отсутствие отказов, связанных с разрушением или недопустимыми деформациями элементов конструкции. На рис.1 приведена структура модели прочностной надежности. Она включает известные модели или ограничения, которые априорно накладываются на свойства материалов, геометрию, формы изделия, способы нагружения, а также модель разрушения. Инженерные модели сплошной среды рассматривают материал как сплошное и однородное тело, наделенное свойством однородности структуры. Модель материала наделяется свойствами упругости, пластичности и ползучести.
Рис.1. Структура модели прочностной надежности элементов конструкций Упругостью называется свойство тела восстанавливать свою форму после снятия внешних нагрузок. Пластичностью называется свойство тела сохранять после прекращения действия нагрузки, или частично полученную при нагружении, деформацию. Ползучестью называется свойство тела увеличивать деформацию при постоянных внешних нагрузках. Основными моделями формы в моделях прочностной надежности, как известно, являются: стержни, пластины, оболочки и пространственные тела (массивы), рис.2. Модели
Рис.2. Основные модели формы в моделях прочностной надежности: а) стержень, б) пластина, в) оболочка
нагружения содержат схематизацию внешних нагрузок по величине, характеру распределения (сосредоточенная или распределенная сила или момент), а также воздействию внешних полей и сред. Внешние силы, действующие на элемент конструкции, подразделяются на 3 группы: 1) сосредоточенные силы, 2) распределенные силы, 3) объемные или массовые силы. Сосредоточенные силы — силы, действующие на небольших участках поверхности детали (например давление шарика шарикоподшипника на вал, давление колеса на рельсы и т.п.) Распределенные силы приложены значительным участкам поверхности (например давление пара в паропроводе, трубопроводе, котле, давление воздуха на крыло самолета и т.д. Объемные или массовые силы приложены каждой частице материала (например силы тяжести, силы инерции) После обоснованного выбора моделей формы, материала, нагружения переходят к непосредственной оценке надежности с помощью моделей разрушения. Модели разрушения представляют собой уравнения, связывающие параметры работоспособности элемента конструкции в момент разрушения с параметрами, обеспечивающими прочность. Эти уравнения (условия) называют условиями прочности. Обычно рассматриваются в зависимости от условий нагружения четыре модели разрушения: статического разрушения, длительно статического разрушения, малоциклового статического разрушения, усталостного разрушения. При малом числе циклов (N<102) развиваются значительные пластические деформации (статическое разрушение), при большом числе циклов (N>105) пластические деформации отсутствуют (усталостное разрушение). В промежуточной области (102<N<105) разрушение носит смешанный характер (малоцикловое разрушение). Если на элемент конструкции действует высокая температура (для алюминиевых сплавов свыше 200 Co, для стальных и титановых сплавов свыше 400 Co, для жаропрочных сплавов свыше 600 Co), но в этом случае рассматривается так называемая длительная прочность материала. Таким образом, сопротивление материалов зависит не только от величин действующего усилия, но и от длительности самого воздействия. Напряжения. Напряжением называется интенсивность действия внутренних сил в точке тела, то есть, напряжение — это внутреннее усилие, приходящееся на единицу площади. По своей природе напряжение — это поверхностная нагрузка, возникающая на внутренних поверхностях соприкасания частей тела. Напряжение, так же как и интенсивность внешней поверхностной нагрузки, выражается в единицах силы, отнесенных к единице площади: Па=Н/м2 (МПа = 106 Н/м2, кгс/см2=98 066 Па ≈ 105Па, тс/м2 и т. д.).
Рассечем тело произвольным сечением. Выделим небольшую площадку ∆A. Внутреннее усилие, действующее на нее, обозначим  . Полное среднее напряжение на этой площадке . Полное среднее напряжение на этой площадке  . Найдем предел этого отношения при ∆ A . Найдем предел этого отношения при ∆ A  0. Это и будет полным напряжение на данной площадке (точке) тела. 0. Это и будет полным напряжение на данной площадке (точке) тела.
Полное напряжение p Касательное напряжение, в свою очередь, может быть разложено на две составляющие, параллельные координатным осям x, y, связанным с поперечным сечением –
Отметим, что в дальнейшем будем иметь дело главным образом не с полным напряжением p Тензор напряжений
Компоненты напряжений по трем перпендикулярным граням элемента образуют систему напряжений, описываемую специальной матрицей – тензором напряжений
Здесь первый столбец представляет компоненты напряжений на площадках, нормальных к оси x, второй и третий – к оси y и z соответственно. При повороте осей координат, совпадающих с нормалями к граням выделенного элемента, компоненты напряжений изменяются. Вращая выделенный элемент вокруг осей координат, можно найти такое положение элемента, при котором все касательные напряжения на гранях элемента равны нулю. Площадка, на которой касательные напряжения равны нулю, называется главной площадкой. Рис. 2.1
Во всех случаях, однако, система внешних сил образует равнодействующую F, направленную вдоль оси стержня. Поэтому независимо от условий крепления растянутого стержня, расчетная схема в рассматриваемых случаях (рис. 2.1, а, б) оказывается единой (рис. 2.1, в) согласно принципу Сен – Венана. Если воспользоваться методом сечений (рис. 2.2), то становится очевидным, что во всех поперечных сечениях стержня возникают нормальные силы N z, равные силе F (рис. 2.2, б). Сжатие отличается от растяжения, формально говоря, только знаком силы N z. При растяжении нормальная сила N z направлена от сечения (рис. 2.2, б), а при сжатии – к сечению.
Рис. 2.2
Растягивающие продольные силы принято считать положительными ( рис. 2.3, а), а сжимающие – отрицательными (рис. 2.3, б).
Рис. 2.3
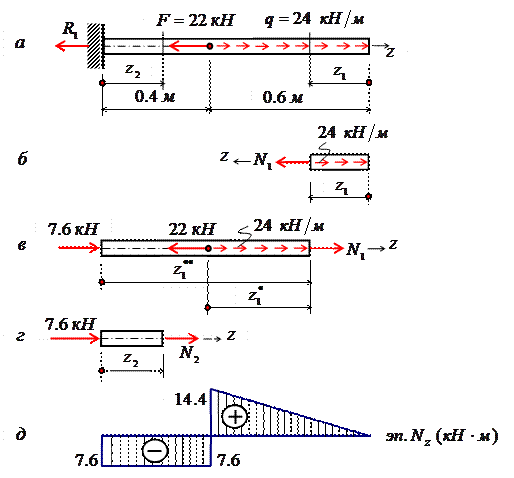
Вместе с тем между растяжением и сжатием могут обнаружиться и качественные различия, как, например, при изучении процессов разрушения материала или при исследовании поведения длинных и тонких стерж-ней, для которых сжатие сопровождается, как правило, изгибом. При расчете стержней, испытывающий деформацию растяжения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от N z), возникающих в стержне, и нахождение линейных перемещений в зависимости от внешней нагрузки. Продольные силы (N z), возникающие в поперечных сечениях стержня, определяются по внешней нагрузке с помощью метода сечений. График, показывающий изменение продольных сил по длине оси стержня, называется эпюрой продольных сил (эп. N z). Он дает наглядное представление о законе изменения продольной силы. Осью абсцисс служит ось стержня. Каждая ордината графика – продольная сила (в масштабе сил) в данном сечении стержня. Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти N max при растяжении-сжатии). Сечение, где действует максимальное усилие будем называть опасным. Перед построением эпюр необходимо освободить брус, в котором будем строить эпюры от опорных связей (выделить объект равновесия) и приложить к нему все действующие внешние силы (активные и реактивные). Затем необходимо установить границы участков, в пределах которых закон изменения внутренних сил постоянный. Границами таких участков являются сечения, где приложены сосредоточенные силы или начинается и кончается распределенная нагрузка, а также сечения, где имеется перелом стержня. Применяя метод сечений и учитывая правила знаков изложенные выше, получаем уравнения изменения внутренних сил в пределах длины каждого участка бруса. Затем, используя, полученные зависимости строим графики (эпюры) этих усилий. Ординаты эпюр в определенном масштабе откладываем от базисной линии, которую проводим параллельно оси бруса. Рассмотрим стержень постоянного поперечного сечения, жестко защемленный правым концевым сечением и нагруженный заданной внешней сосредоточенной нагрузкой F и распределенной q (рис. 2.4, а). Прежде всего определим опорную реакцию R 1, задавшись ее направлением вдоль оси z. Σ F z=0, - R 1 - 22 + 24∙0,6 = 0, R 1= -7,6 кН. Знак минус говорит о том, что действительное направление опорной реакции R 1 противоположно показанному на рис. 2.4, а. Исправляем его и в дальнейших расчетах знак минус у опорной реакции R 1 не учитываем (рис. 2.4, в, г). Под участком будем понимать часть стержня, на которой N z представляется некоторым аналитическим выражением. На другом участке N z будет определяться другой функцией. Границами участка являются начало и конец стержня, сечения, где приложены сосредоточенные нагрузки, начинается и заканчивается распределенная нагрузка. В нашем случае стержень разбивается на два участка. В пределах первого участка мысленно рассечем стержень на две части нормальным сечением (рис. 2.4, б, в).
Рис. 2.4
Направления продольных сил (рис. 2.4, б – г) приняты в предположении, что они являются растягивающими (т. е. положительными). Если в результате расчета значение N i получится со знаком «минус», то это будет означать, что в действительности стержень в этом сечении сжат. Поскольку обе части стержня являются равноправными, то N 1 на первом участке в сечении, определяемом координатой z 1, можно определить рассматривая равновесие его правой (рис. 2.4, б) либо левой (рис. 2.4, в) частей. В нашем случае для определения N 1 предпочтительнее рассмотреть равновесие правой части – к ней приложено меньше сил (рис. 2.4, б). Начало координат совмещаем с правым концевым сечением первого участка. Ось zнаправляем налево. Пределы изменения положения сечения вдоль продольной оси 0≤z1≤0,6 м. Спроектируем все силы, действующие на правую часть, на продольную ось. Σ F z=0, N 1 - 24∙z1 = 0, N 1 =24∙z1, N 1(0)= 0, N 1(0,6)= 14,4 кН. Поскольку функция N 1 =24∙z1 получилась линейная, то для построении графика ее изменения вдоль продольной оси (эп. N z) достаточно вычислить значения продольной силы на границах первого участка, отложить их перпендикулярно продольной оси вверх (стержень растянут) и провести через них прямую линию (рис. 2.4, д). Таким образом, в пределах первого участка стержень растянут и нормальная сила изменяется по линейному закону. Этот же результат можно получить, рассматривая равновесие левой части стержня. Здесь при выборе системы координат рассмотрим два варианта. При первом варианте начало координат совмещаем с левым концевым сечением второго участка. Ось z направляем направо. Пределы изменения положения сечения вдоль продольной оси 0,4 м≤ Σ F z=0, N 1 +7,6 – 22 + 24∙( Во втором варианте введем скользящую систему координатных осей. Начало координат совмещаем с левым концевым сечением первого участка. Ось z направляем направо. Пределы изменения положения сечения вдоль продольной оси 0≤ Σ F z=0, N 1 +7,6 – 22 + 24∙ Заметим, что при выборе скользящей системы координат, функция N 1= f (z, q) меняется от нуля, что делает последующие расчеты менее трудоемкими. Сравнивая все три варианта определения N 1, приходим к выводу, что когда мы оставляем ту часть стержня, к которой приложено меньше внешних нагрузок, то расчеты оказываются более простыми. При некотором навыке можно сразу составить выражение для N 1, не изображая отдельные части бруса, на которые он расчленяется поперечными сечениями (рис. 2.4, б, в). Например, при 0≤z1≤0,6 м, N 1 =24∙z1; при 0,4 м≤ при 0≤ Таким образом, на основании метода сечений продольная сила в произвольном поперечном сечении стержня численно равна алгебраической сумме проекций внешних сил, приложенных к стержню по одну сторону от рассматриваемого сечения, на его продольную ось. Причем проекция внешней силы берется со знаком плюс, если сила растягивает часть стержня от точки ее приложения до рассматриваемого сечения и, наоборот, со знаком минус – если сжимает. Осталось определить значение продольной силы N 2 в произвольном сечении, определяемом координатой z 2, на втором участке (рис. 2.4, г). Так как продольная сила N 2 численно равна алгебраической сумме внешних сил, приложенных к стержню слева от сечения (рассматриваем равновесие левой части стержня), то N 2= -7,6 кН (реакция R 1=7,6 кН сжимает часть стержня длиной z 2). Здесь принимаем скользящую систему координат, с началом в левом концевом сечении второго участка. Ось z направляем направо. Эпюра N z на втором участке представлена на рис 2.4, д в виде прямоугольника со знаком минус, поскольку N 2= -7,6 кН =const. Таким образом, в пределах второго участка стержень претерпевает сжатие постоянной нормальной силой. Каждая ордината эп. N z (рис. 2.4, д) в принятом масштабе равна величине продольной силы, действующего в том поперечном сечении стержня, которому соответствует эта ордината. Видно, что на участке между точками приложения сосредоточенных сил R 1 и F продольная сила имеет постоянное значение, а на участке, где приложена распределенная внешняя нагрузка, меняется по линейному закону (рис. 2.4, д). Характерно, что скачки на эп. N z обусловлены наличием в соответствующих сечениях сосредоточенных сил R 1 и F.
ЗАКОН ГУКА Закон пропорциональности удлинения пружины приложенной силе был открыт английским физиком Робертом Гуком (1635-1703г.) Научные интересы Гука были столь широки, что он часто не успевал доводить свои исследования до конца. Это давало повод к острейшим спорам о приоритете в открытии тех или иных законов с крупнейшими учеными (Гюйгенс, Ньютоном и др.). Однако закон Гука был настолько убедительно обоснован многочисленными экспериментами, что тут приоритет Гука никогда не оспаривался. Теория пружины Роберта Гука: Каково растяжение, такова и сила. ДЕФОРМАЦИЯ Деформация - изменение объема или формы тела.
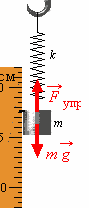
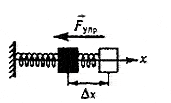
В качестве примера рассмотрим деформацию (растяжение или сжатие) упругой пружины. Под действием приложенной к пружине силы, равной весу подвешенного груза, пружина деформируется (т.е. ее длина увеличится на величину "х"). Возникает сила, противодействующая деформации -сила упругости. Сила упругости приложена к телу, вызывающему деформацию (к грузу). Сила упругости растянутой пружины уравновешивает силу тяжести, действующую на груз.
Сила упругости возникает только при деформации тела. При исчезновении деформации тела исчезает и сила упругости.
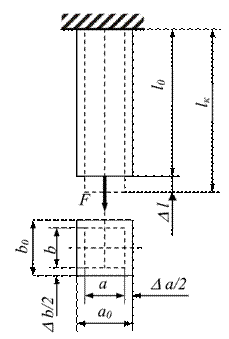
ЗАКОН ГУКА Сила упругости прямо пропорциональна величине деформации.Закон Гука справедлив при малых (упругих) деформациях тел. Модуль силы Гука: F упр = k | x | где k -коэффициент упругости или жесткость пружины (ед.изм. в СИ - 1 Н/м) х - удлинение пружины или величина деформации пружины (ед.изм. в СИ - 1м) Fупр - сила упругости (ед.изм. в СИ - 1Н) Деформации и перемещения. Величина, на которую изменится длина бруса (или одного из его участков) под действием продольных сил, называется продольной деформацией (рис. 6). Относительная продольная деформация – отношение абсолютной продольной деформации Dl к первоначальной длине стержня l: ε = Dl/l0 Величина Δа (Δb), на которую изменится размерпоперечного сечениябруса а (b) под действием продольной силы, называется поперечной деформацией. Отношение абсолютной поперечной деформации, Dа (Db) к первоначальному размеру сечения бруса а (b), называется относительной поперечной деформацией:
Рис. 6. Схема деформирования стержня Статический момент площади Полярный момент инерции Полярным моментом инерции плоской фигуры относительно полюса (точки), лежащего в той же плоскости, называется сумма произведений элементарных площадок этой фигуры на квадрат их расстояний до полюса. Iρ= Σ ρ2dA. Единица измерений полярного момента инерции - м4, из чего следует, что он не может быть отрицательным.
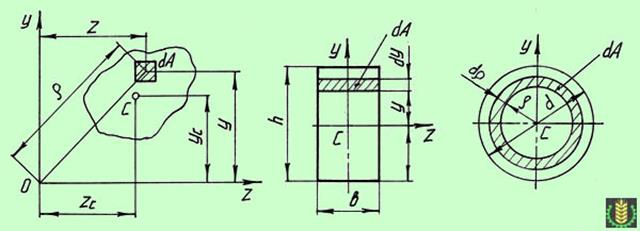
Очевидно, что полярный момент инерции кольцевого сечения равен разности полярных моментов инерции большого и малого кругов, ограничивающих это сечение. *** Осевой момент инерции Осевым моментом инерции плоской фигуры относительно оси, лежащей в той же плоскости, называется взятая по всей площади сумма произведений площадей элементарных площадок на квадрат расстояний от них до этой оси (рис).
Осевой момент инерции обозначается I с индексом, соответствующим оси: Ix= Σ y2dA; Iy= Σ x2dA. Если при этом площадь элементарных площадок принять стремящимися к минимуму, то можно использовать методы интегрального исчисления, заменив знак суммы Σ на знак интеграла ∫. Ix+ Iy= Iρ. Так как интеграл суммы равен сумме интегралов, то момент инерции сложной фигуры можно вычислить как сумму моментов инерции простых фигур, на которые разбивают сложную фигуру. Приведем формулы для определения осевых моментов инерции наиболее часто встречающихся при расчетах форм сечений:
***
Центробежный момент инерции Центробежным моментом инерции плоской фигуры называют взятую по всей площади сумму произведений элементарных площадок на расстояние до двух взаимно перпендикулярных осей: Ixy= Σ xy dA, где x, y - расстояния от площадки dA до осей x и y. Центробежный момент инерции входит в формулы для определения положения главных осей несимметричных сечений. ix= √ (Ix/ A), iy= √ (Iy/ A), (здесь и далее знак "√" - знак корня) где Ix, Iy - осевые моменты инерции сечения относительно центральных осей; А - площадь сечения. Деформация кручения Основные понятия о кручении. Кручение круглого бруса. Кручением называют такой вид деформации, при котором в любом поперечном сечении бруса возникает только крутящий момент, т. е. силовой фактор, вызывающий круговое перемещение сечения относительно оси, перпендикулярной этому сечению, либо препятствующий такому перемещению. Другими словами - деформации кручения возникают, если к прямому брусу в плоскостях, перпендикулярных его оси приложить пару или пары сил. В машинах и механизмах кручению наиболее часто подвергаются круглые или трубчатые валы, поэтому расчеты на прочность и жесткость чаще всего производят для таких узлов и деталей. Рассмотрим кручение круглого цилиндрического вала.
Из этого можно заключить, что при кручении круглого цилиндрического бруса (вала) справедлива гипотеза плоских сечений, а также предположить, что радиусы окружностей остаются при деформации прямыми (поскольку их диаметры не изменились). А поскольку в сечениях вала отсутствуют продольные силы, то расстояние между ними сохраняется. Следовательно, деформация кручения круглого вала заключается в повороте поперечных сечений относительно друг друга вокруг оси кручения, причем углы поворота их прямо пропорциональны расстояниям от закрепленного сечения - чем дальше от закрепленного конца вала находится какое-либо сечение, тем на больший угол относительно оси вала оно закручивается.
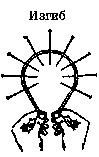
Угол (рис. 1) поворота свободного конца вала (концевого сечения) называется полным углом закручивания цилиндрического бруса (вала). Если мы рассмотрим тонкий слой на поверхности вышеупомянутого резинового цилиндрического бруса (рис. 1), ограниченный ячейкой сетки cdef, то заметим, что эта ячейка при деформации перекашивается, и ее сторона, удаленная от закрепленного сечения, смещается в сторону закручивания бруса, занимая положение cde1f1. Следует отметить, что аналогичная картина наблюдается при деформации сдвига, только в этом случае поверхность деформируется из-за поступательного перемещения сечений друг относительно друга, а не из-за вращательного перемещения, как при деформации кручения. На основании этого можно сделать вывод, что при кручении в поперечных сечениях возникают только касательные внутренние силы (напряжения), образующие крутящий момент. Итак, крутящий момент есть результирующий момент относительно оси бруса внутренних касательных сил, действующих в поперечном сечении.
Напряжения при изгибе Деформация кручения Пример решения задачи на кручение Определить минимальный допустимый диаметр вала d, передающего крутящий момент Мкр = 464 Нм, если допускаемое напряжение кручения [τкр] = 30 МПа. Решение По известному передаваемому крутящему моменту можно определить момент сопротивления кручению: Wr= Мкр/ [τкр] = 464 / 30 х 106= 15,6 х 10-6м3. Из зависимости между моментом сопротивления кручению и диаметром вала Wr≈ 0,2D3 находим минимальный допустимый диаметр: D ≈3√ Wr/ 0,02≈ 43 мм (здесь и далее √ - знак корня). Округляя найденное значение диаметра до стандартной величины (в большую сторону), принимаем D = 45 мм. ***
Пример построения эпюры крутящих моментов Силовая передача (трансмиссия), изображенная на рис. 2 состоит из вала, на котором размещены три шестерни - одна ведущая (А) и две ведомые (В и С). Решение Очевидно, что свободные концы вала, (вращающиеся в подшипниках) не подвержены действию вращающих моментов, т. е. крутящие моменты на участках 1 и 4 равны нулю. К шестерне В приложен вращающий момент 120 Нм, который направлен в противоположную сторону от ведущего скручивающего момента, приложенного к шестерне А. Следовательно крутящий момент на участке 3 будет равен разности крутящих моментов, приложенных к шестерням А и В. На эпюре это отобразится в виде ступени величиной 120 Нм, расположенной напротив сечения, где размещена шестерня В. К шестерне С приложен вращающий момент 180 Нм, направление которого противоположно моменту, приложенному к ведущей шестерне А, поэтому, начиная с сечения под шестерней С, крутящий момент будет равен разнице между скручивающим моментом шестерни А и моментами, приложенными к шестерням В и С, т. е.
Построив эпюру крутящих моментов, действующих в сечениях вала данной силовой передачи как показано на рис. 2, отмечаем, что максимальной величины - 300 Нм крутящий момент достигает на участке 2, т. е. этот участок и является критическим (наименее надежным). Теперь попробуем изменить расположение шестерен на валу, разместив ведущую шестерню А между ведомыми шестернями В и С, как показано на рис. 3. Приложенные к шестерням вращающие моменты оставим без изменения и построим эпюру крутящих моментов для измененной конструкции (рис. 3). Из полученной эпюры видно, что на участке 2 (между шестернями В и А) крутящий момент равен - 120 Нм, на участке 3 — + 180 Нм, а на участках 1 и 4 крутящие моменты равны нулю, как и в предыдущей конструкции. И если в рассмотренной ранее конструкции максимальны
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 647; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.38.67 (0.011 с.) |





 , как и равнодействующая внутренних сил, приложенных на элементарной площадке, является векторной величиной и может быть разложено на две составляющие: перпендикулярное к рассматриваемой площадке – нормальное напряжение σn и касательное к площадке – касательное напряжение
, как и равнодействующая внутренних сил, приложенных на элементарной площадке, является векторной величиной и может быть разложено на две составляющие: перпендикулярное к рассматриваемой площадке – нормальное напряжение σn и касательное к площадке – касательное напряжение  n. Здесь n – нормаль к выделенной площадке.
n. Здесь n – нормаль к выделенной площадке.

 При анализе напряжений в окрестности рассматриваемой точки выделяется бесконечно малый объемный элемент (параллелепипед со сторонами dx, dy, dz), по каждой грани которого действуют, в общем случае, три напряжения, например, для грани, перпендикулярной оси x (площадка x) – σ x
При анализе напряжений в окрестности рассматриваемой точки выделяется бесконечно малый объемный элемент (параллелепипед со сторонами dx, dy, dz), по каждой грани которого действуют, в общем случае, три напряжения, например, для грани, перпендикулярной оси x (площадка x) – σ x 

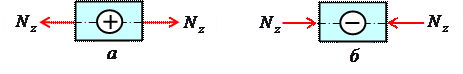
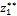 ≤1,0 м. Спроектируем все силы, действующие на левую часть, на продольную ось.
≤1,0 м. Спроектируем все силы, действующие на левую часть, на продольную ось.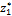 ≤0,6 м. Имеем
≤0,6 м. Имеем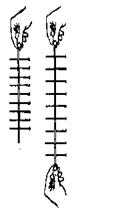



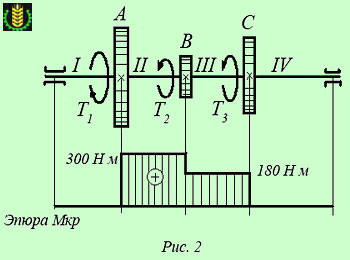 К шестерням приложены вращающие моменты: РА= 300 Нм, РВ= 120 Нм, РС= 180 Нм.
К шестерням приложены вращающие моменты: РА= 300 Нм, РВ= 120 Нм, РС= 180 Нм. 



