Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Растяжение и сжатие. Деформации. Закон Гука.Содержание книги
Похожие статьи вашей тематики
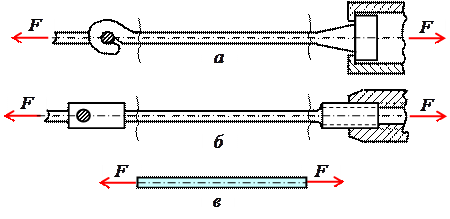
Поиск на нашем сайте Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы N, а прочие силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю. Это самый простой и часто встречающийся вид деформации. Обычно он наблюдается когда внешняя нагрузка действует вдоль продольной оси стержня. Продольной осью стержня называется линия, проходящая через центры тяжести поперечных сечений. Обычным является растяжение стержня силами, приложенными к его концам. Передача усилий к стержню может быть осуществлена различными способами, как это показано на рис. 2.1.
Рис. 2.1
Во всех случаях, однако, система внешних сил образует равнодействующую F, направленную вдоль оси стержня. Поэтому независимо от условий крепления растянутого стержня, расчетная схема в рассматриваемых случаях (рис. 2.1, а, б) оказывается единой (рис. 2.1, в) согласно принципу Сен – Венана. Если воспользоваться методом сечений (рис. 2.2), то становится очевидным, что во всех поперечных сечениях стержня возникают нормальные силы N z, равные силе F (рис. 2.2, б). Сжатие отличается от растяжения, формально говоря, только знаком силы N z. При растяжении нормальная сила N z направлена от сечения (рис. 2.2, б), а при сжатии – к сечению.
Рис. 2.2
Растягивающие продольные силы принято считать положительными ( рис. 2.3, а), а сжимающие – отрицательными (рис. 2.3, б).
Рис. 2.3
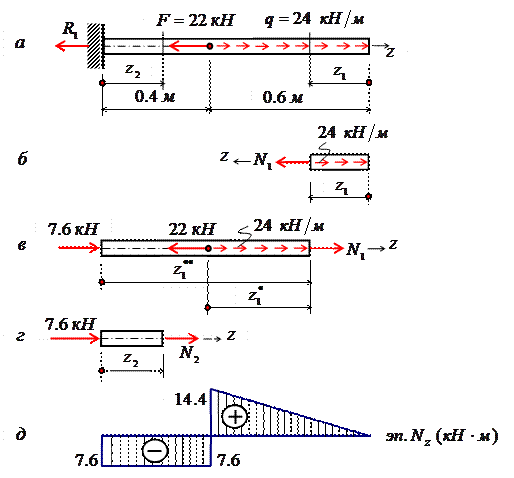
Вместе с тем между растяжением и сжатием могут обнаружиться и качественные различия, как, например, при изучении процессов разрушения материала или при исследовании поведения длинных и тонких стерж-ней, для которых сжатие сопровождается, как правило, изгибом. При расчете стержней, испытывающий деформацию растяжения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от N z), возникающих в стержне, и нахождение линейных перемещений в зависимости от внешней нагрузки. Продольные силы (N z), возникающие в поперечных сечениях стержня, определяются по внешней нагрузке с помощью метода сечений. График, показывающий изменение продольных сил по длине оси стержня, называется эпюрой продольных сил (эп. N z). Он дает наглядное представление о законе изменения продольной силы. Осью абсцисс служит ось стержня. Каждая ордината графика – продольная сила (в масштабе сил) в данном сечении стержня. Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти N max при растяжении-сжатии). Сечение, где действует максимальное усилие будем называть опасным. Перед построением эпюр необходимо освободить брус, в котором будем строить эпюры от опорных связей (выделить объект равновесия) и приложить к нему все действующие внешние силы (активные и реактивные). Затем необходимо установить границы участков, в пределах которых закон изменения внутренних сил постоянный. Границами таких участков являются сечения, где приложены сосредоточенные силы или начинается и кончается распределенная нагрузка, а также сечения, где имеется перелом стержня. Применяя метод сечений и учитывая правила знаков изложенные выше, получаем уравнения изменения внутренних сил в пределах длины каждого участка бруса. Затем, используя, полученные зависимости строим графики (эпюры) этих усилий. Ординаты эпюр в определенном масштабе откладываем от базисной линии, которую проводим параллельно оси бруса. Рассмотрим стержень постоянного поперечного сечения, жестко защемленный правым концевым сечением и нагруженный заданной внешней сосредоточенной нагрузкой F и распределенной q (рис. 2.4, а). Прежде всего определим опорную реакцию R 1, задавшись ее направлением вдоль оси z. Σ F z=0, - R 1 - 22 + 24∙0,6 = 0, R 1= -7,6 кН. Знак минус говорит о том, что действительное направление опорной реакции R 1 противоположно показанному на рис. 2.4, а. Исправляем его и в дальнейших расчетах знак минус у опорной реакции R 1 не учитываем (рис. 2.4, в, г). Под участком будем понимать часть стержня, на которой N z представляется некоторым аналитическим выражением. На другом участке N z будет определяться другой функцией. Границами участка являются начало и конец стержня, сечения, где приложены сосредоточенные нагрузки, начинается и заканчивается распределенная нагрузка. В нашем случае стержень разбивается на два участка. В пределах первого участка мысленно рассечем стержень на две части нормальным сечением (рис. 2.4, б, в).
Рис. 2.4
Направления продольных сил (рис. 2.4, б – г) приняты в предположении, что они являются растягивающими (т. е. положительными). Если в результате расчета значение N i получится со знаком «минус», то это будет означать, что в действительности стержень в этом сечении сжат. Поскольку обе части стержня являются равноправными, то N 1 на первом участке в сечении, определяемом координатой z 1, можно определить рассматривая равновесие его правой (рис. 2.4, б) либо левой (рис. 2.4, в) частей. В нашем случае для определения N 1 предпочтительнее рассмотреть равновесие правой части – к ней приложено меньше сил (рис. 2.4, б). Начало координат совмещаем с правым концевым сечением первого участка. Ось zнаправляем налево. Пределы изменения положения сечения вдоль продольной оси 0≤z1≤0,6 м. Спроектируем все силы, действующие на правую часть, на продольную ось. Σ F z=0, N 1 - 24∙z1 = 0, N 1 =24∙z1, N 1(0)= 0, N 1(0,6)= 14,4 кН. Поскольку функция N 1 =24∙z1 получилась линейная, то для построении графика ее изменения вдоль продольной оси (эп. N z) достаточно вычислить значения продольной силы на границах первого участка, отложить их перпендикулярно продольной оси вверх (стержень растянут) и провести через них прямую линию (рис. 2.4, д). Таким образом, в пределах первого участка стержень растянут и нормальная сила изменяется по линейному закону. Этот же результат можно получить, рассматривая равновесие левой части стержня. Здесь при выборе системы координат рассмотрим два варианта. При первом варианте начало координат совмещаем с левым концевым сечением второго участка. Ось z направляем направо. Пределы изменения положения сечения вдоль продольной оси 0,4 м≤ Σ F z=0, N 1 +7,6 – 22 + 24∙( Во втором варианте введем скользящую систему координатных осей. Начало координат совмещаем с левым концевым сечением первого участка. Ось z направляем направо. Пределы изменения положения сечения вдоль продольной оси 0≤ Σ F z=0, N 1 +7,6 – 22 + 24∙ Заметим, что при выборе скользящей системы координат, функция N 1= f (z, q) меняется от нуля, что делает последующие расчеты менее трудоемкими. Сравнивая все три варианта определения N 1, приходим к выводу, что когда мы оставляем ту часть стержня, к которой приложено меньше внешних нагрузок, то расчеты оказываются более простыми. При некотором навыке можно сразу составить выражение для N 1, не изображая отдельные части бруса, на которые он расчленяется поперечными сечениями (рис. 2.4, б, в). Например, при 0≤z1≤0,6 м, N 1 =24∙z1; при 0,4 м≤ при 0≤ Таким образом, на основании метода сечений продольная сила в произвольном поперечном сечении стержня численно равна алгебраической сумме проекций внешних сил, приложенных к стержню по одну сторону от рассматриваемого сечения, на его продольную ось. Причем проекция внешней силы берется со знаком плюс, если сила растягивает часть стержня от точки ее приложения до рассматриваемого сечения и, наоборот, со знаком минус – если сжимает. Осталось определить значение продольной силы N 2 в произвольном сечении, определяемом координатой z 2, на втором участке (рис. 2.4, г). Так как продольная сила N 2 численно равна алгебраической сумме внешних сил, приложенных к стержню слева от сечения (рассматриваем равновесие левой части стержня), то N 2= -7,6 кН (реакция R 1=7,6 кН сжимает часть стержня длиной z 2). Здесь принимаем скользящую систему координат, с началом в левом концевом сечении второго участка. Ось z направляем направо. Эпюра N z на втором участке представлена на рис 2.4, д в виде прямоугольника со знаком минус, поскольку N 2= -7,6 кН =const. Таким образом, в пределах второго участка стержень претерпевает сжатие постоянной нормальной силой. Каждая ордината эп. N z (рис. 2.4, д) в принятом масштабе равна величине продольной силы, действующего в том поперечном сечении стержня, которому соответствует эта ордината. Видно, что на участке между точками приложения сосредоточенных сил R 1 и F продольная сила имеет постоянное значение, а на участке, где приложена распределенная внешняя нагрузка, меняется по линейному закону (рис. 2.4, д). Характерно, что скачки на эп. N z обусловлены наличием в соответствующих сечениях сосредоточенных сил R 1 и F.
ЗАКОН ГУКА Закон пропорциональности удлинения пружины приложенной силе был открыт английским физиком Робертом Гуком (1635-1703г.) Научные интересы Гука были столь широки, что он часто не успевал доводить свои исследования до конца. Это давало повод к острейшим спорам о приоритете в открытии тех или иных законов с крупнейшими учеными (Гюйгенс, Ньютоном и др.). Однако закон Гука был настолько убедительно обоснован многочисленными экспериментами, что тут приоритет Гука никогда не оспаривался. Теория пружины Роберта Гука: Каково растяжение, такова и сила. ДЕФОРМАЦИЯ Деформация - изменение объема или формы тела.
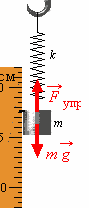
В качестве примера рассмотрим деформацию (растяжение или сжатие) упругой пружины. Под действием приложенной к пружине силы, равной весу подвешенного груза, пружина деформируется (т.е. ее длина увеличится на величину "х"). Возникает сила, противодействующая деформации -сила упругости. Сила упругости приложена к телу, вызывающему деформацию (к грузу). Сила упругости растянутой пружины уравновешивает силу тяжести, действующую на груз.
Сила упругости возникает только при деформации тела. При исчезновении деформации тела исчезает и сила упругости.
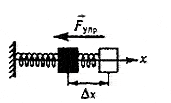
ЗАКОН ГУКА Сила упругости прямо пропорциональна величине деформации.Закон Гука справедлив при малых (упругих) деформациях тел. Модуль силы Гука: F упр = k | x | где k -коэффициент упругости или жесткость пружины (ед.изм. в СИ - 1 Н/м) х - удлинение пружины или величина деформации пружины (ед.изм. в СИ - 1м) Fупр - сила упругости (ед.изм. в СИ - 1Н)
|
||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1219; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.008 с.) |


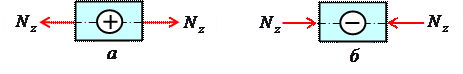
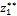 ≤1,0 м. Спроектируем все силы, действующие на левую часть, на продольную ось.
≤1,0 м. Спроектируем все силы, действующие на левую часть, на продольную ось.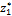 ≤0,6 м. Имеем
≤0,6 м. Имеем