
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Растяжение стального образца с измерением упругих деформацийСодержание книги
Поиск на нашем сайте
Цель работы: Экспериментальная проверка закона Гука при растяжении. Определение модуля Юнга и коэффициента Пуассона стали.
Общие сведения
образец в пределах упругих деформаций. На образце (рис. 1) установлены два продольных и два поперечных тензометра. Для измерения деформаций образца в работе используется электротензометрический метод, изложенный в главе 3. 1. Проверка закона Гука
 Опытная проверка закона Гука при растяжении производится на основе экспериментально определенной диаграммы растяжения (рис.2), которая строится по результатам испытаний. Опытная проверка закона Гука при растяжении производится на основе экспериментально определенной диаграммы растяжения (рис.2), которая строится по результатам испытаний.
Справедливость закона Гука устанавливается наличием на диаграмме прямолинейного участка. 2. Определение модуля Юнга материала Модуль Юнга материала определяется по формуле закона Гука
где Δ Р – ступень нагрузки, l – база тензометра продольной деформации, А – площадь поперечного сечения образца, Δ l – абсолютное удлинение образца на отрезке длиной l. Зная среднее приращение отсчетов Δ n 1cp электротензометра продольной деформации (из таблицы наблюдений) и цену деления прибора в относительной деформации на одно деление K e, можно вычислить относительную продольную деформацию образца
Цена деления прибора – электротензометра устанавливается опытным путем (см. главу 3). Подставляя в формулу (1) данные опыта (2), получим
3. Определение коэффициента Пуассона Коэффициентом Пуассона или коэффициентом поперечной деформации называется отношение относительной поперечной деформации к относительной продольной деформации, взятое по модулю
где m – коэффициент Пуассона, e – относительная продольная деформация, e¢ – относительная поперечная деформация. Относительная поперечная деформация образца вычисляется по формуле
где Δ n 2cp – среднее приращение отсчетов электротензометра поперечной деформации (берется из таблицы наблюдений), K e¢ – цена деления электротензометра поперечной деформации. Если характеристики (база, цена деления) тензометров продольной и поперечной деформации одинаковы, то величина коэффициента Пуассона определяется по формуле
Испытательная машина ГЗИП
Работа выполняется на испытательной машине ГЗИП (рис. 3), предельная нагружающая способность которой может быть 2 т (20 кН) и 5 т (50 кН). Образец 1 закрепляют в захваты 2 и 3. Нижний захват перемещается с помощью винта 4. Перемещение винта осуществляется рукояткой 5. Нагрузка измеряется силоизмерителем 6.
Порядок выполнения работы
1. Замерить размеры поперечного сечения образца b и h. 2. Установить образец в захваты машины. 3. Нагрузить образец начальной нагрузкой P 0 (для обжатия образца в захватах машины). 4. Произвести начальные отсчеты по продольным и поперечным тензометрам. 5. Плавно увеличивать нагрузку одинаковыми ступенями до напряжения в образце, равного (0,80¸0,90) sпц . Одновременно на каждой стадии нагружения делать отсчеты по тензометрам. 6. По окончании опыта разгрузить образец до нагрузки P 0 и снять контрольные отсчеты по тензометрам, которые должны совпадать с первоначальными. 7. Выполнить отчет по прилагаемой форме.
ОТЧЕТ 4
Цель работы:………………………………………..………………………….. …………………………………………………………….……………………… …………………………………………………………….……………………… Испытательная машина………………………………………………………… Измерительные приборы……………………………………………………….. Тензометры: тип……….………..; марка……..……….; база l = ………..….мм. Цена деления рычажного тензометра n = ………… Цена деления электротензометра K e = …………....
Результаты наблюдений
Модуль Юнга
Коэффициент Пуассона
Выводы по работе ………………………………………………..……….. ……………………………………………………………………………………… Отчет принял …………………….
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 304; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.98.186 (0.009 с.) |



 В работе подвергается испытанию на растяжение плоский стальной
В работе подвергается испытанию на растяжение плоский стальной









 Схема образца с тензометром
Схема образца с тензометром


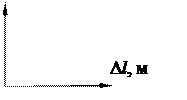
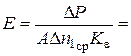 …………………….=………….МПа.
…………………….=………….МПа.



