
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение реакции средней опоры двухпролетной неразрезной балкиСодержание книги
Поиск на нашем сайте
Цель работы: Экспериментальное определение реакции средней опоры неразрезной балки и сравнение её с результатом теоретического расчета.
Общие сведения
Расчетная схема двухпролетной неразрезной балки с двумя консолями представлена на рис.1.
Теоретическое значение реакции средней опоры для балки, определенное, например, на основе метода сил или других методов, показанной на рис. 1, равно
где l – пролет между опорами D и В, В и С; a – длина консольных участков балки. Для определения реакции опытным путем рассматривается балка на двух опорах пролетом 2 l (рис. 2, а).
Нагрузим балку на концах консолей сосредоточенными силами Р. Под действием указанных сил балка изогнется и сечение В при этом переместится вверх (рис. 2, а). Опытное значение величины реакции
Порядок выполнения работы
1.Установить балку на две опоры, замерить расстояние 2 l между опорами D и С и длины консолей a. 2. Записать показания индикатора, находящегося в сечении В в ненагруженном состоянии балки (можно показания индикатора установить на ноль). 3. На консоли плавно подвесить грузы Р. 4. Записать новое показание индикатора. 5. Плавно нагрузить подвеску, прикрепленную в точке В. Нагружение производить до тех пор, пока стрелка индикатора не вернется в первоначальное положение, соответствующее ненагруженному состоянию балки. 6. Подсчитать вес груза Q, находящегося на подвеске. Это и будет величина реакции средней опоры 7. Определить процент расхождения между теоретическим и экспериментальным значениями реакции
8. Оформить отчет по прилагаемой форме.
ОТЧЕТ 13 Цель работы: …………………………………………………………………… …………….………………………………………………………………………. Схема установки
Размер балки: пролет 2 l =……… см; длина консоли a = …… см. Результаты опыта: нагрузка Р = …………… Н. Вес груза в пролете (величина реакции средней опоры Q = …………… Н. Реакция средней опоры, вычисленная аналитически:
Процент расхождения между теоретическим и опытным значениями реакции:
Выводы по работе ………………………………………………………….. ……………………………………………………………………………………… Отчет принял …………………….. ОПРЕДЕЛЕНИЕ КРИТИЧЕСКОЙ СИЛЫ СЖАТОГО СТЕРЖНЯ
Цель работы: Исследование явления потери устойчивости прямолинейной формы равновесия при осевом сжатии стержня. Опытная проверка формулы Эйлера для определения критической силы.
Общие сведения
При сравнительно малой величине силы, меньшей некоторого критического значения P < P кр, стержень будет сохранять прямолинейную форму равновесия. Если отклонить стержень в сторону, например, путем приложения кратковременно действующей горизонтальной силы, он будет после ряда колебаний возвращаться к первоначальной прямолинейной форме, как только будет удалена добавочная сила, вызвавшая отклонение. Такая форма равновесия стержня называется устойчивой. При значении сжимающей силы, равном критическому значению P=P кр, стержень будет находиться в состоянии безразличного равновесия. Будучи незначительно отклоненным от первоначального прямолинейного положения и предоставленным самому себе, он остается в равновесии и в отклоненном состоянии (рис. 1, б). И, наконец, если сила P станет больше критической P > P кр, то прямолинейная форма равновесия стержня будет неустойчивой. При силе большей критической стержень получит новую криволинейную форму равновесия (рис. 1, в) или разрушится. В практических расчетах критическую силу рассматривают как опасную (предельную) нагрузку. Наименьшее значение центрально приложенной сжимающей силы P, при котором прямолинейная форма равновесия стержня становится неустойчивой, называется критической силой. Величина критической силы определяется по формуле Эйлера
где E – модуль Юнга материала стержня; I min – минимальный осевой момент инерции поперечного сечения стержня; m – коэффициент приведения длины, который зависит от способа закрепления концов стержня; l – длина стержня. Для четырех наиболее часто встречающихся случаев закрепления концов стержня коэффициент m имеет следующие значения: · для стержня с шарнирно закрепленными концами m = 1; · для стержня с одним заделанным и другим шарнирно закрепленным концом m = 0,7; · для стержня с заделанными концами m = 0,5; · для стержня с одним заделанным и другим свободным концом m = 2. Критическое напряжение в стержне определяется по формуле
где
А – площадь поперечного сечения стержня. Формула Эйлера применима лишь в том случае, если потеря устойчивости стержня происходит при напряжении, меньшем предела пропорциональности
где sпц – предел пропорциональности материала. Условие применимости формулы Эйлера может быть выражено в зависимости от гибкости стержня. Формула Эйлера применима, если гибкость стержня l равна или больше предельного ее значения lпред, то есть
где Установлено, что формула Эйлера применима при гибкостях, превышающих: для чугуна – 80; для дерева – 110; для стали марки Ст.3 – 100. При значениях гибкостей l, меньших предельных значений, формула Эйлера не применима, так как потеря устойчивости происходит при напряжениях, превосходящих предел пропорциональности. В этих случаях критические напряжения определяются по эмпирической формуле Ясинского, которая для стали и дерева записывается так:
где a, b – коэффициенты, зависящие от материала. Для стали Ст. 3 при гибкостях l = 40 Для сосны при гибкостях l = 40 Для стержней с малой гибкостью (l = 0
Испытательная машина
Испытания стержней на устойчивость проводятся на испытательной машине ГЗИП, предельная нагружающая способность которой может быть 20 или 50 кН. Возможно применение любой другой испытательной машины вертикального типа, предназначенной для статических испытаний на сжатие достаточно длинных стержней или специально изготовленной установки. К захватам машины прикрепляются специальные зажимы для закрепления концов плоского стержня. На рис. 2 показано устройство таких зажимов. При отвинченных винтах концы образца могут свободно поворачиваться, опираясь на зажимы своими острыми ребрами, это соответствует случаю шарнирного закрепления (m = 1); длина стержня измеряется от его концов. При завинченных винтах концы стержня не могут поворачиваться, что соответствует случаю жесткого закрепления обоих концов стержня (m = 0,5). В этом случае длина стержня измеряется между осями винтов, как показано на рис. 2. Если жестко закреплен только один конец стержня, а другой может свободно поворачиваться (m = 0,7), то длина стержня измеряется от незакрепленного конца до оси завинченного винта.
Порядок выполнения работы 1. Замерить размеры поперечного сечения и длину стержня. 2. Установить стержень в зажимах испытательной машины. В отчете записать характер закрепления верхнего и нижнего конца стержня. 3. Вычислить гибкость стержня по формуле
4. Медленно и ступенями нагружать стержень вручную. Во время нагружения наблюдать за величиной нагрузки и поведением стержня. При испытании на машине нагрузка вначале плавно возрастает, затем при достижении определенной величины нагрузки стержень начнет изгибаться и рост нагрузки прекратится. Это значение нагрузки является критическим и записывается в отчете. 5. Вычислить величину критической силы. При этом, если величина гибкости стержня равна или выше предельного ее значения ( 6. Сравнить величину критической силы, полученную опытным путем, с вычисленной по формуле Эйлера. Определить процент расхождения. 7. Результаты испытания представить по прилагаемой форме.
ОТЧЕТ 14
Цель работы:…………………………………………….……………………… …………………………………………………………………………………….. ……………………………………………………………………………………..
Испытательная машина………………………………………………………….. Схема нагружения показана на рисунке.
Размеры образца: b =……………….см; h =……………….см; l = ……………….см. Модуль Юнга материала E = 200 ГПа. Коэффициент приведенной длины m =………………. Площадь поперечного сечения А = b h = ……………..см2. Наименьший момент инерции сечения
Наименьший радиус инерции
Гибкость стержня
Выполнение условия применимости формулы Эйлера (Ясинского) ( Величина критической силы по формуле Эйлера (Ясинского)
Величина критической силы, полученная из опыта
Расхождение в процентах между теоретическим и опытным значениями критической силы
Выводы по работе ……………………………………………………….. …………………………………………………………………………………… ……………………………………………………………………………………. ……………………………………………………………………………………. ……………………………………………………………………………………. ……………………………………………………………………………………. Отчет принял ……………………………..
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 489; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.006 с.) |




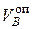 определим из условия равенства нулю перемещения балки в точке В. Для этого в сечении В проложим силу Q такую, чтобы сечение В вернуть в исходное положение (рис. 2, б). Тогда искомая величина реакции будет равна этой силе Q, то есть
определим из условия равенства нулю перемещения балки в точке В. Для этого в сечении В проложим силу Q такую, чтобы сечение В вернуть в исходное положение (рис. 2, б). Тогда искомая величина реакции будет равна этой силе Q, то есть 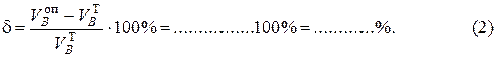
 =……………=……………Н.
=……………=……………Н.
 Рассмотрим достаточно длинный по сравнению с его поперечными размерами стержень, шарнирно опертый по концам и нагруженный осевой силы P (рис. 1, а).
Рассмотрим достаточно длинный по сравнению с его поперечными размерами стержень, шарнирно опертый по концам и нагруженный осевой силы P (рис. 1, а).

 – гибкость стержня;
– гибкость стержня; – минимальный радиус инерции сечения стержня;
– минимальный радиус инерции сечения стержня;

 – предельная гибкость стержня.
– предельная гибкость стержня.
 100 величина a = 310 МПа, b = 1,14 МПа.
100 величина a = 310 МПа, b = 1,14 МПа.
 .
. ), то величина критической силы определяется по формуле Эйлера (1), если ниже (
), то величина критической силы определяется по формуле Эйлера (1), если ниже ( ), то
), то 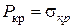 А, где
А, где  определяется по формуле Ясинского (5).
определяется по формуле Ясинского (5). Материал: сталь Ст. 3
Материал: сталь Ст. 3 = ………………..=………………………см4.
= ………………..=………………………см4.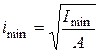 =…………………=………………………см.
=…………………=………………………см. или
или  )…………………………………………
)………………………………………… =………………….=………………Н.
=………………….=………………Н. …………………..Н.
…………………..Н. = …………………=……………..%.
= …………………=……………..%.


