
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Деформации при растяжении (сжатии)
Деформации при растяжении (сжатии) Oпыты показывают, что при растяжении длина стержня увеличивается, а поперечные размеры уменьшаются, при сжатии - наоборот (рис.2.7).
Относительная продольная деформация e и относительная поперечная деформация e ' равны В пределах малых удлинений для большинства материалов справедлив закон Гука - нормальные напряжения в поперечном сечении прямо пропорциональны относительной линейной деформации e Так как Эта зависимость также выражает закон Гука. Сформулировать условие жесткости при изгибе. Условие прочности при изгибе Максимальное нормальное напряжение в балке возникает в сечении, где изгибающий момент достигает наибольшей по модулю величины, то есть в опасном сечении Условие прочности при изгибе формулируется следующим образом: Балка будет прочной, если максимальные нормальные напряжения не превысят допускаемых напряжений Величина допускаемых напряжений назначается в зависимости от материала, из которого изготовлена балка. Пластичные материалы обладают примерно равными пределами текучести на сжатие Для хрупких материалов, у которых прочность при сжатии выше, чем при растяжении, допускаемые напряжения на растяжение и сжатие, как правило, не равны между собой где Что понимается под пределом прочности материала. «Временное сопротивление разрушению», то есть напряжение, соответствующее наибольшему усилию, предшествующему разрыву образца при (статических) механических испытаниях. Термин происходит от того представления, что материал может бесконечно долго выдержать любую статическую нагрузку, если она создаёт напряжения меньшие по величине, чем временное сопротивление. При нагрузке, соответствующей временному сопротивлению (или даже превышающей её — в реальных и квазистатических испытаниях) разрушение материала (разделение образца на несколько частей) произойдёт через какой-то конечный промежуток времени, возможно, что и практически сразу. Что понимается под гибкостью стержня и от чего она зависит. Гибкость стержня — отношение расчетной длины стержня
Это выражение играет важную роль при проверке сжатых стержней на устойчивость. В частности, от гибкости зависит коэффициент продольного изгиба Расчетная длина
45. Привести примеры различного вида механизмов. - Кривошип – звено, совершающее полный оборот вокруг неподвижной оси. - Коромысло – звено, совершающее неполный оборот вокруг неподвижной оси; - Ползун – звено, образующее поступательную пару со стойкой. - Шатун- звено, не образующее кинематической пары со стойкой и совершающее плоское движение. - Кулиса – звено с пазом, по которому перемещается ползун. Кулиса может быть качающейся, вращающейся, движущейся поступательно. - Кривошипный-ползунный механизм; - Шарнирный четырех звенный механизм; - Кулисный механизм; - Двухползунный рычажный механизм; - Кулисный кривошипноползунный механизм; - Кулисный коромыслово-ползунный механизм; - Простой зубчатый механизм; - Планетарный механизм; - Фрикционный механизм; Деформации при растяжении (сжатии) Oпыты показывают, что при растяжении длина стержня увеличивается, а поперечные размеры уменьшаются, при сжатии - наоборот (рис.2.7).
Относительная продольная деформация e и относительная поперечная деформация e ' равны В пределах малых удлинений для большинства материалов справедлив закон Гука - нормальные напряжения в поперечном сечении прямо пропорциональны относительной линейной деформации e Так как Эта зависимость также выражает закон Гука.
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 494; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.156.13 (0.01 с.) |

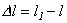 ;
;  .
. ;
;  .
. .
. , то подставляя в закон Гука (2.2) можно получить формулу для определения абсолютного удлинения (укорочения) стержня
, то подставляя в закон Гука (2.2) можно получить формулу для определения абсолютного удлинения (укорочения) стержня .
. .
. .
. и на растяжение
и на растяжение  равны между собой и поэтому
равны между собой и поэтому  .
. и, поэтому, необходимо записывать два условия прочности
и, поэтому, необходимо записывать два условия прочности ,
,  ,
, и
и  - расстояния от нейтральной оси до наиболее удаленных растянутого и сжатого волокон.
- расстояния от нейтральной оси до наиболее удаленных растянутого и сжатого волокон.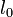 к наименьшему радиусу инерции
к наименьшему радиусу инерции 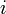 его поперечного сечения.
его поперечного сечения.
 . Стержень с большей гибкостью, при прочих неизменных параметрах, имеет более низкуюпрочность на сжатие и сжатие с изгибом.
. Стержень с большей гибкостью, при прочих неизменных параметрах, имеет более низкуюпрочность на сжатие и сжатие с изгибом. , где
, где — коэффициент, зависящий от условий закрепления стрежня, а
— коэффициент, зависящий от условий закрепления стрежня, а 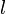 — геометрическая длина. Расчетная длина, также называется привиденной или свободной.
— геометрическая длина. Расчетная длина, также называется привиденной или свободной.


