
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Криволинейные интегралы 1-го и 2-го рода.Содержание книги
Поиск на нашем сайте
Рассмотрим на плоскости Оху некоторую спрямляемую кривую L, не имеющую точек самопересечения и участков самоналегания. Пусть L определяется параметрически Пусть на L=АВ определены 3 функции: f (х, у), Р (х, у), Q (х, у), непрерывные (=> равномерно непрерывные) вдоль L (для f (х, у): для Разобьем [ а, b ]: L распадается на п частичных дуг: Выберем на каждой
Составим 3 интегральные суммы:
где О1. Назовем число I пределом интегральной суммы О2. Если
О3. Если
- общий криволинейныйинтеграл 2-го рода Из определения => криволинейный интеграл 1-го рода не зависит от направления пробега L, а для 2-го рода изменение направления на L ведет к изменению знака
О4. Кривая L называется гладкой, если Особые точки кривой L - точки, соответствующие значению t из [ а, b ]: Т. Если кривая L = AB является гладкой и не содержит особых точек и если f (х, у), Р (х, у), Q (х, у) непрерывны вдоль L, то криволинейные интегралы (41) и (42)
Док-во. Определенные интегралы справа в (51), (52), (53) Разобьем [ а, b ]на п частичных
представим (31) и (32) в виде:
Пусть
При сделанных предположениях о f (х, у), Р (х, у)и ф-х (1) ф-и
=> при Т. о., для
Полагая Δ < δ, получим для (61), (62) оценки:
=> интегральные суммы З. Криволинейные интегралы имеют те же свойства, что и обычные определенные интегралы. 1°. Линейное св-во. Если для f (х, у) и g (х, у)
2°. Аддитивность. Если дуга АВ составлена из двух дуг АС и СВ, не имеющих общих внутренних точек, и если для f (х, у)
3°. Оценка модуля интеграла. Если
4°. Формула среднего значения. Если f (х, у) непрерывна вдоль кривой АВ, то
23. Понятие поверхности. Нормаль и касательная к поверхности. Лемма о проекции окрестности точки на касательную поверхность. О1. Отображение f области G на плоскости на множество G* 3-мерного пр-ва называется гомеоморфным, если это отображение осуществляет взаимно однозначное соответствие между точками G и G*, при котором каждая фундаментальная послед-сть точек G переходит в фундаментальную послед-сть точек G* и, наоборот, каждая фундаментальная послед-сть точек G* является образом фундаментальной послед-сти точек G. О2. Отображение f области G на G * называется локально гомеоморфным, если у каждой точки G есть окрестность, которая гомеоморфно отображается на свой образ. О3. Область G на плоскости Т называется элементарной, если эта область является образом открытого круга D при гомеоморфном отображении этого круга на плоскость Т. О4. Связная область G на плоскости Т называется простой, если О5. Множество точек Ф пр-ва называется поверхностью, если это множество является образом простой плоской области G при локально гомеоморфном отображении f области G в пр-во Е 3. Окрестность точки М поверхности Ф - подмножество точек Ф, принадлежащее окрестности точки М в Е3. Пусть на плоскости (и, v)задана простая область G и для всех точек этой области определены 3 ф-и: или 1 векторная ф-я где 1) ф-и (1) имеют в области G непрерывные частные производные 1-го порядка по и и v; 2)всюду в G rang А = 2, где Утв. При выполнении требований А множество Ф точек, определяемых уравнениями (1), представляет собой поверхность. Док-во. Пусть Из непрерывности ф-й (1) => разность Т.к. в каждой
=> и из А 1): для системы вокрестности =>
Она осуществляет гомеоморфное отображение малой окрестности З1. Поверхность Ф, определяемую уравнениями (1), при выполнении А 1) называют гладкой, а при выполнении А 2) - не имеющей особых точек. З2. Гладкая без особых точек поверхность в достаточно малой окрестности каждой из своих точек однозначно проектируется хотя бы на 1 из трех координатных плоскостей. Пусть поверхность Ф определяется уравнениями (1), для которых выполнены требования А. Геометрический смысл векторной ф-и rang А = 2 => векторы
Поверхности Ф, на которых в целом существует непрерывное поле нормалей, называются двусторонними. Поверхность Ф называется полной, если любая фундаментальная послед-сть точек этой поверхности сходится к точке этой поверхности. Поверхность Ф называется ограниченной, если существует 3-мерный шар, содержащий все точки этой поверхности. Л1. Если Ф - гладкая поверхность и Док-во. Пусть для окрестности
Пусть окрестность Участок поверхности имеет размеры меньше δ (δ > 0), если он лежит внутри шара радиуса δ/2. Л2. Для гладкой ограниченной полной поверхности Ф без особых точек Док-во. Из З2 и Л1 => для В силу З2 и Л1 Л3. Пусть Ф - гладкая без особых точек двусторонняя полная ограниченная поверхность, определяемая уравнениями (1). Тогда для Док-во. Ф двусторонняя => поле нормалей непрерывно => равномерно непрерывно на всей Ф => для
(
то
24. Площадь поверхности. Квадрируемость поверхности.
Пусть Ф - поверхность, определяемая уравнениями Пусть выполнены требования А: 1) ф-и (1) имеют в области G непрерывные частные производные 1-го порядка по и и v; 2)всюду в G rang А = 2, где Поверхность Ф, определяемую уравнениями (1), при выполнении А 1) называют гладкой, а при выполнении А 2) - не имеющей особых точек. Поверхности Ф, на которых в целом существует непрерывное поле нормалей, называются двусторонними. Поверхность Ф называется полной, если любая фундаментальная послед-сть точек этой поверхности сходится к точке этой поверхности. Поверхность Ф называется ограниченной, если существует 3-мерный шар, содержащий все точки этой поверхности. Пусть Ф - гладкая без особых точек ограниченная полная двусторонняя поверхность. С помощью гладких кривых разобьем Ф на конечное число не имеющих общих внутренних точек гладких участков
О1. Число
О2. Если для поверхности Ф Т1. Гладкая ограниченная полная двусторонняя поверхность Ф без особых точек, определяемая уравнениями (1), квадрируема, и для ее площади
Док-во. При условиях Т подынтегральная функция в (3) непрерывна в G и интеграл (3) Фиксируем 1) 2) косинус угла γ между двумя нормалями каждого участка Такой выбор δ > 0 возможен в силу Л* и Л**. Разобьем с помощью гладких кривых поверхность Ф на не имеющие общих внутренних точек частичные участки Для вычисления
Косинус угла
Для точек Если части
=> из (4) и (5)
Применяя к (6) формулу среднего значения***:
где
Просуммируем (8) по i, учитывая
=> используя оценку для
З1. Формула (3) инвариантна относительно выбора осей координат. З2. В общем случае согласно Л*поверхность Ф можно разбить на конечное число частей, каждая из которых определяется своими уравнениями (1) => площадь поверхности можно определить как сумму площадей этих частей. Площадь каждой части можно вычислть по формуле => Т1 *. Гладкая ограниченная полная двусторонняя поверхность без особых точек квадрируема. З3. Если Ф кусочно гладкая, т. е. составлена из конечного числа гладких ограниченных полных двусторонних поверхностей, то Ф квадрируема и ее площадь можно определить как сумму площадей составляющих ее поверхностей. З4. Если обозначить
то, т.к. для
З5. Св-во аддитивности: если Ф разбита кусочно гладкой кривой на части Ф1 и Ф2, не имеющие общих внутренних точек, то площадь Ф равна сумме площадей Ф1 и Ф2. Вытекает из представления площади поверхности с помощью интеграла и аддитивного св-ва интеграла. ------------------------------- *: Для гладкой ограниченной полной поверхности Ф без особых точек **: Пусть Ф - гладкая без особых точек двусторонняя полная ограниченная поверхность, определяемая уравнениями (1). Тогда для ***: Если f (х, у) и g (х, у) интегрируемы в области D, g (х, у) ≥ 0(≤ 0) всюду в D,
то
Если при этом f (х, у) непрерывна в D, а область D связна, то в D
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 581; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.214.244 (0.016 с.) |

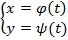 (a ≤ t ≤ b) (1), незамкнута и ограничена точками А и В:
(a ≤ t ≤ b) (1), незамкнута и ограничена точками А и В:  .
. ε > 0
ε > 0 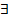 δ > 0:
δ > 0: 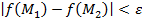 для
для 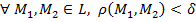 ).
). на п частичных сегментов
на п частичных сегментов 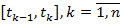 .
. ,где
,где  имеют координаты
имеют координаты  ,
,  .
.
 ,
,  . Пусть
. Пусть  - длина k -й частичной дуги
- длина k -й частичной дуги  :
: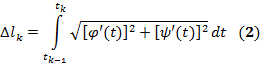





 (s = 1, 2, 3) при
(s = 1, 2, 3) при  , если для
, если для  )
)  , как только Δ < δ.
, как только Δ < δ.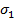 при
при 
 [
[  ] при
] при 


 из определяющих ее уравнений (1) имеют на [ а, b ] непрерывные производные
из определяющих ее уравнений (1) имеют на [ а, b ] непрерывные производные  (т. е. они непрерывны в a < t < b и имеют конечные предельные значения в а справа и в b слева).
(т. е. они непрерывны в a < t < b и имеют конечные предельные значения в а справа и в b слева). . Обыкновенные точки L:
. Обыкновенные точки L:  .
.





 и
и  - определенные интегралы в правых частях (51) и (52), представим их по [ а, b ]в виде суммы п интегралов по
- определенные интегралы в правых частях (51) и (52), представим их по [ а, b ]в виде суммы п интегралов по  . Оценим разности
. Оценим разности

 и
и  как сложные ф-и аргумента t непрерывны на [ а, b ] => равномерно непрерывны на [ а, b ].
как сложные ф-и аргумента t непрерывны на [ а, b ] => равномерно непрерывны на [ а, b ]. и
и  непрерывны на [ а, b ]и ≠ 0 одновременно, то
непрерывны на [ а, b ]и ≠ 0 одновременно, то
 .
. , где l - длина кривой L, а в (62)
, где l - длина кривой L, а в (62)


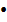
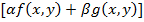 также
также 

 , причем
, причем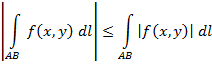
 AB такая что
AB такая что


 - вектор с компонентами
- вектор с компонентами  . Пусть выполнены требования А:
. Пусть выполнены требования А:
 -
-  отображается в малую окрестность
отображается в малую окрестность  , где
, где  .
. можно сделать меньше
можно сделать меньше  => если
=> если  - фундаментальная послед-сть точек в малой окрестности
- фундаментальная послед-сть точек в малой окрестности  , то послед-сть их образов
, то послед-сть их образов  , где
, где  также является фундаментальной в Ф.
также является фундаментальной в Ф.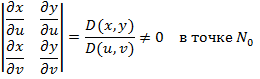

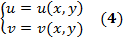
 на малую окрестность точки
на малую окрестность точки  плоскости Оху. (В 1 сторону это отображение задается непрерывными ф-ями (4), а в другую сторону - первыми двумя соотношениями (1), в которых
плоскости Оху. (В 1 сторону это отображение задается непрерывными ф-ями (4), а в другую сторону - первыми двумя соотношениями (1), в которых  также непрерывны; непрерывность всех функций обеспечивает перевод фундаментальной послед-ти в окрестности одной из
также непрерывны; непрерывность всех функций обеспечивает перевод фундаментальной послед-ти в окрестности одной из  в фундаментальную послед-сть в окрестности другой из этих точек.) Подставляя (4) в третью ф-ю (1), получим непрерывную в окрестности
в фундаментальную послед-сть в окрестности другой из этих точек.) Подставляя (4) в третью ф-ю (1), получим непрерывную в окрестности 
 . Т.к. суперпозиция гомеоморфных отображений - гомеоморфное отображение, то гомеоморфно отображение малой окрестности точки
. Т.к. суперпозиция гомеоморфных отображений - гомеоморфное отображение, то гомеоморфно отображение малой окрестности точки  => множество Ф точек, определяемых уравнениями (1), при выполнении требований А является поверхностью.
=> множество Ф точек, определяемых уравнениями (1), при выполнении требований А является поверхностью. из G, то
из G, то  определяет кривую на Ф (координатную линию), вектор
определяет кривую на Ф (координатную линию), вектор  - касательный к этой линии. Аналогично при
- касательный к этой линии. Аналогично при  уравнение
уравнение  определяет другую координатную линию, вектор
определяет другую координатную линию, вектор 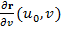 - касательный к ней. Через
- касательный к ней. Через  и
и  линейно независимы, т. е. неколлинеарны => они определяют плоскость, касательную к Ф в
линейно независимы, т. е. неколлинеарны => они определяют плоскость, касательную к Ф в 
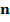 - вектор единичной нормали к Ф. В силу требований, наложенных на ф-и (1),
- вектор единичной нормали к Ф. В силу требований, наложенных на ф-и (1),  точки
точки  , 2) окрестность
, 2) окрестность  .
. => в
=> в  нормали к
нормали к  в точке М. Рассмотрим линию пересечения
в точке М. Рассмотрим линию пересечения 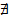 такого δ > 0 => для
такого δ > 0 => для  (n = 1, 2,...)
(n = 1, 2,...)  имеющий размеры <
имеющий размеры < 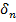 и не проектирующийся однозначно либо на 1 из координатных плоскостей, либо на касательную плоскость, проходящую через некоторую
и не проектирующийся однозначно либо на 1 из координатных плоскостей, либо на касательную плоскость, проходящую через некоторую  . Выберем в каждой части
. Выберем в каждой части  и выделим из послед-сти
и выделим из послед-сти  точек ограниченной полной поверхности Ф подпослед-сть
точек ограниченной полной поверхности Ф подпослед-сть  , сходящуюся к некоторой
, сходящуюся к некоторой 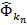 ,начиная с некоторого
,начиная с некоторого  ,попадут внутрь
,попадут внутрь 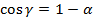 , где 0 ≤ α < ε.
, где 0 ≤ α < ε. и
и  , для которых
, для которых  , справедливо неравенство
, справедливо неравенство
 , а величина
, а величина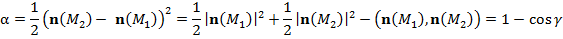
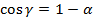 и для α в силу (8):
и для α в силу (8):


 , имеющих размер < δ, где δ достаточно мало и определяется условиями Л*. Пусть диаметр разбиения Δ - максимальный из размеров
, имеющих размер < δ, где δ достаточно мало и определяется условиями Л*. Пусть диаметр разбиения Δ - максимальный из размеров 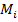 и спроектируем
и спроектируем  - площадь проекции
- площадь проекции 
 называется пределом сумм (2) при
называется пределом сумм (2) при  , независимо от выбора
, независимо от выбора 

 , где
, где  и
и  (
( имеет координаты { А, В, С }, где
имеет координаты { А, В, С }, где
 между нормалью в точке М участка
между нормалью в точке М участка 
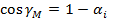 .
. простой плоской области G, то, используя формулу для площади плоской области при переходе от координат (х, у)к координатам (и, v)с помощью соотношений
простой плоской области G, то, используя формулу для площади плоской области при переходе от координат (х, у)к координатам (и, v)с помощью соотношений  ,получим
,получим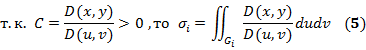


 - некоторая точка
- некоторая точка  в (7):
в (7):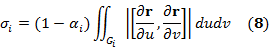

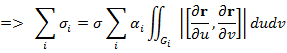
 :
:

 , получим
, получим

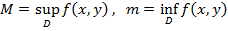
 такое, что:
такое, что:
 .
.


