
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поверхностные интегралы первого и второго рода.Содержание книги
Поиск на нашем сайте
Пусть Ф - поверхность, определяемая уравнениями Пусть выполнены требования А: 1) ф-и (1) имеют в области G непрерывные частные производные 1-го порядка по и и v; 2)всюду в G rang А = 2, где Поверхность Ф, определяемую уравнениями (1), при выполнении А 1) называют гладкой, а при выполнении А 2) - не имеющей особых точек. Поверхности Ф, на которых в целом существует непрерывное поле нормалей, называются двусторонними. Поверхность Ф называется полной, если любая фундаментальная послед-сть точек этой поверхности сходится к точке этой поверхности. Поверхность Ф называется ограниченной, если существует 3-мерный шар, содержащий все точки этой поверхности. Пусть Ф - гладкая без особых точек ограниченная полная двусторонняя поверхность, определяемая уравнениями (1) в области G. Пусть на Ф определены 4 функции: f (х, у, z), Р (х, у, z), Q (х, у, z), R (х, у, z), непрерывные (=> равномерно непрерывные) на множестве точек Ф. Разобьем Ф при помощи гладких или кусочно гладких кривых на конечное число частичных поверхностей Пусть n (
где
О1. Число О2. Если при
О2 *. Если при
Сумма (32) - (34) называется общим поверхностным интегралом 2-го рода:
где А = А (х, у, z) - вектор с компонентами Р (х, у, z), Q (х, у, z), R (х, у, z), n ={соs Х, соs Y, соs Z} - вектор единичной нормали к поверхности Ф. Изопределений => 1) поверхностный интеграл 1-го рода не зависит от выбора стороны поверхности и не меняется при изменении направления нормали на противоположное, 2-го рода меняют знак; 2) интеграл 1-го рода (31) и общий интеграл 2-го рода (35) не зависят от выбора системы координат и инвариантны относительно перехода к новым координатам; 3) каждый из интегралов 2-го рода (32) - (34) сводится к поверхностному интегралу 1-го рода (31): взять в интеграле 1-го рода f (М)соответственно равной
Т. Если Ф гладкая двусторонняя полная ограниченная поверхность без особых точек, задаваемая уравнениями (1), а функция f (х, у, z)[ Р (х, у, z), Q (х, у, z), R (х, у, z)] непрерывна вдоль Ф, то поверхностный интеграл (31) [(32) - (34)] существует и сводится к обычному двойному интегралу:
Док-во. Достаточно док-ть только для (31) и (41), т.к. все интегралы 2-го рода сводятся к этому интегралу. Интеграл в правой части (41) (обозначим его
Т.к. f (М)равномерно непрерывна на Ф, то для этого ε > 0
где
при Δ < δ =>
26. Преобразование базисов. Инварианты линейного оператора. Разложение вектора
Пусть О. Базис Утв. Для Док-во. Пусть Т.о., к произвольному базису Рассмотрим переход от биортогональных базисов
( (1), (2) - формулы перехода от старых базисов к новым и обратно.
Преобразования (1) взаимно обратны => ( Но из (1) => => Аналогично Утв. Матрица Док-во. Т.к.
Сл. Для перехода от базисов
Пусть Умножим 1-ое из (6) скалярно на
Подставим в 1-ое (8) вместо а вектор
где Умножим 1-ое из (9) скалярно на
т. е. матрицы Если то из (7) =>
=> координаты
Т.о., координаты а, при переходе от старого базиса Если согласно (7) записать
Из (11) => при переходе к новому базису координаты Рассмотрим 1) 2) 1) Из (9) =>
2) Ан-но, Некоторое выражение называется инвариантом, если оно не меняется при преобразовании базиса пр-ва (напр., скалярное произведение двух векторов). Пусть У1. Величина Док-во. Надо показать, что если перейти к другому базису Из (5) => О1. Инвариант З1. Для построения матрицы ЛО А достаточно задать оператор на базисных векторах
З2. У2. Величина Док-во. Пусть
О2. Инвариант
Пусть в
Через элементы матрицы оператора A. Из (12):
=> Ан-но =>
|
|||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 612; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.142.235 (0.009 с.) |



 , пусть диаметр разбиения Δ - максимальный размер
, пусть диаметр разбиения Δ - максимальный размер  .
.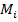 ) - единичная нормаль в точке
) - единичная нормаль в точке  - ее направляющие косинусы). Пусть
- ее направляющие косинусы). Пусть  - площадь
- площадь 


 - подобласть G, образом которой является
- подобласть G, образом которой является 
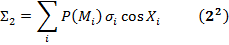
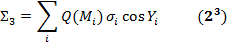
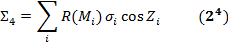
 (k = 1, 2, 3, 4) называется пределом сумм
(k = 1, 2, 3, 4) называется пределом сумм  при
при  , если для
, если для  ε > 0
ε > 0 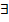 δ = δ(Δ) > 0 такое, что при
δ = δ(Δ) > 0 такое, что при  (независимо от выбора
(независимо от выбора  ) выполняется
) выполняется 
 , то этот предел называется поверхностным интегралом 1-го рода от f (х, у, z) по поверхности Ф:
, то этот предел называется поверхностным интегралом 1-го рода от f (х, у, z) по поверхности Ф: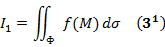


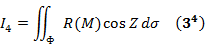

 и
и  , причем если Р, Q и R являются непрерывными на Ф, то и f окажется непрерывной вдоль Ф.
, причем если Р, Q и R являются непрерывными на Ф, то и f окажется непрерывной вдоль Ф.



 , существует (т.к. подынтегральная функция непрерывна) => достаточно доказать, что предел сумм (21) при диаметре разбиения
, существует (т.к. подынтегральная функция непрерывна) => достаточно доказать, что предел сумм (21) при диаметре разбиения  . Фиксируем
. Фиксируем 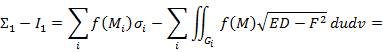
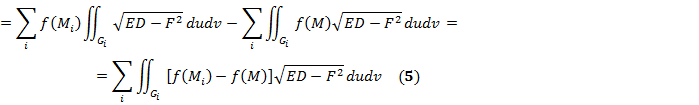
 :
: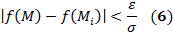
 - площадь поверхности Ф. Из (5), (6) =>
- площадь поверхности Ф. Из (5), (6) =>
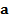 по базису
по базису 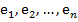 пр-ва
пр-ва 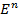 (
( - коэффициенты):
- коэффициенты):
 - базис в n -мерном пространстве
- базис в n -мерном пространстве 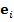 - линейно независимые векторы.
- линейно независимые векторы. - биортогональный к базису
- биортогональный к базису 
 биортогональный базис
биортогональный базис  . Взяв из ортогонального дополнения к
. Взяв из ортогонального дополнения к  , нормированный условием
, нормированный условием  , найдем
, найдем  . Векторы
. Векторы  также образуют базис
также образуют базис 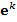 из системы
из системы  векторов
векторов  =>
=>  (т.к.
(т.к.  при
при  ). Но этого не может быть, т.к. по построению
). Но этого не может быть, т.к. по построению  .
. , то
, то  для всех
для всех  =>
=>  , т.к. если некоторый вектор ортогонален всем векторам базиса, то он ортогонален и самому себе => является нулевым вектором.
, т.к. если некоторый вектор ортогонален всем векторам базиса, то он ортогонален и самому себе => является нулевым вектором. 
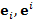 к новым биортогональным базисам
к новым биортогональным базисам 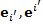 . Разложения базисных векторов:
. Разложения базисных векторов:

 ), (
), ( ) - матрицы прямого и обратного перехода от
) - матрицы прямого и обратного перехода от  , (
, ( )и (
)и ( ) - от
) - от  .
. , а 2-ое - на
, а 2-ое - на  .
.
 , т. е. матрицы
, т. е. матрицы  и
и  взаимно обратны.
взаимно обратны. и
и  взаимно обратны.
взаимно обратны.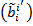 тоже, достаточно доказать
тоже, достаточно доказать  .
.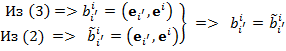


 :
: 



 , а 2-ое - на
, а 2-ое - на 
 и
и  взаимно обратны и по построению в силу симметрии скалярного произведения симметричны.
взаимно обратны и по построению в силу симметрии скалярного произведения симметричны.
 . Подставим в правую часть вместо
. Подставим в правую часть вместо 
 вектора а, разложенного по базису
вектора а, разложенного по базису 
 - координаты а в разложении по биортогональному базису
- координаты а в разложении по биортогональному базису  .
. и подставить вместо
и подставить вместо 
 ) преобразуются с помощью матрицы
) преобразуются с помощью матрицы 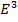 . Пусть
. Пусть  ;
; (векторное).
(векторное). => (т.к. (
=> (т.к. ( и
и 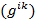 взаимно обратны и симметричны)
взаимно обратны и симметричны)

 (или ей равная
(или ей равная 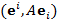 ) - инвариант.
) - инвариант. .
. ,
,  , где
, где 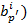 - обратная ей матрица =>
- обратная ей матрица => 
 .
. . Разложим
. Разложим 
 - матрица ЛО A в базисе
- матрица ЛО A в базисе 
 - матричный след оператора А,он равен сумме собственных чисел оператора A с учетом их кратности:
- матричный след оператора А,он равен сумме собственных чисел оператора A с учетом их кратности:  , где
, где  - занумерованные с учетом их кратности собственные числа оператора А. Сумма
- занумерованные с учетом их кратности собственные числа оператора А. Сумма  не зависит от выбора базиса пространства =>
не зависит от выбора базиса пространства =>  не зависит от выбора базиса, т. е. является инвариантом.
не зависит от выбора базиса, т. е. является инвариантом. (или ей равная
(или ей равная  ) - инвариант.
) - инвариант.













