
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема Арцела. Признак равностепенной непрерывности функциональной последовательности.Содержание книги
Поиск на нашем сайте О1. Функц. послед-сть { fn (x)} сходится к функции f (х) равномерно на { х }, если для О2. Функц. послед-сть { fn (x)} называется равномерно ограниченной на { x }, если Пусть каждая fn (x)из { fn (x)}определена на некотором плотном в себе { x } пр-ва Ет. О3. Послед-сть { fn (x)} называется равностепенно непрерывной на { х }, если для справедливо для всех п и всех х' и х" Из определения => если вся { fn (x)}равностепенно непрерывна на { х }, то и Т1 (теорема Арцела). Если { fn (x)} равностепенно непрерывна и равномерно ограничена на [ а, b ], то из этой послед-сти можно выделить подпослед-сть, сходящуюся равномерно на [ а, b ]. Док ̶ во. Рассмотрим на [ а, b ]специальную послед-сть точек { xn }: х 1делит [ а, b ]на 2 равные части; х 2и х 3 вместе с х 1делят [ а, b ]на 4 равные части; х 4, х 5, х 6и х 7вместе с х 1, х 2и х 3делят [ а, b ]на 8 равных частей и т. д. Построенная послед-сть всюду плотная на [ а, b ]: для Выделим из { fn (x)} равномерно на сегменте [ а, b ]сходящуюся подпоследовательность. Рассмотрим { fn (x)} в точке х 1. Получим ограниченную числовую послед-сть { fn (х 1)}, из которой по Т. Больцано - Вейерштрасса можно выделить сходящуюся подпослед-сть: Далее рассмотрим функц. послед-сть => функц. послед-сть сходится и в х 1, и в х 2. Продолжая, получим бесконечное множество подпослед-стей
………………………………
……………………………… причем подпослед-сть, стоящая в n ̶ й строке, сходится в каждой из х 1, х 2 ,..., хп. «Диагональную» послед-сть Докажем, что она равномерно сходится на [ а, b ]. Фиксируем
Разобьем [ а, b ]на конечное число отрезков длины < δ. Из { хп }выберем конечное число п 01-х членов х 1, х 2, ..., хп 0настолько большое, чтобы в каждом из этихх отрезков содержалась хотя бы 1 из точек х 1, х 2, ..., хп 0 . Диагональная послед-сть сходится в каждой х 1, х 2, ..., хп 0 => для фиксированного выше ε > 0 для всех п ≥ N, всех р Пусть х - Т.к. модуль суммы не превосходит суммы модулей:
=> (3) + (4) +(3) + условие | х - хт| < δ: для для всех п ≥ N, всех р З1. В Т. Арцела вместо равномерной ограниченности { fn (x)} на [ а, b ]достаточно потребовать ограниченности { fn (x)} хотя бы в 1 точке [ а, b ]: если { fn (x)} равностепенно непрерывна на [ а, b ] и ограничена хотя бы в 1 точке х 0[ а, b ], то { fn (x)} равномерно ограничена на [ а, b ]. Док-во. По определению равностепенной непрерывности для ε = 1 З2. Достаточный признак равностепенной непрерывности: если { fn (x)} состоит из дифференцируемых на [ а, b ] функций и если { fn ' (x)} равномерно ограничена на [ а, b ], то { fn (x)} равностепенно непрерывна на [ а, b ]. Док-во. Возьмем на [ а, b ]2
Т.к. { fn ' (x)} равномерно ограничена на [ а, b ] => Подставляя (7) в (6): Фиксируем 16. Степенные ряды. Теорема Коши ̶ Адамара. Непрерывность суммы, почленное интегр-ние и дифф-ние степенного ряда. Разложение функций в степенные ряды. Определения сходимости??? Степенной ряд - функц. ряд вида (
Числовая послед-сть из коэффициентов аn: 2 случая: 1) (2) неограничена; 2) (2) ограничена => у (2) Т1 (Коши - Адамара). I. Если (2) не ограничена, то степенной ряд (1) сходится лишь при х = 0. II. Если (2) ограничена и имеет верхний предел L > 0, то ряд (1) абсолютно сходится для х, удовлетворяющих |х| < 1 / L, и расходится для х, удовлетворяющих |х| > 1 / L. III. Если (2) ограничена и ее верхний предел L = 0, то ряд (1) абсолютно сходится для всех х. Док-во. I. (2) не ограничена => при х ≠ 0посл-сть II. (2) ограничена и ее верхний предел L > 0. а) Фиксируем
=> ряд (1) абсолютно сходится по признаку Коши (3*). б) Фиксируем
=> нарушено необходимое условие сходимости (2*) ряда (1) => (1) расходится. III. (2) ограничена и ее верхний предел L = 0. Фиксируем
=> ряд (1) абсолютно сходится к признаку Коши (3*). Т2. Для каждого степенного ряда (1), если он не является рядом, сходящимся лишь в точке х = 0, R - радиус сходимости степенного ряда, (- R, R) - промежуток сходимости. Вычисляется:
З1. На концах (- R, R) степенной ряд может быть как сходящимся, так и расходящимся. Пусть ряд (1) имеет радиус сходимости R > 0. Л. Каково бы ни было 0 < r < R, ряд (1) равномерно сходится на [- r, +r ], т.е. при |х| < r. Док-во. По Т2 ряд (1) абсолютно сходится при x = r, т. е. сходится ряд
По признаку Вейерштрасса (4*) ряд (1) сходится равномерно на [- r, +r ]. Сл1. В условиях леммы сумма ряда (1) является функцией, непрерывной на [- r, +r ]. (По (Т(7*)). Т 3. Сумма степенного ряда внутри его промежутка сходимости - непрерывная функция. Док-во. Пусть S (x) - сумма ряда (1), R - его радиус сходимости. Фиксируем Т4. Если R > 0 - радиус сходимости ряда (1), а х удовлетворяет условию | х| < R, то ряд (1) можно почленно интегрировать на [0, х ]. Полученный в результате почленного интегрирования ряд имеет тот же радиус сходимости R, что и исходный ряд. Док-во. Для
радиус сходимости которого (по (3)) - величина, обратная верхнему пределу последовательности
Т4 доказана, так как верхний предел послед-сти (4) тот же, что и у (2):
Т5. Степенной ряд (1) внутри его промежутка сходимости можно дифференцировать почленно. Ряд, полученный почленным дифференцированием, имеет тот же радиус сходимости, что и исходный ряд. Док-во. Достаточно (по Т(6*) и леммы) доказать лишь второе утверждение теоремы. В результате почленного дифференцирования (1) получим ряд
радиус сходимости R которого (по (3)) обратен верхнему пределу последовательности
Теорема доказана, так как последовательность (5) имеет тот же верхний предел, что и (2):
Сл2. Степенной ряд внутри его промежутка сходимости можно дифференцировать почленно сколько угодно раз. Ряд, полученный п-кратным почленным дифференцированием исходного степенного ряда, имеет тот же радиус сходимости, что и исходный ряд. О1. Функция f (х) на (- R, +R)(на { х }) может быть разложена в степенной ряд, если Утв1. Чтобы f (х) могла быть разложена в степенной ряд на (- R, +R), необходимо, чтобы эта функция имела на (- R, +R) непрерывные производные Док-во. Степенной ряд внутри его промежутка сходимости, который во всяком случае содержит (- R, +R), можно почленно дифференцировать сколько угодно раз, причем все полученные при этом ряды сходятся внутри того же промежутка сходимости (Т5) => суммы рядов, полученных сколь угодно кратным дифференцированием (по Т3), являются функциями, непрерывными внутри указанного промежутка сходимости => непрерывными на (- R, +R). Утв2. Если f (х) может быть на (- R, +R) разложена в степенной ряд, то лишь единственным образом. Док-во. Пусть f (х)может быть разложена на (- R, +R)в степенной ряд (1). Дифференцируя этот ряд почленно п раз:
=> коэффициенты степенного ряда (1), в который может быть разложена функция f (х), однозначно определяются формулой (6). • Пусть f (х)имеет на (- R, +R)непрерывные производные О2. Степенной ряд (1), коэффициенты которого определяются формулой (6), называется рядом Тейлора функции f (х). Утв3. Если функция f (х) может быть разложена на (- R, +R) в степенной ряд, то этот ряд является рядом Тейлора функции f (х). (Следует из Утв2) Утв4. Чтобы функция f (х) могла быть разложена в ряд Тейлора на (- R, +R)(на { х }), необходимо и достаточно, чтобы остаточный член в формуле Маклорена для этой функции стремился к 0 на (- R, +R)(на { х }). Остаточные члены в формуле Маклорена для
*: У всякой ограниченной послед-сти 2*: Для сходимости ряда 3*: Если для всех номеров k, по крайней мере начиная с некоторого номера, справедливо неравенство 4 *: Если функц. ряд 5*: Если функц. ряд
6*: Если каждая функция сходится равномерно на [ а, b ], а сам ряд 7*: Если функц. ряд
то и сумма ряда S (х) имеет в
Сл1. Если в условиях Т потребовать, чтобы
|
||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 1098; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.01 с.) |

 ε > 0
ε > 0 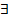 N= N (ε): для всех п (п ≥ N (ε)), и для всех х
N= N (ε): для всех п (п ≥ N (ε)), и для всех х  { х }:
{ х }: 
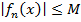
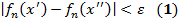
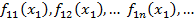
 в точке х 2. По Т. Больцано- Вейерштрасса из нее выделим сходящуюся подпослед-сть:
в точке х 2. По Т. Больцано- Вейерштрасса из нее выделим сходящуюся подпослед-сть: 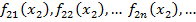


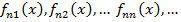
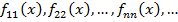 обозначим:
обозначим: 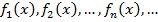
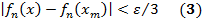
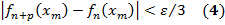
 и всех т =1, 2, …, п 0.
и всех т =1, 2, …, п 0.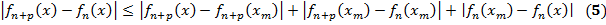
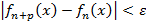
 , выражающего ограниченность { fn (x)}в х 0 =>
, выражающего ограниченность { fn (x)}в х 0 =>  , справедливое для
, справедливое для 
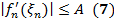
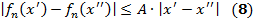
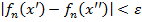 => равностепенная непрерывность { fn (x)}.
=> равностепенная непрерывность { fn (x)}.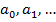 - постоянные веществ. числа)
- постоянные веществ. числа)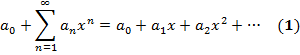
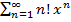 ).
).
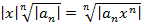 не ограничена => у нее имеются члены со сколь угодно большими п, удовлетворяющие
не ограничена => у нее имеются члены со сколь угодно большими п, удовлетворяющие 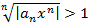 =>
=> 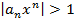 => для (1) (при х ≠ 0) нарушено необходимое условие сходимости (2*) => (1) расходится при х ≠ 0.
=> для (1) (при х ≠ 0) нарушено необходимое условие сходимости (2*) => (1) расходится при х ≠ 0. , начиная с некоторого п, удовлетворяют:
, начиная с некоторого п, удовлетворяют:  => начиная с этого n:
=> начиная с этого n: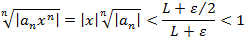
 , (k = 1, 2,...) => начиная с некоторого k:
, (k = 1, 2,...) => начиная с некоторого k: 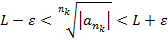 => начиная с этого k:
=> начиная с этого k: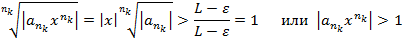


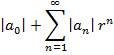

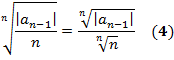
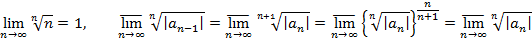
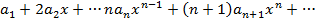

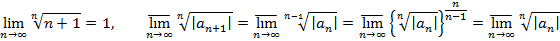
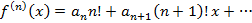

 стремятся к 0 на всей числовой прямой, для
стремятся к 0 на всей числовой прямой, для  - на
- на  => из Утв4:
=> из Утв4: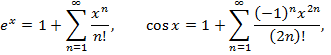
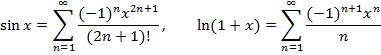
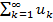 необходимо, чтобы послед-сть и 1, и 2, …, иk,... членов этого ряда являлась бесконечно малой.
необходимо, чтобы послед-сть и 1, и 2, …, иk,... членов этого ряда являлась бесконечно малой.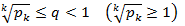 , то ряд
, то ряд 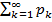 сходится (расходится).
сходится (расходится).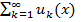 определен на { х } пр-ва Ет и если
определен на { х } пр-ва Ет и если 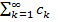 такой, что для всех х
такой, что для всех х 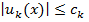 , то ряд
, то ряд 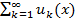 сходится равномерно на { х }.
сходится равномерно на { х }.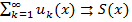 на [ а, b ] и если каждый член ряда
на [ а, b ] и если каждый член ряда 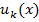 является функцией, интегрируемой на [ а, b ], то и сумма S (х) интегрируема на [ а, b ], причем этот ряд можно интегрировать на [ а, b ] почленно, т. е. сходится числовой ряд
является функцией, интегрируемой на [ а, b ], то и сумма S (х) интегрируема на [ а, b ], причем этот ряд можно интегрировать на [ а, b ] почленно, т. е. сходится числовой ряд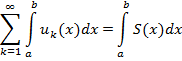
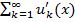
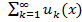 сходится хотя бы в одной точке х 0
сходится хотя бы в одной точке х 0 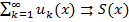 на сегменте [ а, b ], причем этот ряд можно дифф-вать на [ а, b ] почленно, т. е. его сумма S (х) имеет производную:
на сегменте [ а, b ], причем этот ряд можно дифф-вать на [ а, b ] почленно, т. е. его сумма S (х) имеет производную:  .
.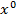
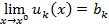
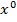 предел, и к пределу можно переходить почленно:
предел, и к пределу можно переходить почленно:



