
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ТЕМА 7. Определенный интегралСодержание книги
Поиск на нашем сайте
Литература: [1. Гл. VI, §1-5,6 (п. 1)]; [2. Гл. IX]; [6. Гл. XI, XII]
Вопросы для самопроверки
1. Что называется определенным интегралом? 2. Связь определенного и неопределенного интегралов. 3. Свойства определенного интеграла. Определенный интеграл это число
ЗАДАЧИ Вычислить определенные интегралы. 1)
2)
ТЕМА 8. Функции нескольких переменных Литература: [1. Гл. X, Дополнение III]; [7. Гл. VII]; [2. Гл. XI]; [6. Гл. VIII]
Вопросы для самопроверки
1. Определение функции двух переменных. 2. Частное и полное приращения функции двух переменных. 3. Частные производные функций двух переменных. 4. Необходимое условие экстремума функций двух переменных. 5. Достаточное условие экстремума функций двух переменных.
Необходимое условие экстремума функций двух переменных в критической точке
Достаточное условие экстремума функций двух переменных в критической точке
Если 1) 2) 3) 4)
ЗАДАЧА Найти экстремум функции и точки экстремума функции z = z (x; y). Определить вид экстремума (минимум или максимум). Решение. 1) Необходимое условие экстремума функции:
2) Достаточное условие экстремума функций двух переменных в критической точке
Ответ: точка минимума
ТЕМА 9. Дифференциальные уравнения Литература: [1. Гл. XI]; [2. Гл. XII]; [6. Гл. XII]
Вопросы для самопроверки
1. Какое уравнение называется дифференциальным? 2. Что называется порядком дифференциального уравнения? 3. Что называется решением дифференциального уравнения? 4. Какое решение дифференциального уравнения называется общим и какое – частным? Каков их геометрический смысл? 5. Какое дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, уравнением с разделенными переменными и как оно решается? 6. Какое дифференциальное уравнение 1-го порядка называется линейным неоднородным уравнением? 7. Метод Бернулли решения линейного неоднородного уравнения 1-го порядка.
ЗАДАЧИ 1. Решить уравнение: Решение.
Ответ: Общее решение в неявном виде
2. Решить уравнение Решение. Преобразуем это уравнение к виду неоднородное дифференциальное уравнение 1-го порядка вида
6) Ответ: Общее решение в явном виде:
ТЕМА 10. Двойной интеграл Литература: [1. Гл. XII]; [2. Гл. XIII]; [6. Гл. XIV]
Вопросы для самопроверки
1. Стандартная область 2. Правило вычисления двойного интеграла по стандартной области 1-го типа. 3. Стандартная область 4. Правило вычисления двойного интеграла по стандартной области 2-го типа. 5. Цилиндроид. 6. Связь двойного интеграла и объема цилиндроида. 7. Связь двойного интеграла и площади области
Область
Рисунок 3
Аналитически область D задается с помощью метода сечений:
Правило вычисления двойного интеграла от функции
где слева в (1) стоит двойной кратный интеграл, а справа – двойной повторный интеграл. В двойном повторном интеграле сначала вычисляется внутренний интеграл по y при фиксированном x, а потом – внешний по x. Аналогичным образом определяется стандартная область
ЗАДАЧА Вычислить двойной интеграл, если область D ограничена указанными линиями.
Решение. Область
Ответ:
ТЕМА 11. Ряды Литература: [1. Гл. XIII]; [2. Гл. XIV]; [6. Гл. XVI]
Вопросы для самопроверки
1. Что называется рядом? В каком случае ряд называется сходящимся, а в каком – расходящимся? Что называется суммой ряда? 2. Почему при исследовании сходимости ряда можно отбрасывать любое конечное число начальных членов? 3. Необходимый признак сходимости рядов. 4. Достаточные признаки сходимости рядов: признак Даламбера; Коши, интегральный, 2-й признак сравнения. 5. Знакочередующиеся ряды. Признак Лейбница. 6. Степенной ряд. Область сходимости и радиус сходимости степенного ряда Числовым рядом называется бесконечная сумма: Необходимый признак сходимости ряда. Если: 1) 2) Признак Даламбера. Если для
Признак Коши. Если для
Интегральный признак. Числовой ряд 2-й признак сравнения. Если для рядов Ряд Знакочередующий ряд: Признак Лейбница сходимости знакочередующего ряда. Если: 1) Степенной ряд Интервал сходимости степенного ряда ЗАДАЧИ 1) Исследовать сходимость числового ряда Решение. Так как
2) Исследовать сходимость числового ряда Решение. Так как
3) Исследовать сходимость числового ряда Решение. Исследуем ряд по интегральному признаку. Так как
4) Исследовать сходимость числового ряда Решение. Исследуем ряд по 2-му признаку сравнения. В качестве эталона рассмотрим похожий ряд
5) Найти область сходимости степенного ряда. Решение. Найдем параметры степенного ряда: Интервал сходимости степенного ряда равен 1) Подставим в степенной ряд
2) Подставим в степенной ряд
Ответ: область сходимости степенного ряда равна D =[2,20).
|
||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 345; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.45.29 (0.006 с.) |

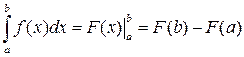 , где F (x) это первообразная для f (x):
, где F (x) это первообразная для f (x):  ; a, b – нижний и верхний пределы интегрирования. Связь определенного и неопределенного интегралов:
; a, b – нижний и верхний пределы интегрирования. Связь определенного и неопределенного интегралов:  , то есть, по сути, вычисление определенного интеграла сводится к вычислению неопределенного интеграла.
, то есть, по сути, вычисление определенного интеграла сводится к вычислению неопределенного интеграла.
 .
.
 .
. :
:
 :
:


 экстремума нет;
экстремума нет; неопределенность.
неопределенность.



 Получили критическую точку
Получили критическую точку  .
.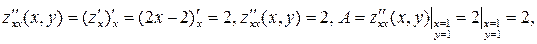


 Так как
Так как  , то точка
, то точка  является точкой минимума. Экстремум функции – это минимум функции и он равен
является точкой минимума. Экстремум функции – это минимум функции и он равен  .
. .
. .
. Это уравнение с разделяющимися переменными. Путем разделения переменных приведем его к виду уравнения
Это уравнение с разделяющимися переменными. Путем разделения переменных приведем его к виду уравнения 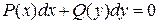 с разделенными переменными:
с разделенными переменными:  После интегрирования получим:
После интегрирования получим: 



 .
. .
. . Это линейное
. Это линейное . Оно решается методом Бернулли.
. Оно решается методом Бернулли. ,
,  – новые неизвестные функции.
– новые неизвестные функции. 
 . Вынесем слева
. Вынесем слева  за скобки:
за скобки:  . Так как неизвестных
. Так как неизвестных  две, а уравнение одно, то еще одно условие можно выбрать произвольно. Потребуем, чтобы выражение в скобке равнялась нулю. 4) Получим уравнение
две, а уравнение одно, то еще одно условие можно выбрать произвольно. Потребуем, чтобы выражение в скобке равнялась нулю. 4) Получим уравнение  с разделяющимися переменными,
с разделяющимися переменными, 


 Общее решение исходного уравнения 1-го порядка содержит одну произвольную постоянную, поэтому зафиксируем
Общее решение исходного уравнения 1-го порядка содержит одну произвольную постоянную, поэтому зафиксируем 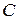 , например,
, например, 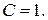 Следовательно,
Следовательно,  . 5) В уравнение
. 5) В уравнение 



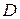 1-го типа в плоскости
1-го типа в плоскости  .
.
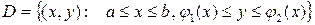 .
. по стандартной области D 1-го типа в плоскости
по стандартной области D 1-го типа в плоскости 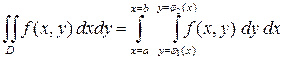 (1)
(1) для нее направлена вверх, а ось
для нее направлена вверх, а ось  направлена вправо.
направлена вправо. , D:
, D:  .
.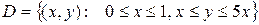 . По правилу вычисления двойного интеграла по стандартной области D 1-го типа в плоскости
. По правилу вычисления двойного интеграла по стандартной области D 1-го типа в плоскости 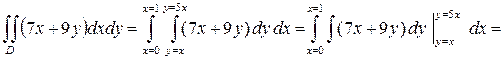

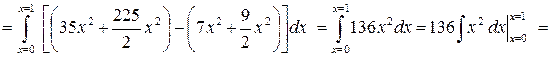

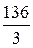 .
.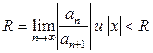 .
. , где
, где  – общий член ряда. Если бесконечная сумма существует и конечна, то говорят, что числовой ряд сходится, в противном случае – расходится.
– общий член ряда. Если бесконечная сумма существует и конечна, то говорят, что числовой ряд сходится, в противном случае – расходится.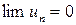 при
при 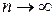 , то ряд может сходиться или расходиться;
, то ряд может сходиться или расходиться; при
при  существует предел:
существует предел: при
при 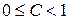 ряд сходится; при
ряд сходится; при  ряд расходится, при
ряд расходится, при 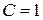 имеется неопределенность.
имеется неопределенность.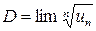 при
при 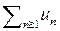 сходится или расходится одновременно с несобственным интегралом
сходится или расходится одновременно с несобственным интегралом 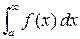 , где
, где  , число
, число 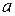 выбирается произвольно, лишь бы под интегралом не было деления на 0.
выбирается произвольно, лишь бы под интегралом не было деления на 0.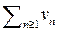 существует предел
существует предел 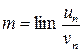 при
при 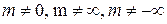 , то ряды сходятся или расходятся одновременно.
, то ряды сходятся или расходятся одновременно.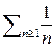 расходится; 2) обобщенный гармонический ряд
расходится; 2) обобщенный гармонический ряд  сходится при
сходится при 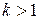 , расходится при
, расходится при 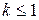 ; 3)
; 3) 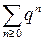 – бесконечная геометрическая прогрессия, при
– бесконечная геометрическая прогрессия, при 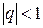 ряд сходится, при
ряд сходится, при  ряд расходится.
ряд расходится.
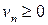 ; 2)
; 2)  монотонно убывают, то есть
монотонно убывают, то есть 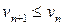 ; 3)
; 3) 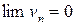 при
при  , где
, где 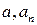 – коэффициенты степенного ряда.
– коэффициенты степенного ряда.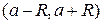 , где R – радиус сходимости степенного ряда можно находить по формуле Даламбера
, где R – радиус сходимости степенного ряда можно находить по формуле Даламбера  или по формуле Коши
или по формуле Коши  при
при  .
. содержит «n факториал» – произведение всех чисел от одного до n:
содержит «n факториал» – произведение всех чисел от одного до n:  , то сходимость ряда исследуется по признаку Даламбера. Заметим, что
, то сходимость ряда исследуется по признаку Даламбера. Заметим, что 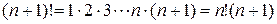 . Найдем
. Найдем 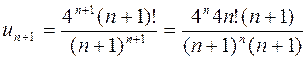 . По признаку Даламбера надо вычислить предел
. По признаку Даламбера надо вычислить предел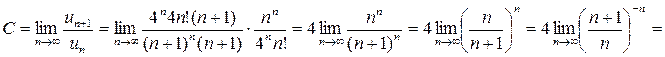
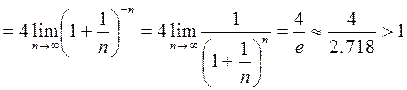 , так как по 2-му замечательному пределу
, так как по 2-му замечательному пределу 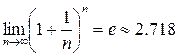 . Так как
. Так как  .
.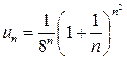 содержит только степени, то сходимость ряда исследуется по признаку Коши:
содержит только степени, то сходимость ряда исследуется по признаку Коши:
 . Так как
. Так как  , то ряд сходится.
, то ряд сходится. .
. , то
, то  . Числовой ряд
. Числовой ряд 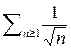 сходится или расходится одновременно с несобственным интегралом
сходится или расходится одновременно с несобственным интегралом  . Вычислим несобственный интеграл
. Вычислим несобственный интеграл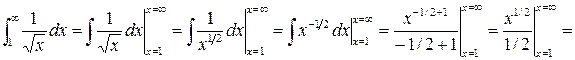
 – несобственный интеграл расходится. Следовательно, исходный числовой ряд расходится.
– несобственный интеграл расходится. Следовательно, исходный числовой ряд расходится. .
. – бесконечная геометрическая прогрессия, расходится. По 2-му признаку сравнения надо найти предел
– бесконечная геометрическая прогрессия, расходится. По 2-му признаку сравнения надо найти предел
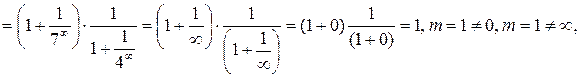
 , следовательно, ряды ведут себя одинаково. Так как эталонный ряд расходится, то исходный ряд тоже расходится.
, следовательно, ряды ведут себя одинаково. Так как эталонный ряд расходится, то исходный ряд тоже расходится. ,
,  . Радиус сходимости ряда вычислим по формуле Даламбера
. Радиус сходимости ряда вычислим по формуле Даламбера 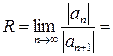

 9, 11+9)=(2,20). Исследуем сходимость ряда в каждой граничной точке
9, 11+9)=(2,20). Исследуем сходимость ряда в каждой граничной точке  и
и  .
. – гармонический ряд, расходится,
– гармонический ряд, расходится,  .
. – знакочередующий ряд,
– знакочередующий ряд,  . По признаку Лейбница: а)
. По признаку Лейбница: а)  . б) Проверим
. б) Проверим  . Затем с помощью арифметических операций преобразуем неравенство к очевидному:
. Затем с помощью арифметических операций преобразуем неравенство к очевидному:  – очевидно верное, значит, исходное неравенство верное. 3)
– очевидно верное, значит, исходное неравенство верное. 3)  . Все три условия признака Лейбница выполняются, следовательно, знакочередующий ряд сходится,
. Все три условия признака Лейбница выполняются, следовательно, знакочередующий ряд сходится,  .
.


