
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2. Аналитическая геометрия на плоскости.Содержание книги
Поиск на нашем сайте
Векторы
Литература: [1. Гл. I, VIII]; [2. Гл. I, II]; [3. Гл. I-X]; [4. Гл. I-IV, VI, VII], [9. Гл. I-V, XVIII]
Вопросы для самопроверки
1. Расстояние между двумя точками и расстояние от точки до прямой. 2. Уравнения прямой линии. 3. Угол между двумя прямыми. 4. Условия параллельности и перпендикулярности прямых. 5. Угловой коэффициент прямой. 6. Что называется координатами вектора? 7. Действия над векторами. 8. Скалярное произведения двух векторов. 9. Векторное произведение двух векторов.
Даны вершины А (2; 5) В (-3; 1); С (0; 2) треугольника. Найти: 1) длину стороны ВС; 2) площадь треугольника (через векторы); 3) уравнение стороны ВС; 4) уравнение высоты, проведенной из вершины А; 5) длину высоты, проведенной из вершины А; 6) угол В в радианах с точностью до 0,01 (через векторы); 7) систему неравенств, определяющих треугольник АВС (рис. 1). Сделать чертеж.
Рисунок 1
Решение. 1) Определим длину стороны ВС по формуле
2) Найдем площадь треугольника АВС, где A (2; 5) В (-3; 1); С (0; 2). В трехмерном пространстве эти точки имеют координаты: A (2; 5; 0), В (-3; 1; 0); С (0; 2; 0).
Векторное произведение
где определитель вычислен по правилу Саррюса. Длина векторного произведения 3) Уравнение стороны ВС, проходящей через точки B (x 1, y 1), С (x 2, y 2), определим по формуле:
4) Уравнение высоты AD составим по формуле у – у 1 = k (x – x 1), где (x 1, y 1) – координаты точки А, k – угловой коэффициент высоты. Координаты точки А известны: А(2;5). Найдем k из условия перпендикулярности прямых Получили уравнение высоты 5) Длину высоты AD определим по следующей формуле:
6) Найдем угол В в радианах с точностью до 0,01. На плоскости векторы
7) Чтобы найти систему неравенств, определяющую треугольник АВС, необходимо составить уравнения всех трех сторон. Уравнение стороны ВС уже составлено: х -3 у + 6 = 0. Составим уравнения прямых АВ и АС:
Так как решением одного неравенства является полуплоскость (геометрически), то возьмем одну из точек этой полуплоскости и подставим в уравнение прямой, этим самым мы определим знак неравенства: Уравнение ВС: х -3 у + 6 = 0, для точки А (2; 5), 2-3×5 + 6 < 0; Уравнение АВ: Уравнение АС: Значит, решением неравенства х -3 у + 6 < 0 является та полуплоскость, в которой находится точка А; решением неравенства Итак, имеем
ТЕМА 3. Введение в анализ Литература: [1. Гл. II]; [2. Гл. V]; [6. Гл. I, II]; [9. Гл. VI-VIII]; [10, Ч. 2. Гл. I];
Вопросы для самопроверки
1. Функция. Область определения функции. 2. Предел переменной величины, предел функции. 3. Неопределенности видов 4. Как связано понятие предела функции с понятиями пределов слева и справа? 5. Непрерывность функции в точке и на отрезке. При вычислении пределов надо в первую очередь определить вид неопределенности. Для этого применяется метод подстановки: надо в функцию подставить число
Если в числителе и знаменателе стоят многочлены, Если в числителе и знаменателе стоят многочлены, Если Если получится неопределенность вида В последнем задании рекомендуется использовать 1-й замечательный предел:
ЗАДАЧИ Найти пределы функций. 1. 2. 3. 4.
5.
|
||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 355; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.102.43 (0.007 с.) |

 ЗАДАЧА
ЗАДАЧА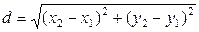
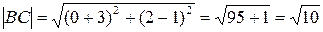 .
. Найдем координаты векторов
Найдем координаты векторов  и
и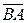 в трехмерном пространстве:
в трехмерном пространстве: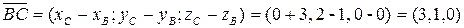 ,
,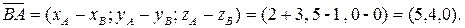
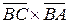 векторов
векторов 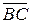 и
и  равно
равно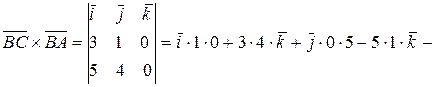
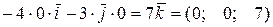 ,
,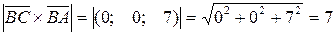 . Площадь треугольника равна
. Площадь треугольника равна  .
. , где x и y –координаты точки (x,y) на [ В,С ].
, где x и y –координаты точки (x,y) на [ В,С ].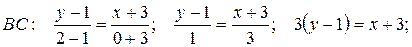 3 у – 3 = х +3, отсюда х -3 у + 6 = 0– общее уравнение стороны ВС.
3 у – 3 = х +3, отсюда х -3 у + 6 = 0– общее уравнение стороны ВС. . Сначала найдем kBC. Уравнение ВС: х -3 у + 6 = 0 приведем к виду BC:
. Сначала найдем kBC. Уравнение ВС: х -3 у + 6 = 0 приведем к виду BC: 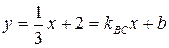 , откуда
, откуда  . Тогда
. Тогда 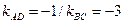 .
.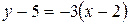 или 3 x + y – 11 = 0.
или 3 x + y – 11 = 0. , где (x 0, y 0) – координаты точки А;
, где (x 0, y 0) – координаты точки А;  – коэффициенты прямой ВС, расстояние до которой мы определяем.
– коэффициенты прямой ВС, расстояние до которой мы определяем. .
.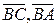 имеют координаты:
имеют координаты: 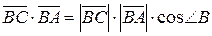 , таким образом,
, таким образом,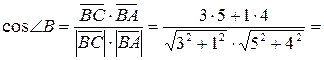
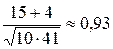 , отсюда ÐB = 0,93 радиан;
, отсюда ÐB = 0,93 радиан; – уравнение стороны АВ.
– уравнение стороны АВ.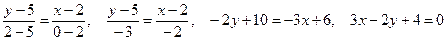 – уравнение стороны АС.
– уравнение стороны АС.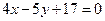 , для точки С (0; 2), -5×1 + 17 > 0;
, для точки С (0; 2), -5×1 + 17 > 0;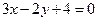 , для точки В (-3; 1), -3×3 - 2×1 + 4 < 0.
, для точки В (-3; 1), -3×3 - 2×1 + 4 < 0. является та полуплоскость, в которой находится точка С, и, наконец, решением неравенства
является та полуплоскость, в которой находится точка С, и, наконец, решением неравенства 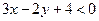 является та полуплоскость, в которой находится точка В, а пересечение всех этих полуплоскостей и определяет треугольник АВС.
является та полуплоскость, в которой находится точка В, а пересечение всех этих полуплоскостей и определяет треугольник АВС.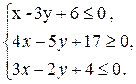
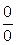 ,
, 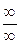 , 1¥ и их раскрытие
, 1¥ и их раскрытие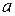 , к которому стремится переменная х:
, к которому стремится переменная х: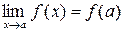 .
.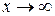 и получится неопределенность вида
и получится неопределенность вида  где
где 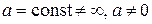 .
.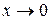 и получится неопределенность вида
и получится неопределенность вида 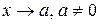 , получится неопределенность вида
, получится неопределенность вида 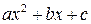 , то квадратные трехчлены разлагаются на множители с помощью формулы
, то квадратные трехчлены разлагаются на множители с помощью формулы 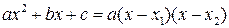 , где
, где 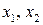 – корни квадратного уравнения
– корни квадратного уравнения  :
: 
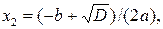
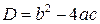 .
.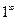 , то необходимо применить формулу 2-го замечательного предела:
, то необходимо применить формулу 2-го замечательного предела:  или
или 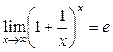 , где е» 2,71.
, где е» 2,71.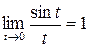 и четыре дополнительных предела:
и четыре дополнительных предела: 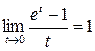 ,
,  ,
, 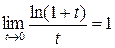 ,
, 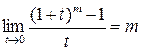 .
. так как
так как 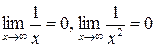 .
.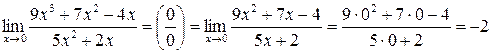 .
.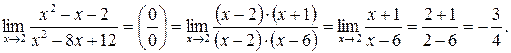

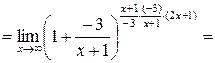
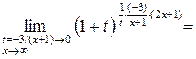
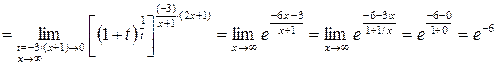 .
.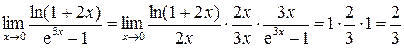 .
.


