
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ТЕМА 4. Производная и дифференциалСодержание книги
Поиск на нашем сайте
Литература: [1. Гл. II]; [2. Гл. V]; [6. Гл. I, II]; [9. Гл. IX-XII]; [10, Ч. 2. Гл. II]
Вопросы для самопроверки
1. Определение производной. 2. Геометрический и механический смысл производной. 3. Правила дифференцирования функций и формулы дифференцирования основных элементарных функций. 4. Производные высших порядков. 5. Что называется дифференциалом функции? 6. Геометрический смысл дифференциала функции.
Основные свойства производной для функций
1. 2. 3. 4. 5. 6. 7. 8. 9.
Таблица элементарных производных
1. 2. 3. 4.
5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19.
ЗАДАЧИ Найти производные заданных функций. a)
b)
c)
d)
e)
ТЕМА 5. Приложения производной Для исследования функций Литература: [1. Гл. III,IV]; [7. Гл. IV]; [2. Гл. VII]; [6. Гл. IV]
Вопросы для самопроверки
1. Каковы признаки возрастания и убывания функции? 2. Что называется экстремумом функции? Как найти максимумы и минимумы функции? 3. Как находятся интервалы выпуклости и вогнутости и точки перегиба графика функции? 4. Что называется асимптотой к кривой? 5. Как находятся вертикальные и наклонные асимптоты графика функции? 6. Общая схема исследования функции и построения ее графика.
Схема исследования функции и построения графика. 1. Находим область определения функции и определяем, не ли у нее точек разрывов. Для каждого бесконечного разрыва учесть знак функции справа и слева. Получим вертикальные асимптоты. 2. Находим точки пересечения графика функции с осями координат. 3. Исследуем функцию на четность f(-x) = f(x) (график функции симметричен относительно оси ОУ) и нечетность f(-x) = -f(x) (график функции симметричен относительно начала координат) 4. Исследуем функцию на экстремум. Находим интервалы возрастания и убывания функции. 5. Исследуем функцию на точки перегиба. Находим интервалы выпуклости и вогнутости. 6. Определяем асимптоты. 7. Берем дополнительные точки (по необходимости). 8. Строим график.
ЗАДАЧА 1. Исследовать средствами дифференциального исчисления функцию Решение 1. Область определения функции (-¥; +¥), то есть функция определена на всей числовой оси. 2. Исследуем на четность f(-x) = f(x) или
Функция ни четная, ни нечетная. Это значит, что график не симметричен относительно осей координат. 3. Исследуем на экстремум:
Итак, точка максимума 4. Исследуем на точки перегиба:
Итак, точка
Найдем точки пересечения с осями. С осью OY: x = 0; Исследуем на асимптоты: данная функция вертикальных асимптот не имеет, так как она определена на всей числовой оси. Попытаемся найти наклонную асимптоту y = kx + b, где
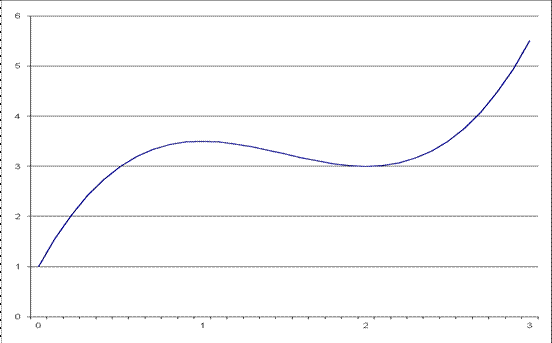
Следовательно, наклонных асимптот функция не имеет. Построим график. График функции показан на рис. 2.
Рисунок 2
ТЕМА 6. Неопределенный интеграл Литература: [1. Гл. V]; [2. Гл. VIII]; [6. Гл. X]
Вопросы для самопроверки
1. Какая функция называется первообразной? 2. Что называется неопределенным интегралом? Каков его геометрический смысл? 3. Свойства неопределенного интеграла. 4. Формула интегрирования по частям. 5. Свойства дифференциала функции. 4. Методы интегрирования.
Таблица основных интегралов: 1. 3. 5. 7. 9. 11. 13. 15. 17. Формула интегрирования по частям: Свойства дифференциала функции 2) 3)
ЗАДАЧИ Найти неопределенные интегралы. Результат проверить дифференцированием. 1)
Проверка:
2) Применим формулу интегрирования по частям:
Проверка:
3) Приравняем знаменатель нулю:
Корни не равны. Интеграл находится по методу неопределенных коэффициентов:
вторая и четвертая дроби равны, равны знаменатели, следовательно равны числители:
Проверка:
4) Приравняем знаменатель нулю:
5) Приравняем знаменатель нулю:
Проверка:
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 476; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.006 с.) |





 .
.






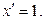
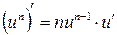

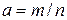





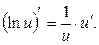
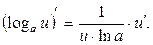

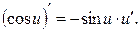
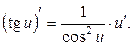


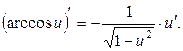

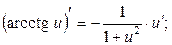
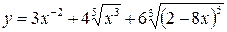 ,
,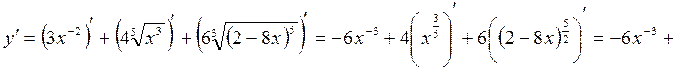
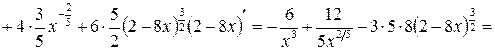
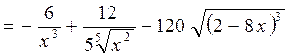 .
.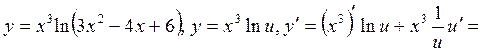
 .
.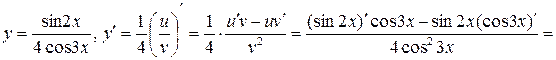
 .
.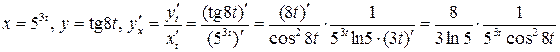 .
.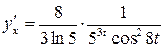 – производная параметрической функции.
– производная параметрической функции.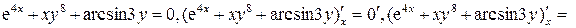
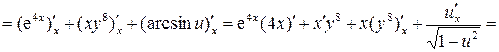
 ,
,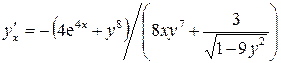 – производная неявной функции.
– производная неявной функции.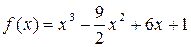 и построить ее график.
и построить ее график.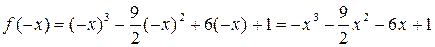 .
. – это точки, подозрительные на экстремум. Исследуем в таблице:
– это точки, подозрительные на экстремум. Исследуем в таблице: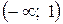
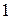
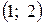





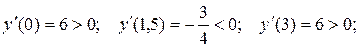
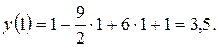

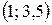 и точка минимума
и точка минимума  .
.

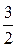


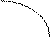



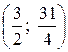 – точка перегиба.
– точка перегиба.
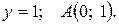
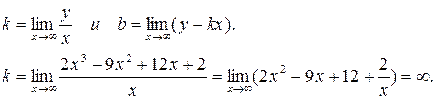

 2.
2. 
 4.
4. 
 6.
6. 
 8.
8. 
 10.
10. 
 12.
12. 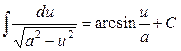
 14.
14. 
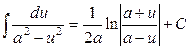 16.
16. 

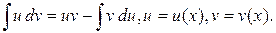
 : 1)
: 1)  ;
; – внесение производной под знак дифференциала;
– внесение производной под знак дифференциала; ; 4)
; 4)  ; 5)
; 5) 
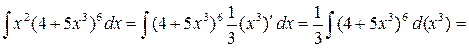
 .
.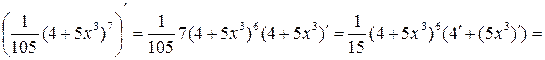
 .
. .
. .
.
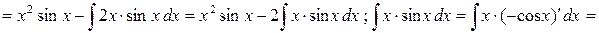


 .
.

 .
. .
. . Найдем корни квадратного уравнения:
. Найдем корни квадратного уравнения: 
 .
. ,
,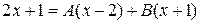 . Пусть
. Пусть 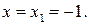 Тогда
Тогда 
 Пусть
Пусть 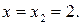 Тогда
Тогда 

 .
.
 .
. .
. . Найдем корни квадратного уравнения:
. Найдем корни квадратного уравнения:  Корни равны
Корни равны  . Интеграл находится по методу разложения:
. Интеграл находится по методу разложения:  ,
,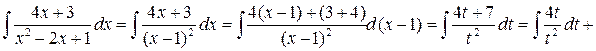
 Проверка:
Проверка: 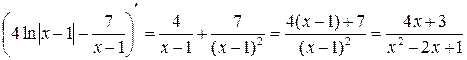 .
. .
. . Вещественных корней нет. Интеграл находится по методу выделения полного квадрата в знаменателе:
. Вещественных корней нет. Интеграл находится по методу выделения полного квадрата в знаменателе: .
.

 ,
,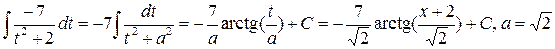 ,
, .
.

 .
.


