
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ТЕМА 1. Определители и системыСодержание книги
Поиск на нашем сайте
МАТЕМАТИКА
Для студентов заочной формы обучения бакалавриата 1 курса Владивосток УДК 378.147 ББК 22.11 М34
Печатается по решению кафедры алгебры, геометрии и анализа Школы естественных наук ДВФУ
Составители: Н.И. Головко, О.В. Бондрова, Д.С. Крылова
Математика: метод. указ. по выполнению контр. работ по дисциплине: для студентов заочной формы обучения 1 курса направлений бакалавриата / Дальневост. федерал. университет; [сост. Н.И. Головко, О.В. Бондрова, Д.С. Крылова]. – Владивосток: Дальневост. федерал. ун-т, 2013. – 40 с.
В методические указания включены задачи по высшей математике с теоретическими пояснениями их решения. Цель данных методических указаний – помочь студентам-заочникам выполнить контрольные работы по высшей математике. Методические указания предназначены для студентов 1 курса ДВФУ заочной формы обучения направлений бакалавриата Школы экономики и менеджмента (080100.62 «Экономика», 080200.62 «Менеджмент», 080400.62 «Управление персоналом», 081100.62 «Государственное и муниципальное управление», 100400.62 «Туризм», 100700.62 «Торговое дело», 100800.62, «Товароведение и экспертиза товаров», 101100.62 «Гостиничное дело»), Школы биомедицины (240700.62 «Биотехнология», 260800.62 «Технология общественного питания»), Инженерной школы(140100.62 «Теплоэнергетика и теплотехника», 130400.65 «Горное дело», 250400.62 «Технология лесозаготовительных и деревообрабатывающих производств»).
Ó Головко Н.И., Бондрова О.В., Крылова Д.С., 2013 ВВЕДЕНИЕ
Настоящие методические указания составлены с целью помочь студенту овладеть основными приемами и методами решения задач по высшей математике. Прежде чем приступить к решению задач по определенной теме, студент должен изучить соответствующий теоретический материал по любому учебнику, указанному ниже (см. список литературы на стр. 5). В начале каждой темы даны основные вопросы и формулы, знание которых необходимо для решения задач. Кроме того, в каждой теме дается решение нескольких заданий, аналогичных тем заданиям, которые предлагаются для самостоятельной работы.
ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ КОНТРОЛЬНЫХ РАБОТ
При выполнении контрольных работ надо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не рецензируются и возвращаются студенту для переработки.
1. Контрольную работу следует выполнять в рукописном виде в тетради, отдельной для каждой работы, чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента. 2. В заголовке работы на обложке тетради должны быть ясно написаны фамилия студента, его инициалы, номер зачетной книжки (шифр), школа ДВФУ, направление и профиль бакалавриата, название дисциплины; номер контрольной работы, здесь же следует указать дату отсылки работы в ДВФУ и адрес студента. В конце работы следует поставить дату ее выполнения и расписаться. 3. В работу должны быть включены все задачи, указанные в задании. Контрольные работы, содержащие не все задачи задания, а также задачи не своего варианта, не рецензируются. 4. Решение задач надо располагать в порядке номеров, указанных в заданиях, сохраняя номера задач. 5. Перед решением каждой задачи надо выписать полностью ее условие. В том случае если несколько задач, из которых студент выбирает задачи своего варианта, имеют общую формулировку, следует, переписывая условия задачи, заменить общие данные конкретными из соответствующего номера. Например, условие задачи 1 должно быть переписано так: Даны вершины А(3;2), В(4;1), С(-1;5) треугольника. Найти: 1) длину стороны ВС и т.д. 6. Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи. 7. После получения прорецензированной работы, как не зачтенной, так и зачтенной, студент должен исправить все отмеченные рецензентом ошибки и недочеты и выполнить все рекомендации рецензента. Если рецензент предлагает внести в решения задач те или иные исправления или дополнения и прислать их для повторной проверки, то это следует сделать в короткий срок в той же тетради. В случае не зачета работы и отсутствия прямого указания рецензента на то, что студент может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново. При высылаемых исправлениях должна обязательно находиться прорецензированная работа и рецензия на нее. В связи с этим рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех дополнений и исправлений в соответствии с указаниями рецензента. Вносить исправления в сам текст работы после ее рецензирования запрещается.
Варианты задач для студентов заочной формы обучения
Номер варианта определяется последней цифрой номера зачетной книжки (шифром) согласно следующей таблице.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. Натансон И. П. Краткий курс высшей математики. М.: Физматгиз, 1963; М.: Наука, 1986; 3-е изд. СПб, 1997. 2. Минорский В. П. Сборник задач по высшей математике. М.: Гостехиздат, 1955–1957; М.: Физматгиз, 1959–1962; М.: Наука, 1964–2006. 3. Ефимов Н. В. Краткий курс аналитической геометрии. М: Физматгиз, 1962–1963; М.: Наука, 1965–1996, 2005. 4. Клетеник Д. В. Сборник задач по аналитической геометрии. М.: Наука, 1965–1980; М.: Гостехиздат, 1954–1956; М.: Физматгиз, 1958–1998. 5. Ефимов Н. В. Квадратичные формы и матрицы. М.: Физматгиз, 1962–163ж. М.: Наука, 1964–1975. 6. Пискунов Н. С. Дифференциальное и интегральное исчисление для втузов. Т. 1, 2. М.: Наука, 1970–1978; 1980; 1985; 1996. 7. Бермант А.Ф., Араманович И. Г. Краткий курс математического анализа. М.: Наука, 1966–1973; 2001; 2005. 8. Норкин С.В. и др. Элементы вычислительной математики. М.: Высшая школа, 1963–1966. 9. Кудрявцев В.А., Демидович Б.П. Курс высшей математики. М.: Наука, 1986–2011. 10. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. В 2 ч. М.: Финансы и статистика, 2001; 2011. 11. Кремер Н.Ш. Высшая математика для экономистов. М.: Наука, 2007. 12. Бугров Я.С., Никольский С.М. Высшая Математика. М.: Наука, 2004.
Далее для краткости названия книг обозначаются только их номером в приведенном здесь списке.
ТЕМА 1. Определители и системы Линейных уравнений. Матрицы
Литература: [1. Гл. VII]; [2. Гл. IV]; [4. Прил., § 1-6]; [9. Гл. XVII], [10. Ч. 1, Гл. II].
Вопросы для самопроверки
1. Что называется матрицей? 2. Что называется матрицей и расширенной матрицей линейных уравнений? 3. Что называется определителем и каковы его основные свойства? 4. Как вычисляются определитель 2-го и 3-го порядков? 5. Формулы Крамера. Когда они применимы? 6. В чем состоит сущность метода Гаусса? 7. Матрица и действия над матрицами.
ЗАДАЧА. Решить систему уравнений:
а) по методу Крамера, b) по методу Гаусса. Решение. а) Метод Крамера: Определитель 3-го порядка можно вычислить по правилу Саррюса:
Определитель 3-го порядка равен сумме произведений элементов вдоль ломанных на схеме с указанным знаком: плюс или минус.
Найдем определитель матрицы системы:
Вычислим вспомогательные определители:
Тогда
Проверка:
– верно. Ответ: б) Метод Гаусса. 1 этап.
1 шаг. Исключим неизвестное
Получим систему
или
2 шаг. Чтобы исключить неизвестное
Получим систему
или
2 этап. Из 3-го уравнения находим Ответ:
Векторы
Литература: [1. Гл. I, VIII]; [2. Гл. I, II]; [3. Гл. I-X]; [4. Гл. I-IV, VI, VII], [9. Гл. I-V, XVIII]
Вопросы для самопроверки
1. Расстояние между двумя точками и расстояние от точки до прямой. 2. Уравнения прямой линии. 3. Угол между двумя прямыми. 4. Условия параллельности и перпендикулярности прямых. 5. Угловой коэффициент прямой. 6. Что называется координатами вектора? 7. Действия над векторами. 8. Скалярное произведения двух векторов. 9. Векторное произведение двух векторов.
Даны вершины А (2; 5) В (-3; 1); С (0; 2) треугольника. Найти: 1) длину стороны ВС; 2) площадь треугольника (через векторы); 3) уравнение стороны ВС; 4) уравнение высоты, проведенной из вершины А; 5) длину высоты, проведенной из вершины А; 6) угол В в радианах с точностью до 0,01 (через векторы); 7) систему неравенств, определяющих треугольник АВС (рис. 1). Сделать чертеж.
Рисунок 1
Решение. 1) Определим длину стороны ВС по формуле
2) Найдем площадь треугольника АВС, где A (2; 5) В (-3; 1); С (0; 2). В трехмерном пространстве эти точки имеют координаты: A (2; 5; 0), В (-3; 1; 0); С (0; 2; 0).
Векторное произведение
где определитель вычислен по правилу Саррюса. Длина векторного произведения 3) Уравнение стороны ВС, проходящей через точки B (x 1, y 1), С (x 2, y 2), определим по формуле:
4) Уравнение высоты AD составим по формуле у – у 1 = k (x – x 1), где (x 1, y 1) – координаты точки А, k – угловой коэффициент высоты. Координаты точки А известны: А(2;5). Найдем k из условия перпендикулярности прямых Получили уравнение высоты 5) Длину высоты AD определим по следующей формуле:
6) Найдем угол В в радианах с точностью до 0,01. На плоскости векторы
7) Чтобы найти систему неравенств, определяющую треугольник АВС, необходимо составить уравнения всех трех сторон. Уравнение стороны ВС уже составлено: х -3 у + 6 = 0. Составим уравнения прямых АВ и АС:
Так как решением одного неравенства является полуплоскость (геометрически), то возьмем одну из точек этой полуплоскости и подставим в уравнение прямой, этим самым мы определим знак неравенства: Уравнение ВС: х -3 у + 6 = 0, для точки А (2; 5), 2-3×5 + 6 < 0; Уравнение АВ: Уравнение АС: Значит, решением неравенства х -3 у + 6 < 0 является та полуплоскость, в которой находится точка А; решением неравенства Итак, имеем
ТЕМА 3. Введение в анализ Литература: [1. Гл. II]; [2. Гл. V]; [6. Гл. I, II]; [9. Гл. VI-VIII]; [10, Ч. 2. Гл. I];
Вопросы для самопроверки
1. Функция. Область определения функции. 2. Предел переменной величины, предел функции. 3. Неопределенности видов 4. Как связано понятие предела функции с понятиями пределов слева и справа? 5. Непрерывность функции в точке и на отрезке. При вычислении пределов надо в первую очередь определить вид неопределенности. Для этого применяется метод подстановки: надо в функцию подставить число
Если в числителе и знаменателе стоят многочлены, Если в числителе и знаменателе стоят многочлены, Если Если получится неопределенность вида В последнем задании рекомендуется использовать 1-й замечательный предел:
ЗАДАЧИ Найти пределы функций. 1. 2. 3. 4.
5.
Таблица элементарных производных
1. 2. 3. 4.
5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19.
ЗАДАЧИ Найти производные заданных функций. a)
b)
c)
d)
e)
Для исследования функций Литература: [1. Гл. III,IV]; [7. Гл. IV]; [2. Гл. VII]; [6. Гл. IV]
Вопросы для самопроверки
1. Каковы признаки возрастания и убывания функции? 2. Что называется экстремумом функции? Как найти максимумы и минимумы функции? 3. Как находятся интервалы выпуклости и вогнутости и точки перегиба графика функции? 4. Что называется асимптотой к кривой? 5. Как находятся вертикальные и наклонные асимптоты графика функции? 6. Общая схема исследования функции и построения ее графика.
Схема исследования функции и построения графика. 1. Находим область определения функции и определяем, не ли у нее точек разрывов. Для каждого бесконечного разрыва учесть знак функции справа и слева. Получим вертикальные асимптоты. 2. Находим точки пересечения графика функции с осями координат. 3. Исследуем функцию на четность f(-x) = f(x) (график функции симметричен относительно оси ОУ) и нечетность f(-x) = -f(x) (график функции симметричен относительно начала координат) 4. Исследуем функцию на экстремум. Находим интервалы возрастания и убывания функции. 5. Исследуем функцию на точки перегиба. Находим интервалы выпуклости и вогнутости. 6. Определяем асимптоты. 7. Берем дополнительные точки (по необходимости). 8. Строим график.
ЗАДАЧА 1. Исследовать средствами дифференциального исчисления функцию Решение 1. Область определения функции (-¥; +¥), то есть функция определена на всей числовой оси. 2. Исследуем на четность f(-x) = f(x) или
Функция ни четная, ни нечетная. Это значит, что график не симметричен относительно осей координат. 3. Исследуем на экстремум:
Итак, точка максимума 4. Исследуем на точки перегиба:
Итак, точка
Найдем точки пересечения с осями. С осью OY: x = 0; Исследуем на асимптоты: данная функция вертикальных асимптот не имеет, так как она определена на всей числовой оси. Попытаемся найти наклонную асимптоту y = kx + b, где
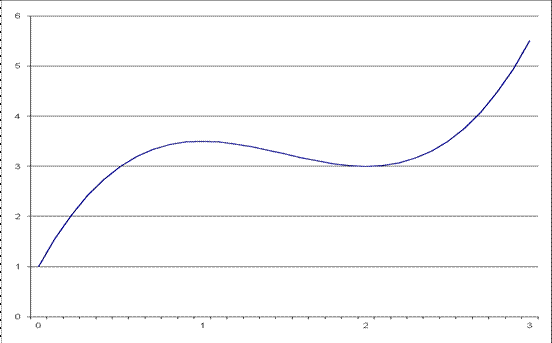
Следовательно, наклонных асимптот функция не имеет. Построим график. График функции показан на рис. 2.
Рисунок 2
ТЕМА 10. Двойной интеграл Литература: [1. Гл. XII]; [2. Гл. XIII]; [6. Гл. XIV]
Вопросы для самопроверки
1. Стандартная область 2. Правило вычисления двойного интеграла по стандартной области 1-го типа. 3. Стандартная область 4. Правило вычисления двойного интеграла по стандартной области 2-го типа. 5. Цилиндроид. 6. Связь двойного интеграла и объема цилиндроида. 7. Связь двойного интеграла и площади области
Область
Рисунок 3
Аналитически область D задается с помощью метода сечений:
Правило вычисления двойного интеграла от функции
где слева в (1) стоит двойной кратный интеграл, а справа – двойной повторный интеграл. В двойном повторном интеграле сначала вычисляется внутренний интеграл по y при фиксированном x, а потом – внешний по x. Аналогичным образом определяется стандартная область
ЗАДАЧА Вычислить двойной интеграл, если область D ограничена указанными линиями.
Решение. Область
Ответ:
ТЕМА 11. Ряды Литература: [1. Гл. XIII]; [2. Гл. XIV]; [6. Гл. XVI]
Вопросы для самопроверки
1. Что называется рядом? В каком случае ряд называется сходящимся, а в каком – расходящимся? Что называется суммой ряда? 2. Почему при исследовании сходимости ряда можно отбрасывать любое конечное число начальных членов? 3. Необходимый признак сходимости рядов. 4. Достаточные признаки сходимости рядов: признак Даламбера; Коши, интегральный, 2-й признак сравнения. 5. Знакочередующиеся ряды. Признак Лейбница. 6. Степенной ряд. Область сходимости и радиус сходимости степенного ряда Числовым рядом называется бесконечная сумма: Необходимый признак сходимости ряда. Если: 1) 2) Признак Даламбера. Если для
Признак Коши. Если для
Интегральный признак. Числовой ряд 2-й признак сравнения. Если для рядов Ряд Знакочередующий ряд: Признак Лейбница сходимости знакочередующего ряда. Если: 1) Степенной ряд Интервал сходимости степенного ряда ЗАДАЧИ 1) Исследовать сходимость числового ряда Решение. Так как
2) Исследовать сходимость числового ряда Решение. Так как
3) Исследовать сходимость числового ряда Решение. Исследуем ряд по интегральному признаку. Так как
4) Исследовать сходимость числового ряда Решение. Исследуем ряд по 2-му признаку сравнения. В качестве эталона рассмотрим похожий ряд
5) Найти область сходимости степенного ряда. Решение. Найдем параметры степенного ряда: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

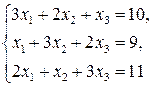
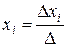 , где D – главный определитель системы; D хi вспомогательные определители.
, где D – главный определитель системы; D хi вспомогательные определители.
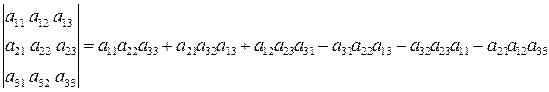

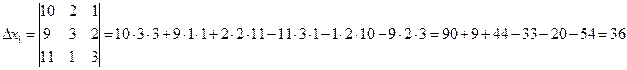


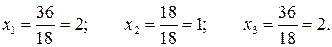
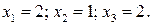
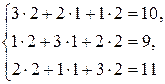
 из всех уравнений системы, начиная со второго. Чтобы исключить неизвестное
из всех уравнений системы, начиная со второго. Чтобы исключить неизвестное 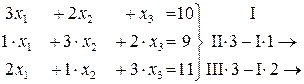
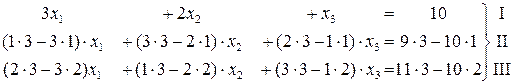

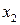 из 3-го уравнения, умножим 3-е уравнение на 7 и отнимем от полученного уравнения 2-е уравнение, умноженное на (-1).
из 3-го уравнения, умножим 3-е уравнение на 7 и отнимем от полученного уравнения 2-е уравнение, умноженное на (-1).
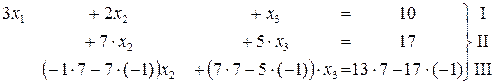

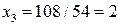 . Из 2-го уравнения находим
. Из 2-го уравнения находим 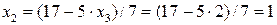 . Из 1-го уравнения находим
. Из 1-го уравнения находим 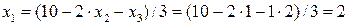 .
. ЗАДАЧА
ЗАДАЧА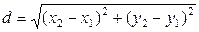
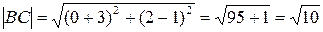 .
. Найдем координаты векторов
Найдем координаты векторов  и
и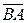 в трехмерном пространстве:
в трехмерном пространстве: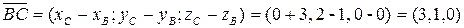 ,
,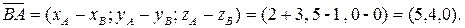
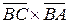 векторов
векторов 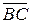 и
и  равно
равно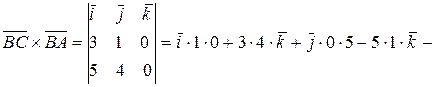
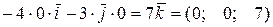 ,
,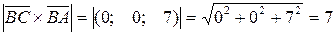 . Площадь треугольника равна
. Площадь треугольника равна  .
. , где x и y –координаты точки (x,y) на [ В,С ].
, где x и y –координаты точки (x,y) на [ В,С ].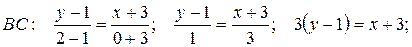 3 у – 3 = х +3, отсюда х -3 у + 6 = 0– общее уравнение стороны ВС.
3 у – 3 = х +3, отсюда х -3 у + 6 = 0– общее уравнение стороны ВС. . Сначала найдем kBC. Уравнение ВС: х -3 у + 6 = 0 приведем к виду BC:
. Сначала найдем kBC. Уравнение ВС: х -3 у + 6 = 0 приведем к виду BC: 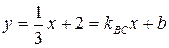 , откуда
, откуда  . Тогда
. Тогда 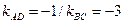 .
.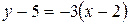 или 3 x + y – 11 = 0.
или 3 x + y – 11 = 0. , где (x 0, y 0) – координаты точки А;
, где (x 0, y 0) – координаты точки А;  – коэффициенты прямой ВС, расстояние до которой мы определяем.
– коэффициенты прямой ВС, расстояние до которой мы определяем. .
.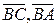 имеют координаты:
имеют координаты: 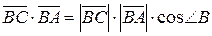 , таким образом,
, таким образом,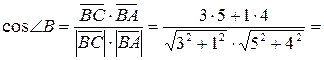
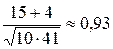 , отсюда ÐB = 0,93 радиан;
, отсюда ÐB = 0,93 радиан; – уравнение стороны АВ.
– уравнение стороны АВ.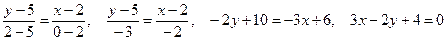 – уравнение стороны АС.
– уравнение стороны АС.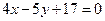 , для точки С (0; 2), -5×1 + 17 > 0;
, для точки С (0; 2), -5×1 + 17 > 0;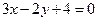 , для точки В (-3; 1), -3×3 - 2×1 + 4 < 0.
, для точки В (-3; 1), -3×3 - 2×1 + 4 < 0. является та полуплоскость, в которой находится точка С, и, наконец, решением неравенства
является та полуплоскость, в которой находится точка С, и, наконец, решением неравенства 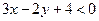 является та полуплоскость, в которой находится точка В, а пересечение всех этих полуплоскостей и определяет треугольник АВС.
является та полуплоскость, в которой находится точка В, а пересечение всех этих полуплоскостей и определяет треугольник АВС.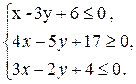
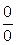 ,
, 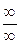 , 1¥ и их раскрытие
, 1¥ и их раскрытие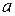 , к которому стремится переменная х:
, к которому стремится переменная х: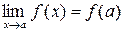 .
.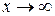 и получится неопределенность вида
и получится неопределенность вида  где
где 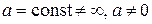 .
.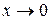 и получится неопределенность вида
и получится неопределенность вида 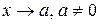 , получится неопределенность вида
, получится неопределенность вида 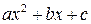 , то квадратные трехчлены разлагаются на множители с помощью формулы
, то квадратные трехчлены разлагаются на множители с помощью формулы 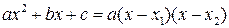 , где
, где 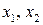 – корни квадратного уравнения
– корни квадратного уравнения  :
: 
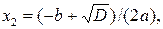
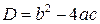 .
.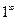 , то необходимо применить формулу 2-го замечательного предела:
, то необходимо применить формулу 2-го замечательного предела:  или
или 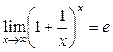 , где е» 2,71.
, где е» 2,71.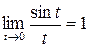 и четыре дополнительных предела:
и четыре дополнительных предела: 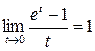 ,
,  ,
, 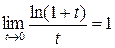 ,
, 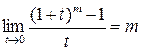 .
. так как
так как 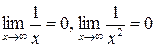 .
.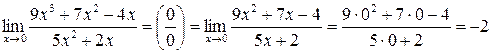 .
.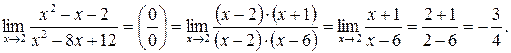

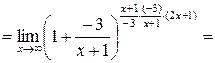
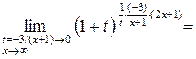
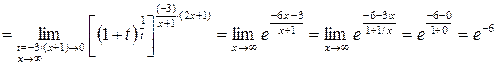 .
.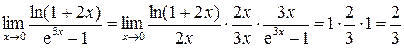 .
.
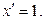
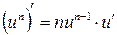

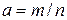





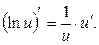
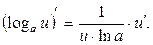

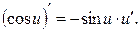
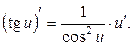


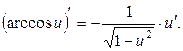

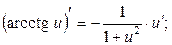
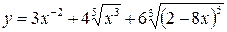 ,
,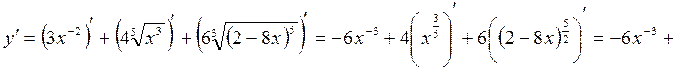
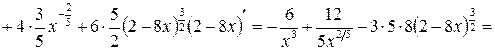
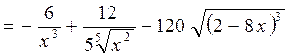 .
.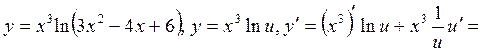
 .
.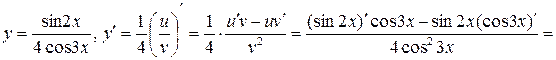
 .
.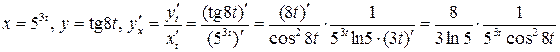 .
.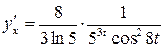 – производная параметрической функции.
– производная параметрической функции.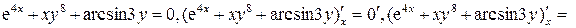
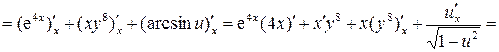
 ,
,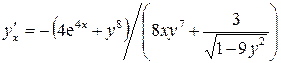 – производная неявной функции.
– производная неявной функции.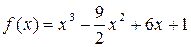 и построить ее график.
и построить ее график.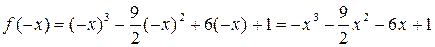 .
. – это точки, подозрительные на экстремум. Исследуем в таблице:
– это точки, подозрительные на экстремум. Исследуем в таблице: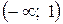
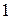
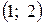





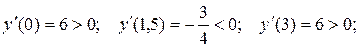
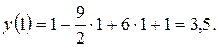

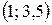 и точка минимума
и точка минимума  .
.

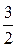





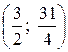 – точка перегиба.
– точка перегиба.
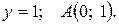
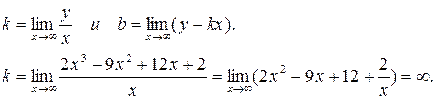

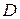 1-го типа в плоскости
1-го типа в плоскости  .
.
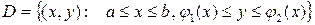 .
. по стандартной области D 1-го типа в плоскости
по стандартной области D 1-го типа в плоскости 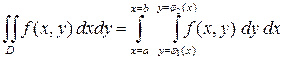 (1)
(1) для нее направлена вверх, а ось
для нее направлена вверх, а ось  направлена вправо.
направлена вправо. , D:
, D:  .
.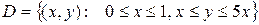 . По правилу вычисления двойного интеграла по стандартной области D 1-го типа в плоскости
. По правилу вычисления двойного интеграла по стандартной области D 1-го типа в плоскости 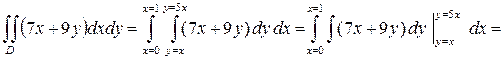

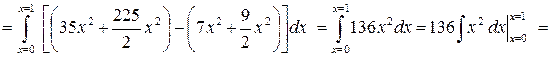

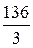 .
.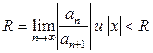 .
. , где
, где  – общий член ряда. Если бесконечная сумма существует и конечна, то говорят, что числовой ряд сходится, в противном случае – расходится.
– общий член ряда. Если бесконечная сумма существует и конечна, то говорят, что числовой ряд сходится, в противном случае – расходится.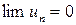 при
при 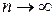 , то ряд может сходиться или расходиться;
, то ряд может сходиться или расходиться; при
при  существует предел:
существует предел: при
при 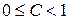 ряд сходится; при
ряд сходится; при  ряд расходится, при
ряд расходится, при 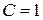 имеется неопределенность.
имеется неопределенность.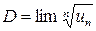 при
при 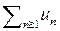 сходится или расходится одновременно с несобственным интегралом
сходится или расходится одновременно с несобственным интегралом 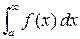 , где
, где  , число
, число 
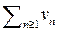 существует предел
существует предел 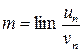 при
при 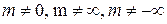 , то ряды сходятся или расходятся одновременно.
, то ряды сходятся или расходятся одновременно.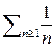 расходится; 2) обобщенный гармонический ряд
расходится; 2) обобщенный гармонический ряд  сходится при
сходится при 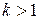 , расходится при
, расходится при 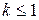 ; 3)
; 3) 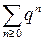 – бесконечная геометрическая прогрессия, при
– бесконечная геометрическая прогрессия, при 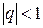 ряд сходится, при
ряд сходится, при  ряд расходится.
ряд расходится.
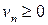 ; 2)
; 2)  монотонно убывают, то есть
монотонно убывают, то есть 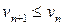 ; 3)
; 3) 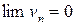 при
при  , где
, где 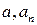 – коэффициенты степенного ряда.
– коэффициенты степенного ряда.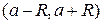 , где R – радиус сходимости степенного ряда можно находить по формуле Даламбера
, где R – радиус сходимости степенного ряда можно находить по формуле Даламбера  или по формуле Коши
или по формуле Коши  при
при  .
. содержит «n факториал» – произведение всех чисел от одного до n:
содержит «n факториал» – произведение всех чисел от одного до n:  , то сходимость ряда исследуется по признаку Даламбера. Заметим, что
, то сходимость ряда исследуется по признаку Даламбера. Заметим, что 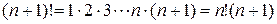 . Найдем
. Найдем 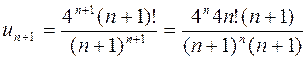 . По признаку Даламбера надо вычислить предел
. По признаку Даламбера надо вычислить предел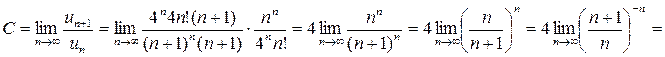
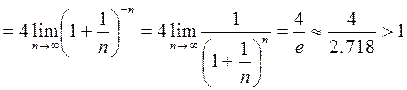 , так как по 2-му замечательному пределу
, так как по 2-му замечательному пределу 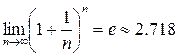 . Так как
. Так как  .
.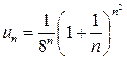 содержит только степени, то сходимость ряда исследуется по признаку Коши:
содержит только степени, то сходимость ряда исследуется по признаку Коши:
 . Так как
. Так как  , то ряд сходится.
, то ряд сходится. .
. , то
, то  . Числовой ряд
. Числовой ряд 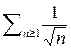 сходится или расходится одновременно с несобственным интегралом
сходится или расходится одновременно с несобственным интегралом  . Вычислим несобственный интеграл
. Вычислим несобственный интеграл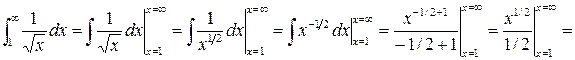
 – несобственный интеграл расходится. Следовательно, исходный числовой ряд расходится.
– несобственный интеграл расходится. Следовательно, исходный числовой ряд расходится. .
. – бесконечная геометрическая прогрессия, расходится. По 2-му признаку сравнения надо найти предел
– бесконечная геометрическая прогрессия, расходится. По 2-му признаку сравнения надо найти предел
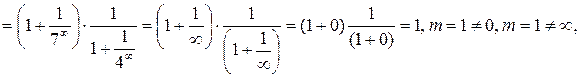
 , следовательно, ряды ведут себя одинаково. Так как эталонный ряд расходится, то исходный ряд тоже расходится.
, следовательно, ряды ведут себя одинаково. Так как эталонный ряд расходится, то исходный ряд тоже расходится. ,
,  . Радиус сходимости ряда вычислим по формуле Даламбера
. Радиус сходимости ряда вычислим по формуле Даламбера 


