
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел IV. Интегральное исчислениеСодержание книги
Поиск на нашем сайте
Раздел IV. Интегральное исчисление Глава 10. Неопределенный интеграл 10.1. Первообразная и неопределенный интеграл. Непосредственное интегрирование….2 10.2. Метод подстановки. Интегрирование по частям………………………………………3 10.3. Интегрирование рациональных функций. Разложение на простейшие дроби……...4 10.4. Интегрирование простейших дробей…………………………………………………..5. 10.5. Интегрирование тригонометрических функций………………………………………6 10.6. Интегрирование некоторых иррациональных функций………………………………7 Глава 11. Определенный интеграл 11.1.Понятие определенного интеграла и его свойства………………………………....8 11.2. Приближенное вычисление определенного интеграла. …………………………9 11.3. Интегрирование по частям и замена переменной в определенном интеграле....10 11.4. Несобственные интегралы с бесконечными пределами. ………………………..11 11.5. Несобственные интегралы от функций, имеющих разрыв. ……………………. 11.6. Вычисление площади плоской фигуры. …………………………………………. 11.7. Длина дуги кривой. ………………………………………………………………… 11.8. Вычисление объема и площади поверхности вращения………………………… Раздел V. Функции нескольких переменных Глава 12. Функции нескольких переменных Понятие функции нескольких переменных. Непрерывность функции нескольких переменных. Частные производные. Полный дифференциал функции нескольких переменных. Производная сложной функции. Дифференцирование функций заданных неявно. Частные производные и дифференциалы высших порядков. Экстремум функции нескольких переменных.
12.8. Производная по направлению. Градиент. Наибольшее и наименьшее значение функции нескольких переменных в замкнутой области. Условный экстремум функции нескольких переменных. Касательная плоскость и нормаль к поверхности. 12.12. Метод наименьших квадратов. Раздел IV. Интегральное исчисление Глава 10. Неопределенный интеграл Первообразная и неопределенный интеграл. Непосредственное интегрирование Основная задача дифференциального исчисления – отыскание производной заданной функции. Однако имеется обратная задача: по данной
Лемма: Функция, производная которой на некотором промежутке равна нулю, является константой.
Теорема. Если F (x) – первообразная для функции Доказательство. Пусть Ф (х) – другая первообразная, тогда Ф Для любого x: Определение. Если функция F (x) – первообразная для Восстановление функции по ее производной или отыскание неопределенного интеграла называется интегрированием. Свойства неопределённого интеграла:
Непосредственное интегрирование Вычисление интеграла путем использования таблиц и основных свойств называется непосредственным интегрированием. Примеры.
Метод подстановки. Интегрирование по частям Если известно, что Это вытекает из правила дифференцирования сложной функции. Примеры:
Интегрирование по частям Нет формулы, выражающий интеграл от произведения функций через интеграл от сомножителей. Интеграл от элементарной функции не всегда является элементарной функцией. Пусть имеются дифференцируемые функции u (х)и v (х): При использовании формулы интегрирования по частям необходимо выбрать функцию u, тогда оставшаяся часть будет дифференциалом функции v, т.е. dv. Можно указать следующие случаи: 1. В этом случае последовательное дифференцирование уменьшает показатель n до нуля. Наиболее простой случай, когда n = 1. 2. В этом случае дифференцирование указанных функций обычно упрощает нахождение интеграла. Примеры:
1)
Раздел II. Определенный интеграл Геометрические приложения определенного интеграла
Длина дуги кривой
а) Пусть кривая задана уравнением y = f (x). Возьмем на
L = Пример. Найти длину дуги кривой y = x3/2,
L =
б) Если кривая задана параметрически: L= в) Пусть кривая задана в полярных координатах:
тогда L = Пример. Найти длину дуги кардиоиды:
длина дуги:
Производная сложной функции Если z = f (u, v), а u и v являются функциями независимой переменной x: Если z = f (x, u, v), Пример:
Пример: Движение точки задано уравнениями:
Пусть z = f (u, v) и Пример.
Области Функция, ограниченная и дифференцируемая в замкнутой области, достигает в этой области своего наибольшего и наименьшего значения или во внутренних точек этой области (критических) или на её границе. Чтобы найти наибольшее и наименьшее значения функции в области D, надо найти все внутренние критические точки ( Пример: Найти наибольшее и наименьшее значение функции
(
г) Значения функции в вершинах треугольника: zнаиб=z (0,–5)=41; zнаимен = z (–2;–1)= –3. Метод наименьших квадратов Пусть известные значения некоторой функции f (x) образуют таблицу:
Требуется найти аналитическое выражение для этой функции. Можно применить метод интерполяции, однако совпадение значений в узлах может вовсе не означать совпадения характеров поведения исходной и интерполирующей функции. Поставим задачу следующим образом: найти функцию заданного вида y = F (x), которая в точках x 1, x 2, …, xn принимает значения как можно более близкие к табличным значениям y 1, y 2, …, yn. Следует заметить, что строгая функциональная зависимость для экспериментально полученной таблицы наблюдается редко, однако искомая формула (уравнение регрессии y на х) позволяет находить значения функции для не табличных значений х. Предположим, что приближающая функция F (x) в точках x 1, x 2, …, xn имеет значения В качестве приближающих функций в зависимости от вида функции f (х) часто используют функции: а) y = ax+b, б) y= ax2 + +bx + c, в) y = axm, г) y = aemx, д) y = 1 / (ax) + b, e) y = a Пусть необходимо определить три параметра, например, a, b, c, тогда искомая функциябудет является функцией этих параметров: F (xi, a, b, c). В обозначениях, принятых выше, F (xi, a, b, c) = =
Обозначим сумму квадратов разностей соответствующих значений функций f (x) и F (x) как U (a, b, c). Тогда получаем:
Решая эту систему трех уравнений с тремя неизвестными, определим значения параметров a, b, c и конкретный вид искомой функции F (x, a, b, c). Изменение количества параметров не приведёт к искажению сущности метода, а выразится лишь в изменении количества уравнений в системе. Рассмотрим подробнее линейную регрессию, т.е. будем искать приближающую функцию в виде: F (x, a, b) = ax + b. Частные производные по параметрам
Поскольку необходимо найти два параметра, то получили систему двух уравнений с двумя неизвестными. Преобразуем эту систему:
Это система двух линейных уравнений с двумя неизвестными (a, b). Решив ее, определяем параметры a и b:
Величины xi и yi – это значения из таблицы.
Понятие комплексного числа Комплексные числа – выражения вида Число a – действительная часть числа z, Сопряжённое число
Решение квадратного уравнения: ax 2 +bx+c=0, а 1) если D > 0, то 2 действительных корня: 2) если D=0 то 3) если D < 0, то 2 комплексных корня: Раздел IV. Интегральное исчисление
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 241; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.109.187 (0.011 с.) |

 найти F (x), производная которой равна
найти F (x), производная которой равна  по т. Лагранжа
по т. Лагранжа  ,
, 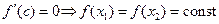 .
. (x) =
(x) =  , то есть
, то есть  .
. , где
, где  Табличные интегралы:
Табличные интегралы:


 .
.
 или, интегрируя, получим:
или, интегрируя, получим:  – формула интегрирования по частям.
– формула интегрирования по частям.
 .
.





 точки A, M 1, M 2 ,…Mi,…B, и проведем хорды, которые обозначим
точки A, M 1, M 2 ,…Mi,…B, и проведем хорды, которые обозначим  l 1,
l 1,  , вписанную в дугу АВ. Длина ломаной:
, вписанную в дугу АВ. Длина ломаной:  . Длина дуги – предел:
. Длина дуги – предел:  Если на отрезке [ a, b ] f (x),
Если на отрезке [ a, b ] f (x),  непрерывны, то этот предел существует. Пусть
непрерывны, то этот предел существует. Пусть  . По теореме Лагранжа
. По теореме Лагранжа  ,
,  , по условию, f(x) и
, по условию, f(x) и 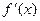 – непрерывны, поэтому существует предел интегральной суммы, который равен определенному интегралу:
– непрерывны, поэтому существует предел интегральной суммы, который равен определенному интегралу: =
=  .
.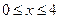 .
.


 то длина дуги
то длина дуги
 тогда
тогда 


 .
.
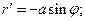
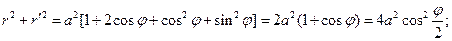

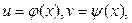 то и z является функцией x. Говорят, что z есть сложная функция аргумента x. Производная
то и z является функцией x. Говорят, что z есть сложная функция аргумента x. Производная  . (Аналогично для нескольких переменных).
. (Аналогично для нескольких переменных). то z – функция x и
то z – функция x и  .
.



 . С какой скоростью возрастает ее расстояние от начала координат?
. С какой скоростью возрастает ее расстояние от начала координат? Ищем
Ищем  ,
,  . Тогда получаем, что
. Тогда получаем, что
 . Пусть все функции имеют частные производные. Вычислим
. Пусть все функции имеют частные производные. Вычислим  и
и  . Дадим х приращение
. Дадим х приращение  разделим на
разделим на  и
и  .
.





 найти значения функции в этих точках, найти наибольшее и наименьшее значение функции на каждой линии, ограничивающей область D. Сравнить все полученные значения: наибольшее – max, наименьшее – min.
найти значения функции в этих точках, найти наибольшее и наименьшее значение функции на каждой линии, ограничивающей область D. Сравнить все полученные значения: наибольшее – max, наименьшее – min. в треугольнике, ограниченном осями координат и прямой x+у+ 5=0.
в треугольнике, ограниченном осями координат и прямой x+у+ 5=0.
 x = –2, у = –1.
x = –2, у = –1.  (–2;–1)= –3.
(–2;–1)= –3.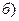 на оси ox: y=0, тогда z=x2 +3 x +1.
на оси ox: y=0, тогда z=x2 +3 x +1.





 . Тогда поставленная задача может быть сформулирована следующим образом: найти функцию заданного вида F (x) так, чтобы расстояние между точками М (y 1, y 2, …, yn) и
. Тогда поставленная задача может быть сформулирована следующим образом: найти функцию заданного вида F (x) так, чтобы расстояние между точками М (y 1, y 2, …, yn) и  было наименьшим, т.е. величина
было наименьшим, т.е. величина  была бы наименьшей, или сумма квадратов
была бы наименьшей, или сумма квадратов  должна принимать наименьшее значение.
должна принимать наименьшее значение.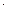 ln x + b, ж) y = a/x + b, з) y = x / (ax + b), где a, b, c, m – параметры, которые необходимо определить.
ln x + b, ж) y = a/x + b, з) y = x / (ax + b), где a, b, c, m – параметры, которые необходимо определить. , i = 1,2,…, n.
, i = 1,2,…, n. . Запишем необходимые условия экстремума:
. Запишем необходимые условия экстремума: 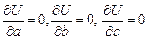 . Найдя частные производные, получаем систему:
. Найдя частные производные, получаем систему:
 . Составим систему уравнений (1):
. Составим систему уравнений (1):
 или
или  .
.

 , a,b – действительные числа, i – мнимая единица,
, a,b – действительные числа, i – мнимая единица,  . Числа
. Числа  действительные, 0 +bi – чисто мнимые.
действительные, 0 +bi – чисто мнимые. , b – мнимая часть числа z,
, b – мнимая часть числа z, 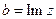 , модуль:
, модуль:  .
. (отличается знаком мнимой части). Два комплексных числа z 1 и z 2 равны, если a 1 = a 2; b 1 = b 2. Комплексное число равно 0, если a = 0, b = 0. С комплексными числами можно производить арифметические операции (по правилам алгебры):
(отличается знаком мнимой части). Два комплексных числа z 1 и z 2 равны, если a 1 = a 2; b 1 = b 2. Комплексное число равно 0, если a = 0, b = 0. С комплексными числами можно производить арифметические операции (по правилам алгебры): .
. .
. .
.
 =
=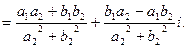
 0,
0, 
 ,
,
 .
.


