
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие функции нескольких переменныхСодержание книги
Поиск на нашем сайте
При рассмотрении многих явлений приходится иметь дело с функцией нескольких переменных. Например, площадь треугольника Переменные Будем вести изложение для функции двух переменных (n = 2), при этом практически все понятия и теоремы, сформулированные для n = 2, легко переносятся и на случай n > 2. Если каждой паре (x, y) значений двух независимых друг от друга переменных x и y из области D соответствует определенное значение величины z, то z – функция двух независимых переменных x, y: z = f (x, y). Функцию двух переменных можно задать с помощью формулы, аналитически или в виде таблиц (сложно). Совокупность пар (x, y) значений x и y, при которых определяется z = f(x, y), называется областью определения (существования) этой функции. Окрестностью Пример: Найти область определения функций: а) z = x + y, б) а) Вся плоскость xoy. б) Для функции Для функции Геометрически функция двух переменных определяет поверхность, которая проецируется на xoy в область определения функции. Линией уровня Z = f(x, y) называется множество точек на плоскости, для которых f (x, y) = С, где С – это уровень. Непрерывность функции нескольких переменных. Частные производные Число А называется пределом функции Функция Функция, непрерывная в каждой точке некоторой области D, называется непрерывной в этой области. Если условие (1) не выполняется, то точка (х 0; y 0) – точка разрыва. Если функция
Частные производные Пусть Полное приращение функции
Частной производной по y называется производная по y, вычисленная в предположении, что x = const: При определении частных производных сохраняются правила дифференцирования для функций одной переменной. Пример: Полный дифференциал функции нескольких переменных Пустьфункция
Полный дифференциал – главная линейная часть приращения функции: Пример:
Для функции трех переменных Пример:
Применение полного дифференциала в приближенных вычислениях Пусть Пример. Вычислить приближенно (1,03)3,001. Введем функцию
Производная сложной функции Если z = f (u, v), а u и v являются функциями независимой переменной x: Если z = f (x, u, v), Пример:
Пример: Движение точки задано уравнениями:
Пусть z = f (u, v) и Пример.
|
|||||
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 297; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.186.233 (0.009 с.) |

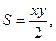 V = xyz – объем прямоугольного параллелепипеда и т.д. Пусть имеется n переменных величин и каждому набору их значений (
V = xyz – объем прямоугольного параллелепипеда и т.д. Пусть имеется n переменных величин и каждому набору их значений (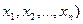 из некоторого множества Х соответствует одно определенное значение переменной величины z. Тогда говорят, что задана функция n переменных
из некоторого множества Х соответствует одно определенное значение переменной величины z. Тогда говорят, что задана функция n переменных  .
. – независимые переменные (аргументы), z – зависимая переменная – функция. Множество Х – область определения функции.
– независимые переменные (аргументы), z – зависимая переменная – функция. Множество Х – область определения функции. называется круг, содержащий точку
называется круг, содержащий точку  .
. ,
,  .
. – половина плоскости над прямой
– половина плоскости над прямой 
 при
при 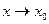 и
и  (в точке
(в точке  ), если для любого, сколь угодно малого
), если для любого, сколь угодно малого  найдется
найдется  такое, что для всех точек (x, y), отстоящих от точки
такое, что для всех точек (x, y), отстоящих от точки  на расстояние
на расстояние  меньшее, чем
меньшее, чем  (т.е. при
(т.е. при  ), выполняется неравенство
), выполняется неравенство 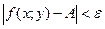 . Это обозначают так:
. Это обозначают так:  .
.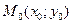 , если
, если  или
или  или
или 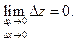 (1).
(1). , т.е. x = x +
, т.е. x = x +  x, тогда
x, тогда  называется частным приращением f (x, y) по переменной х, аналогично
называется частным приращением f (x, y) по переменной х, аналогично 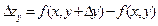 – называется частным приращением по y.
– называется частным приращением по y.
 т.к.
т.к. 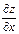 называется частной производной по х, вычисленной в предположении, что y = const.
называется частной производной по х, вычисленной в предположении, что y = const.

 (прибавили и вычли f (x, y +
(прибавили и вычли f (x, y + 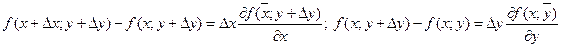 , где
, где 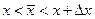 и
и 
 +
+ 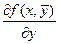 , т.к.
, т.к.  и
и 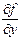 непрерывны, то
непрерывны, то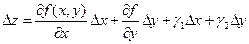 ,где
,где  – бесконечно малые величины при
– бесконечно малые величины при  и
и  ,
,  – полное приращение функции равно полному дифференциалу и бесконечно малым величинам высшего порядка малости.
– полное приращение функции равно полному дифференциалу и бесконечно малым величинам высшего порядка малости. (dx =
(dx =  ,
, 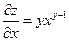 ,
, 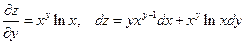 .
. полный дифференциал:
полный дифференциал:  .
.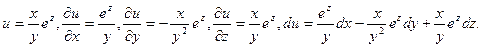

 но
но  при
при  , где
, где 

 ,
, 

 .
.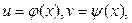 то и z является функцией x. Говорят, что z есть сложная функция аргумента x. Производная
то и z является функцией x. Говорят, что z есть сложная функция аргумента x. Производная  . (Аналогично для нескольких переменных).
. (Аналогично для нескольких переменных). то z – функция x и
то z – функция x и  .
.



 . С какой скоростью возрастает ее расстояние от начала координат?
. С какой скоростью возрастает ее расстояние от начала координат? Ищем
Ищем  ,
,  . Тогда получаем, что
. Тогда получаем, что
 . Пусть все функции имеют частные производные. Вычислим
. Пусть все функции имеют частные производные. Вычислим  и
и  . Дадим х приращение
. Дадим х приращение  разделим на
разделим на  и
и  .
.








