Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Несобственные интегралы с бесконечными пределамиСодержание книги
Поиск на нашем сайте
Пусть функция f (x)определена и непрерывна при всех Тогда несобственный интеграл Геометрический смысл: Аналогично, Для последнего равенства должны существовать оба интеграла, с – число. Пример 1. Исследовать на сходимость несобственный интеграл: y 0
Пример 2. При каких значениях параметра α интеграл α≠1; Пример 3.
Если требуется установить, сходится ли данный интеграл или расходится, удобно применять теоремы: 1. Если для всех 2. Если для всех 3. Если Пример 4. Сходится ли При Пример 5. Исследовать
Пример 6. Исследовать Подынтегральная функция знакопеременная.
Несобственные интегралы от функций, имеющих разрыв
Пусть функция f (x) определена и непрерывна при Интеграл Если функция имеет разрыв при х=а, то Если f (x) имеет разрыв в точке Пример 1. Исследовать сходимость
Пример 2. Геометрические приложения определенного интеграла
Вычисление площади плоской фигуры
а) Площадь плоской фигуры S =
Если f (x) <0 на интервале интегрирования, то рассматривают интеграл от модуля (или изменяют знак). S
Пример 1. Найти площадь фигуры, ограниченной графиком
Более удобной является формула: S =
y
Пример 2. Найти площадь, ограниченной параболой y = x 2 + 1 и прямой x + y =3
б) Пусть функция задана в параметрической форме:
Пример 3. Вычислить площадь одной арки циклоиды
x = 0, t = 0; x = 2
в) Если кривая задана в полярных координатах: Разобьем данную площадь радиус – векторами Пример 4. Найти S, ограниченную кардиоидой: Вычислить половину площади:
Длина дуги кривой
а) Пусть кривая задана уравнением y = f (x). Возьмем на L = Пример. Найти длину дуги кривой y = x3/2,
L =
б) Если кривая задана параметрически: L= в) Пусть кривая задана в полярных координатах:
тогда L = Пример. Найти длину дуги кардиоиды:
длина дуги:
Вычисление объема и площади поверхности вращения.
Пусть имеется тело, для которого известна площадь сечения, перпендикулярного оси ох, т.е. S = S (x). Проведем плоскости, перпендикулярные оси ох. Они разобьют тело на слои, Vслоя = =S (xi) Объем тела вращения:
Если ось вращения – ось O Y, то объем тела вращения: Vy = Если ось вращения – ось O X, то объем тела вращения: Площадь поверхности вращения.
Разобьем [ a, b ] на n частей и проведем ломаную. При вращении ломаной получаются усеченные конусы (цилиндры). Площадь поверхности Пример: Объем тела, образованного вращением вокруг оси ох фигуры, ограниченной линиями: 2 y = x2 и 2 x + 2 y – 3 = 0.
Раздел V. Функции нескольких переменных Глава 12. Функции нескольких переменных
|
|||||||
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.237.203 (0.006 с.) |

 .
. . Если предел существует, то интеграл существует или сходится, если предел не существует, то интеграл расходится (не существует), т.е. не имеет конечного значения.
. Если предел существует, то интеграл существует или сходится, если предел не существует, то интеграл расходится (не существует), т.е. не имеет конечного значения. выражает площадь бесконечной области, заключенной между линиями
выражает площадь бесконечной области, заключенной между линиями  .
.



 .
. сходится и при каких расходится?
сходится и при каких расходится? α=1;
α=1;  .
.

 выполняется неравенство
выполняется неравенство  и если
и если 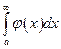 сходится, то
сходится, то  тоже сходится и
тоже сходится и  .
. причем
причем  расходится, то и
расходится, то и  расходится.
расходится. сходится, то и
сходится, то и  ?
? :
:  ,
,  , поэтому (т.1)
, поэтому (т.1)  .
. Но
Но  – расходится, поэтому рассматриваемый интеграл тоже расходится.
– расходится, поэтому рассматриваемый интеграл тоже расходится. на сходимость.
на сходимость. Но
Но 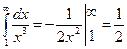 , значит, интеграл
, значит, интеграл  сходится, и по т.3 сходится и
сходится, и по т.3 сходится и  , а при x=b функция либо не определена, либо терпит разрыв. В этом случае нельзя говорить об
, а при x=b функция либо не определена, либо терпит разрыв. В этом случае нельзя говорить об 
 , как о пределе интегральной суммы, поскольку этот предел может не существовать.
, как о пределе интегральной суммы, поскольку этот предел может не существовать. Если предел существует, то интеграл сходится, иначе – расходится.
Если предел существует, то интеграл сходится, иначе – расходится. – аналогично, если предел существует, то интеграл сходится, иначе – расходится.
– аналогично, если предел существует, то интеграл сходится, иначе – расходится. внутри отрезка
внутри отрезка 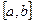 , то
, то  – существует, если существуют оба интеграла в правой части.
– существует, если существуют оба интеграла в правой части. .
. – сходится.
– сходится. – интеграл расходится.
– интеграл расходится. ,если
,если 


 или
или  .
.

 и осью абсцисс, если
и осью абсцисс, если 
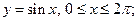

 .
. где
где  .
.
 f 2(x)
f 2(x)
 f 1(x)
f 1(x) 0 х
0 х
 (ед2)..
(ед2).. 


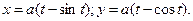

 a, t = 2
a, t = 2 


 M
M



 N
N




 0
0  x
x
 на n частей. Пусть углы между радиус – векторами равны
на n частей. Пусть углы между радиус – векторами равны  Площадь
Площадь  сектора
сектора 
 Площадь:
Площадь: 




 точки A, M 1, M 2 ,…Mi,…B, и проведем хорды, которые обозначим
точки A, M 1, M 2 ,…Mi,…B, и проведем хорды, которые обозначим  l 1,
l 1,  , вписанную в дугу АВ. Длина ломаной:
, вписанную в дугу АВ. Длина ломаной:  . Длина дуги – предел:
. Длина дуги – предел:  Если на отрезке [ a, b ] f (x),
Если на отрезке [ a, b ] f (x),  непрерывны, то этот предел существует. Пусть
непрерывны, то этот предел существует. Пусть  . По теореме Лагранжа
. По теореме Лагранжа  ,
,  , по условию, f(x) и
, по условию, f(x) и 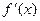 – непрерывны, поэтому существует предел интегральной суммы, который равен определенному интегралу:
– непрерывны, поэтому существует предел интегральной суммы, который равен определенному интегралу: =
=  .
.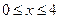 .
.


 то длина дуги
то длина дуги
 тогда
тогда 


 .
.
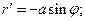
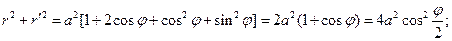


 Переходя к пределу:
Переходя к пределу:  V =
V = 

 .
.

 длина хорды
длина хорды 
 .
.