
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условный экстремум функции нескольких переменныхСодержание книги
Поиск на нашем сайте
Во многих задачах на отыскание наибольших и наименьших значений функции нескольких переменных эти переменные связаны друг с другом некоторым условием – это условный экстремум. Рассмотрим вопрос об условном экстремуме функции z=f (x,y) (1) при условии, что x и y связаны уравнением Если можно выразить y из (2) и подставить в (1), то получим функцию одного переменного x и далее очевидно. Введём функцию Лагранжа Вопрос о существовании и характере условного экстремума решается на основании изучения знака второго дифференциала функции Лагранжа Пример 1. Найти экстремум функции z= 6 – 4 x – 3 y при условии Функция Лагранжа:
Находим Пример 2. Выбрать из прямоугольных листов периметра 2p лист с наибольшей площадью. Пусть x,y – длина и ширина, тогда площадь u=xy, x и y связаны отношения: 2х+2у=2р, или
Касательная плоскость и нормаль к поверхности
Касательной плоскостью к поверхности в точке Нормалью к поверхности называется перпендикуляр к касательной плоскости в точке касания. Если уравнение поверхности
Пример. Найти уравнение касательной плоскости и нормали к поверхности
Метод наименьших квадратов Пусть известные значения некоторой функции f (x) образуют таблицу:
Требуется найти аналитическое выражение для этой функции.
Можно применить метод интерполяции, однако совпадение значений в узлах может вовсе не означать совпадения характеров поведения исходной и интерполирующей функции. Поставим задачу следующим образом: найти функцию заданного вида y = F (x), которая в точках x 1, x 2, …, xn принимает значения как можно более близкие к табличным значениям y 1, y 2, …, yn. Следует заметить, что строгая функциональная зависимость для экспериментально полученной таблицы наблюдается редко, однако искомая формула (уравнение регрессии y на х) позволяет находить значения функции для не табличных значений х. Предположим, что приближающая функция F (x) в точках x 1, x 2, …, xn имеет значения В качестве приближающих функций в зависимости от вида функции f (х) часто используют функции: а) y = ax+b, б) y= ax2 + +bx + c, в) y = axm, г) y = aemx, д) y = 1 / (ax) + b, e) y = a Пусть необходимо определить три параметра, например, a, b, c, тогда искомая функциябудет является функцией этих параметров: F (xi, a, b, c). В обозначениях, принятых выше, F (xi, a, b, c) = = Обозначим сумму квадратов разностей соответствующих значений функций f (x) и F (x) как U (a, b, c). Тогда получаем:
Решая эту систему трех уравнений с тремя неизвестными, определим значения параметров a, b, c и конкретный вид искомой функции F (x, a, b, c). Изменение количества параметров не приведёт к искажению сущности метода, а выразится лишь в изменении количества уравнений в системе. Рассмотрим подробнее линейную регрессию, т.е. будем искать приближающую функцию в виде: F (x, a, b) = ax + b. Частные производные по параметрам
Поскольку необходимо найти два параметра, то получили систему двух уравнений с двумя неизвестными. Преобразуем эту систему:
Это система двух линейных уравнений с двумя неизвестными (a, b). Решив ее, определяем параметры a и b:
Величины xi и yi – это значения из таблицы.
Понятие комплексного числа Комплексные числа – выражения вида Число a – действительная часть числа z, Сопряжённое число
Решение квадратного уравнения: ax 2 +bx+c=0, а 1) если D > 0, то 2 действительных корня: 2) если D=0 то 3) если D < 0, то 2 комплексных корня:
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 407; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.55.138 (0.006 с.) |

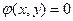 (2).
(2).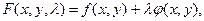 где
где  – коэффициент Лагранжа. Далее найдём частные производные функции
– коэффициент Лагранжа. Далее найдём частные производные функции 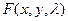 по x, y,
по x, y,  для найденных значений x, y,
для найденных значений x, y,  Функция f (x,y) имеет условный максимум, если
Функция f (x,y) имеет условный максимум, если 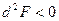 , и условный минимум, если
, и условный минимум, если  Если
Если  для F (x,y) положителен, то в этой точке условный максимум f (x,y), если A<0, и условный минимум, если A>0.
для F (x,y) положителен, то в этой точке условный максимум f (x,y), если A<0, и условный минимум, если A>0.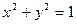 (сечение цилиндра плоскостью).
(сечение цилиндра плоскостью).
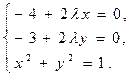
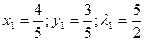 или
или 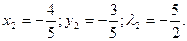
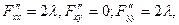 тогда
тогда 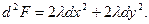 Если
Если 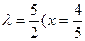 и
и 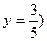 , то
, то 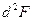 >0 и будет условный минимум
>0 и будет условный минимум 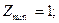 если
если  , то
, то 
 =x+y-p=0. Составим функцию:
=x+y-p=0. Составим функцию: 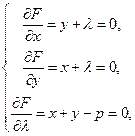
 .
. (точке касания) называется плоскость, в которой лежит все касательные в точке
(точке касания) называется плоскость, в которой лежит все касательные в точке  , то уравнение касательной плоскости в точке M 0(x 0, y 0, z 0):
, то уравнение касательной плоскости в точке M 0(x 0, y 0, z 0): 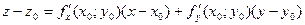 , уравнение нормали:
, уравнение нормали: 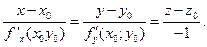 Если поверхность задана в виде F (x,y,z)=0, то
Если поверхность задана в виде F (x,y,z)=0, то 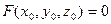
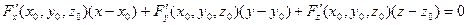 – уравнение касательной плоскости.
– уравнение касательной плоскости.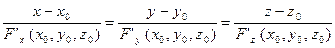 – уравнение нормали.
– уравнение нормали.
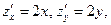 уравнение касательной плоскости:
уравнение касательной плоскости:  нормали:
нормали: 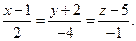
 . Тогда поставленная задача может быть сформулирована следующим образом: найти функцию заданного вида F (x) так, чтобы расстояние между точками М (y 1, y 2, …, yn) и
. Тогда поставленная задача может быть сформулирована следующим образом: найти функцию заданного вида F (x) так, чтобы расстояние между точками М (y 1, y 2, …, yn) и  было наименьшим, т.е. величина
было наименьшим, т.е. величина  была бы наименьшей, или сумма квадратов
была бы наименьшей, или сумма квадратов  должна принимать наименьшее значение.
должна принимать наименьшее значение.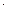 ln x + b, ж) y = a/x + b, з) y = x / (ax + b), где a, b, c, m – параметры, которые необходимо определить.
ln x + b, ж) y = a/x + b, з) y = x / (ax + b), где a, b, c, m – параметры, которые необходимо определить. , i = 1,2,…, n.
, i = 1,2,…, n. . Запишем необходимые условия экстремума:
. Запишем необходимые условия экстремума: 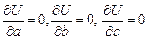 . Найдя частные производные, получаем систему:
. Найдя частные производные, получаем систему:
 . Составим систему уравнений (1):
. Составим систему уравнений (1):
 или
или  .
.

 , a,b – действительные числа, i – мнимая единица,
, a,b – действительные числа, i – мнимая единица,  . Числа
. Числа  действительные, 0 +bi – чисто мнимые.
действительные, 0 +bi – чисто мнимые. , b – мнимая часть числа z,
, b – мнимая часть числа z, 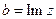 , модуль:
, модуль:  .
. (отличается знаком мнимой части). Два комплексных числа z 1 и z 2 равны, если a 1 = a 2; b 1 = b 2. Комплексное число равно 0, если a = 0, b = 0. С комплексными числами можно производить арифметические операции (по правилам алгебры):
(отличается знаком мнимой части). Два комплексных числа z 1 и z 2 равны, если a 1 = a 2; b 1 = b 2. Комплексное число равно 0, если a = 0, b = 0. С комплексными числами можно производить арифметические операции (по правилам алгебры): .
. .
. .
.
 =
=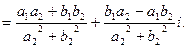
 0,
0, 
 ,
,
 .
.


