
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Циркуляция и поток векторного поляСодержание книги
Поиск на нашем сайте
Пусть Определение. Криволинейный интеграл
В обозначении криволинейного интеграла 2-го рода не указывается направление обхода контура, поэтому направление обхода контура надо указывать особо, причем положительным считается обход против часовой стрелки, а отрицательным – по часовой стрелке. Если контур
Из этого определения становится понятным физический смысл циркуляции векторного поля. А именно, если считать векторное поле Пусть Определение. Потоком векторного поля Физический смысл потока: если векторное поле Интегральные теоремы векторного анализа Теорема Гаусса – Остроградского. Поток векторного поля
Или в координатной форме:
Теорема Стокса. Циркуляция векторного поля Или в координатной форме:
Еще раз подчеркнем, что выбор стороны поверхности
Контрольная работа. Тема «Приложение кратных интегралов. Векторный анализ» Задания 1. Найти объём тела, ограниченного заданными поверхностями (таб. 1). 2. Найти угол между градиентами скалярных полей 3. Найти поток векторного поля 4. Найти циркуляцию векторного поля Пример выполнения контрольной работы. Вариант № 0 1. Найти объем тела, заданного ограничивающими его поверхностями.
Решение. Объем тела вычисляется по формулу:
Тело V ограничено снизу плоскостью Для вычисления интеграла удобно перейти к цилиндрическим координатам: Запишем уравнения границ в цилиндрических координатах: 1) 2)
Пределы изменения координат φ и ρ определяем по виду проекции области интегрирования V на плоскость xOy (Рис. 24). Пределы изменения угла φ будут от
Рис. 24 Таким образом,
Ответ: 2. Найти угол между градиентами скалярных полей Решение. Градиент скалярного поля
Находим частные производные функции
Аналогично, находим градиент поля
Напомним, что угол между векторами
Тогда:
Ответ: угол между градиентами скалярных полей 3. Найти поток векторного поля Решение. Если векторное поле
где V – тело, ограниченное замкнутой поверхностью S. Найдем дивергенцию поля, которая вычисляется по формуле:
В нашем случае имеем:
Тело V, границей которого является поверхность S, представляет собой треугольную пирамиду (Рис. 25) ограниченную координатными плоскостями и плоскостью
Рис. 25
Ответ: 4. Найти циркуляцию векторного поля Решение. Если линия задана параметрически, т. е.
В нашем случае
Подставляя эти выражения в формулу для вычисления циркуляции, получаем:
Ответ:
Варианты заданий контрольной работы Таблица 1. Варианты задания 1
Таблица 2. Варианты задания 2
Таблица 3. Варианты задания 3
Таблица 4. Варианты задания 4
Рекомендуемая литература 1. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа. М.: Наука,1960. 2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.2. М.: Высшая школа, 1980. 3. Краснов М.Л., Кисилев А.И., Макаренко Г.И. Векторный анализ. М.: Наука, 1978. 4. Лунгу К.Н., Норин В.П., Письменный Д.Т.,Шевченко Ю.А. Сборник задач по высшее математике. 2 курс. М.:Айрис-пресс, 2004. 5. Пискунов И.С. Дифференциальное и интегральное исчисления. Т. 2. М.: Наука, 1978. 6. Сборник задач по математике для ВТУЗов. Т. 2./под ред. Ефимова А.В., Демидовича Б.П., М.: Наука, 1981. 7. Фролов С.В., Шостак Р.Я. Курс высшей математики. Т. 2. М.: Наука, 1973.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 1687; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.008 с.) |

 - векторное поле, заданное в некоторой области
- векторное поле, заданное в некоторой области  , и функции
, и функции  - непрерывно дифференцируемы в области
- непрерывно дифференцируемы в области  . Пусть
. Пусть  - кусочно гладкая замкнутая кривая, расположенная в области
- кусочно гладкая замкнутая кривая, расположенная в области  называется циркуляцией векторного поля
называется циркуляцией векторного поля  (
( ) по контуру
) по контуру 
 , то есть
, то есть  - радиус-вектор точки кривой
- радиус-вектор точки кривой  и циркуляцию векторного поля по контуру
и циркуляцию векторного поля по контуру 
 - кусочно гладкая двусторонняя поверхность, на которой выбрана определенная сторона, задаваемая единичной нормалью
- кусочно гладкая двусторонняя поверхность, на которой выбрана определенная сторона, задаваемая единичной нормалью  к этой поверхности.
к этой поверхности. в направлении единичной нормали
в направлении единичной нормали  называется поверхностный интеграл первого рода:
называется поверхностный интеграл первого рода: 
 этого векторного поля через поверхность
этого векторного поля через поверхность  , ограниченному поверхностью
, ограниченному поверхностью 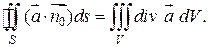


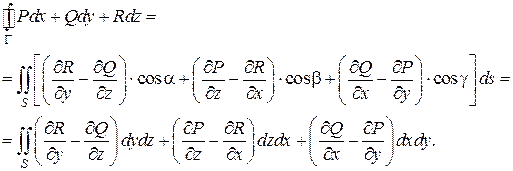
 и
и  в точке
в точке  (таб. 2).
(таб. 2). (нормаль внешняя) (таб. 3).
(нормаль внешняя) (таб. 3).

 , сверху параболическим цилиндром
, сверху параболическим цилиндром  , боковая поверхность - круговой цилиндр с центром в точке
, боковая поверхность - круговой цилиндр с центром в точке  и радиусом 1,
и радиусом 1,  .
. .
. ;
;
 .
.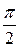 до
до  . При любом фиксированном угле φ, полярный радиус ρ изменяется от 0 до
. При любом фиксированном угле φ, полярный радиус ρ изменяется от 0 до  (уравнение окружности). При каждом значении (φ,ρ) в области D значение координаты z для области V меняются от
(уравнение окружности). При каждом значении (φ,ρ) в области D значение координаты z для области V меняются от  до
до  .
.



 .
. и
и  в точке
в точке  .
. в данной точке
в данной точке 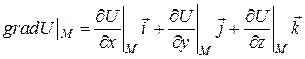 .
. :
: ,
,  ,
, 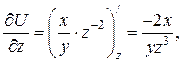
 ,
,  ,
,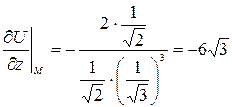 . Таким образом,
. Таким образом,  .
. в точке
в точке  ,
,  ,
,  .
.  ,
,  ,
, 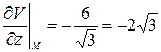 .
.  .
. и
и 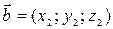 находится по формуле
находится по формуле .
. и
и  .
.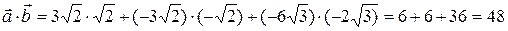 .
. .
. . Получаем:
. Получаем: 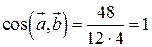 , то есть угол между градиентами равен нулю.
, то есть угол между градиентами равен нулю. и
и 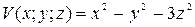 в точке
в точке  через внешнюю сторону замкнутой поверхности
через внешнюю сторону замкнутой поверхности  .
. непрерывно дифференцируемо внутри замкнутой поверхности
непрерывно дифференцируемо внутри замкнутой поверхности  ,
, .
. ;
;  ;
;  .
. ,
,  ,
,  . Следовательно,
. Следовательно,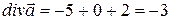 .
. (
( ).
).




 .
. вдоль замкнутого контура
вдоль замкнутого контура  (в направлении, соответствующем возрастанию параметра
(в направлении, соответствующем возрастанию параметра 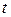 ).
). ,
,  , то циркуляция поля
, то циркуляция поля  равна:
равна:
 ,
, 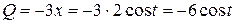 ,
,  .
. ,
,  ,
,  .
.
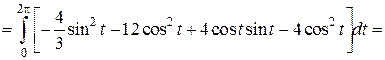




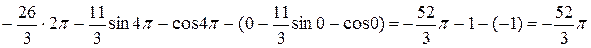 .
. .
. ,
,  ,
, 
 ,
, 
 ,
,  ,
,  ,
, 
 ,
, 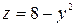 ,
,  ,
,  ,
,  ,
, 
 ,
, 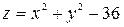 ,
,  ,
,  ,
, 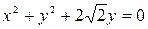 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 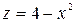 ,
,  ,
,  ,
,  ,
, 
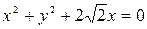 ,
,  ,
,  ,
,  ,
, 

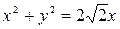 ,
,  ,
, 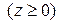
 ,
,  , z=0
, z=0
 ,
, 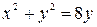 ,
, 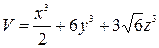 ,
,  ,
, 
 ,
,  ,
, 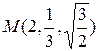
 ,
,  ,
, 
 ,
,  ,
, 
 ,
,  ,
,  ,
,  ,
, 
 ,
,  ,
, 
 ,
,  ,
, 
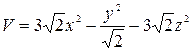 ,
,  ,
,  ,
,  ,
,  ,
, 
 ,
, 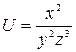 ,
, 
 ,
,  ,
, 
 ,
,  ,
, 
 ,
,  ,
, 
 ,
,  ,
, 
 ,
, 
 ,
,  ,
, 
 ,
,  ,
, 
 ,
,  ,
,  ,
,  ,
, 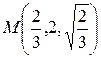
 ,
,  ,
, 
 ,
, 
 ,
,  ,
, 
 ,
,  ,
, 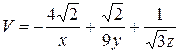 ,
,  ,
, 
 ,
,  ,
, 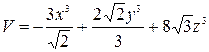 ,
, 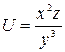 ,
, 
 - векторное поле (
- векторное поле ( - орты координатных осей),
- орты координатных осей),
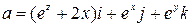 ,
,  ,
,  ,
,  ,
,  ,
,
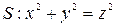 ,
,  ,
, 

 .
.
 ,
,  ,
, 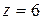
 ,
, 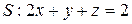 ,
,  ,
, 
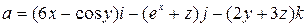 ,
, 
 ,
,

 ,
,  ,
, 
 ,
,
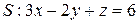 ,
,  ,
, 
 ,
,  ,
, 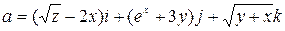 ,
,

 ,
,

 ,
,  ,
,  ,
,
 ,
, 
 ,
,
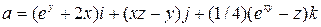 ,
,

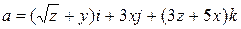 ,
,  ,
,  ,
,
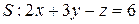 ,
,  ,
, 
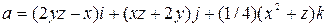 ,
,
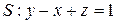 ,
,  ,
,
 ,
, 
 ,
,  ,
,
 ,
,  ,
,
 ,
, 
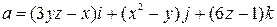 ,
,

 ,
,

 ,
,

 )
)


 ,
, 
 ,
, 
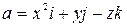 ,
, 

 ,
, 
 ,
, 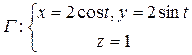
 ,
, 
 ,
, 
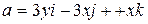 ,
, 
 ,
, 
 ,
, 
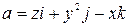 ,
, 
 ,
, 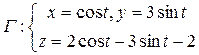
 ,
, 
 ,
, 
 ,
, 
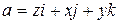 ,
, 
 ,
, 
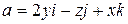 ,
, 
 ,
, 


 ,
, 
 ,
,  ,
, 

 ,
, 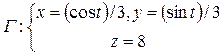
 ,
, 
 ,
, 
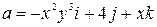 ,
, 



