
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрический и физический смысл двойного интеграла. Основные свойства двойного интеграла.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Геометрический и физический смысл двойного интеграла. Основные свойства двойного интеграла. Геометрический смысл двойного интеграла. Двойной интеграл от неотрицательной функции (
Физический смысл двойного интеграла. Двойной интеграл от функции
Основные свойства двойного интеграла Свойства двойного интеграла аналогичны свойствам определенного интеграла функции одной переменной на отрезке. Поэтому перечислим основные свойства двойного интеграла (без доказательства), считая подынтегральные функции интегрируемыми. 1.
2.
3. Если область
4. Если в области
5. Если в области
6. Если
7. Если функция
где
8. Если функция
Величину 3. Вычисление двойного интеграла в декартовых координатах. Вычисление двойного интеграла В декартовых координатах Покажем, что вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов. Пусть требуется вычислить двойной интеграл
направлении оси Построим сечение цилиндрического тела плоскостью, перпендикулярной оси В сечении получаем криволинейную трапецию
Теперь, согласно методу параллельных сечений, искомый объем цилиндрического тела может быть найден так:
С другой стороны, объем цилиндрического тела определяется как двойной интеграл от функции
Таким образом, для вычисления двойного интеграла функции
Правую часть (1.2) называют двукратным (или повторным) интегралом от функции Для вычисления двукратного интеграла сначала берем внутренний интеграл, считая Если область
В полярных координатах При вычислении определенного интеграла важную роль играет правило замены переменной, согласно которому при соблюдении соответствующих условий получаем
Обычно функция Для упрощенного вычисления двойного интеграла также применяется метод подстановки. Но правило замены переменной в двойном интеграле значительно сложнее, чем в определенном интеграле. Приведем только окончательную формулу замены переменных в двойном интеграле и разъясним ее на примере преобразования к полярным координатам.
Определим преобразование независимых переменных
Если функции
а функция
Сами новые переменные Функциональный определитель Рассмотрим частный случай замены переменных, часто используемый при вычислении двойного интеграла, а именно замену декартовых координат В качестве переменных Правые части в этих равенствах – непрерывно дифференцируемые функции. Якобиан преобразования определяется как
Формула замены переменных (1.4) принимает вид:
где 5. Приложения двойного интеграла в геометрии и физике. Объем такого цилиндра численно равен площади основания 1. для вычисления в декартовой системе координат: 2. для вычисления в полярной системе координат: Масса плоской фигуры
Согласно физическому смыслу двойного интеграла, масса плоской пластины находится по формуле:
где
Координаты центра масс
Координаты плоской фигуры
В сферических координатах В некоторых случаях вычисление тройного интеграла удобно производить, перейдя к сферическим координатам. Сферическими координатами точки
Возьмем в качестве
Формула замены переменных (1.9) принимает вид:
Переходить к сферическим координатам удобно, когда область интегрирования Объем тела
Объем тела 1. 2. 3.
Масса тела
Масса тела
Статистические моменты
Статистические моменты
Координаты центра масс
Координаты центра тяжести тела
Моменты инерции тела
Моменты инерции тела относительно координатных плоскостей вычисляются по формулам:
Моменты инерции тела относительно осей координат:
Основные свойства КРИ-I
1. 2. 3. 4. 5. Если для точек кривой
6. Если 7. (Теорема о среднем) Если функция Явное представление кривой Если кривая
Площадь плоской фигуры Площадь
при этом кривая Работа переменной силы Переменная сила
Градиент В каждой точке области Градиентом функции
Подчеркнем, что проекции градиента зависят от выбора точки Используя определение градиента, формуле для производной по направлению можно придать следующий вид:
где j - угол между Формула Стокса Рассмотрим в пространстве кусок двухсторонней кусочно-гладкой поверхности Эту же формулу Стокса можно записать и векторной форме:
Формула (4.15) означает следующее: циркуляция векторного поля Формула Стокса Рассмотрим в пространстве кусок двухсторонней кусочно-гладкой поверхности Эту же формулу Стокса можно записать и векторной форме:
Формула (4.15) означает следующее: циркуляция векторного поля Признак Даламбера В отличие от признаков сравнения, где все зависит от догадки и запаса известных сходящихся и расходящихся рядов, признак Даламбера (1717 – 1783, французский математик) позволяет часто решать вопрос о сходимости ряда, проделав лишь некоторые операции над самими рядами. Теорема 1.5 (признак Даламбера). Пусть дан ряд (1.1) с положительными членами и существует конечный или бесконечный предел
Тогда: 1) при 2) при При Признак Даламбера целесообразно применять, когда общий член ряда содержит выражения вида Вычисление значений функции Пусть дан степенной ряд функции Вычисление интегралов Так как степенные ряды сходятся равномерно на любом отрезке, лежащем внутри интервалов сходимости, то с помощью разложений функций в степенные ряды можно находить неопределенные интегралы в виде степенных рядов и приближенно вычислять соответствующие определенные интегралы. Геометрический и физический смысл двойного интеграла. Основные свойства двойного интеграла. Геометрический смысл двойного интеграла. Двойной интеграл от неотрицательной функции (
Физический смысл двойного интеграла. Двойной интеграл от функции
Основные свойства двойного интеграла Свойства двойного интеграла аналогичны свойствам определенного интеграла функции одной переменной на отрезке. Поэтому перечислим основные свойства двойного интеграла (без доказательства), считая подынтегральные функции интегрируемыми. 1.
2.
3. Если область
4. Если в области
5. Если в области
6. Если
7. Если функция
где
8. Если функция
Величину 3. Вычисление двойного интеграла в декартовых координатах.
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 12688; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.152.168 (0.008 с.) |

 ) численно равен объему тела, которое сверху ограничено поверхностью
) численно равен объему тела, которое сверху ограничено поверхностью  , снизу – замкнутой областью
, снизу – замкнутой областью  плоскости
плоскости  , с боков – цилиндрической поверхностью, образующая которой параллельна оси
, с боков – цилиндрической поверхностью, образующая которой параллельна оси  , а направляющей служит граница
, а направляющей служит граница  .
. численно равен массе плоской пластины, если подынтегральная функция
численно равен массе плоской пластины, если подынтегральная функция 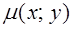 считать плотностью этой пластины в точке
считать плотностью этой пластины в точке  , т.е.
, т.е.
 , где
, где  .
. .
. разбить линией на две области
разбить линией на две области  и
и  такие, что
такие, что  , а пересечение
, а пересечение  , где
, где  - линия, разделяющая
- линия, разделяющая 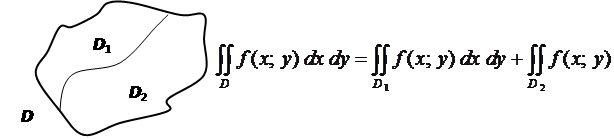
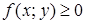 , то и
, то и .
. функции
функции  и
и  удовлетворяют неравенству
удовлетворяют неравенству  , то и
, то и .
. ,
,  , то
, то  , где
, где  - площадь области интегрирования
- площадь области интегрирования  непрерывна в замкнутой области
непрерывна в замкнутой области  , то
, то ,
, и
и  - соответственно наименьшее и наибольшее значения подынтегральной функции в области
- соответственно наименьшее и наибольшее значения подынтегральной функции в области  непрерывна в замкнутой области
непрерывна в замкнутой области  , что
, что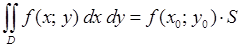 .
. называют средним значением функции
называют средним значением функции  , где функция
, где функция  непрерывна в области
непрерывна в области  . Найдем этот объем, используя метод параллельных сечений. Ранее было показано, что
. Найдем этот объем, используя метод параллельных сечений. Ранее было показано, что  , где
, где  - площадь сечения плоскостью, перпендикулярной оси
- площадь сечения плоскостью, перпендикулярной оси  , а
, а  и
и  - уравнения плоскостей, ограничивающих данное тело.
- уравнения плоскостей, ограничивающих данное тело.
 : любая прямая, параллельная оси
: любая прямая, параллельная оси  , где
, где  .
. , ограниченную линиями
, ограниченную линиями  и
и  . Площадь
. Площадь  этой трапеции находим с помощью определенного интеграла:
этой трапеции находим с помощью определенного интеграла: .
. .
. .
. по области
по области  (1.2)
(1.2) . Интеграл
. Интеграл  называется внутренним интегралом.
называется внутренним интегралом. постоянным, затем берем внешний интеграл, т.е. результат первого интегрирования интегрируем по
постоянным, затем берем внешний интеграл, т.е. результат первого интегрирования интегрируем по  в пределах от
в пределах от  до
до  .
. ограничена прямыми
ограничена прямыми  и
и  (
( ), кривыми
), кривыми  и
и 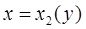 , причем
, причем  для всех
для всех  , т.е. область
, т.е. область  , аналогично получаем
, аналогично получаем
 .
. монотонна. Она осуществляет взаимно однозначное соответствие между точками промежутка
монотонна. Она осуществляет взаимно однозначное соответствие между точками промежутка  изменения переменной
изменения переменной  и точками промежутка
и точками промежутка  изменения переменной
изменения переменной  . Делая замену по формуле
. Делая замену по формуле  , необходимо
, необходимо  заменить на
заменить на  и вместо старых пределов
и вместо старых пределов  и
и 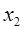 по переменной
по переменной  и
и  по переменной
по переменной  .
. как
как и
и  .
. и
и  имеют в некоторой области
имеют в некоторой области  плоскости
плоскости  непрерывные частные производные первого порядка и отличный от нуля определитель
непрерывные частные производные первого порядка и отличный от нуля определитель ,
, непрерывна в области
непрерывна в области  . (1.4)
. (1.4) и
и  называются криволинейными координатами. Различные системы криволинейных координат играют важную роль в математике и ее приложениях.
называются криволинейными координатами. Различные системы криволинейных координат играют важную роль в математике и ее приложениях. называется определителем Якоби или якобианом (Г. Якоби (1804 – 1851) – немецкий математик).
называется определителем Якоби или якобианом (Г. Якоби (1804 – 1851) – немецкий математик). и
и  .
. ,
,  .
.
 , (1.5)
, (1.5) , т.е. площади области интегрирования
, т.е. площади области интегрирования  ;
; .
. ,
, - плотность этой пластины.
- плотность этой пластины.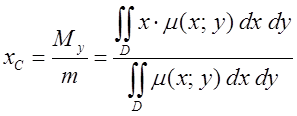 ;
; .
. пространства
пространства  называется тройка чисел
называется тройка чисел  , где
, где  на плоскость
на плоскость  и осью
и осью  ,
,  - угол отклонения радиус-вектора
- угол отклонения радиус-вектора  (см. рис.).
(см. рис.).
 сферические координаты
сферические координаты  и вычислим якобиан преобразования:
и вычислим якобиан преобразования: .
. . (1.11)
. (1.11) есть шар (равнение его границы
есть шар (равнение его границы  в сферических координатах имеет вид
в сферических координатах имеет вид  ) или его часть, а также, если подынтегральная функция имеет вид
) или его часть, а также, если подынтегральная функция имеет вид  .
. выражается следующими формулами:
выражается следующими формулами: - в декартовых координатах;
- в декартовых координатах; - в цилиндрических;
- в цилиндрических; - в сферических координатах;
- в сферических координатах; в точке
в точке  вычисляется с помощью тройного интеграла по следующей формуле
вычисляется с помощью тройного интеграла по следующей формуле
 ,
,  ,
,  тела относительно координатных плоскостей
тела относительно координатных плоскостей  ,
,  ,
,  вычисляются по формулам:
вычисляются по формулам: ;
;
 .
. ,
,  ,
,  .
. ;
;
 .
. ;
;
 .
. , т.е. криволинейный интеграл I рода не зависит от направления пути интегрирования.
, т.е. криволинейный интеграл I рода не зависит от направления пути интегрирования. , где
, где  .
. .
. , если путь интегрирования
, если путь интегрирования  разбить на части
разбить на части  и
и  такие, что
такие, что  ,
,  , то
, то .
. , то
, то  , где
, где  - длина кривой
- длина кривой  (геометрический смысл криволинейного интеграла первого рода).
(геометрический смысл криволинейного интеграла первого рода). непрерывная на кривой
непрерывная на кривой  , то на этой кривой найдется точка
, то на этой кривой найдется точка  , что
, что  .
. лежит в плоскости
лежит в плоскости  и задана уравнением
и задана уравнением  , производная
, производная  непрерывна на
непрерывна на  ,
,  , то
, то .
. плоской фигуры, расположенной в плоскости
плоской фигуры, расположенной в плоскости  и ограниченной замкнутой линией
и ограниченной замкнутой линией  ,
, на криволинейном участке
на криволинейном участке 
 , в которой задана скалярная функция
, в которой задана скалярная функция  , определим вектор, проекциями которого на оси координат являются значения частных производных
, определим вектор, проекциями которого на оси координат являются значения частных производных  в выбранной точке
в выбранной точке  . Назовем этот вектор градиентом функции
. Назовем этот вектор градиентом функции 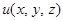 и обозначим его символами
и обозначим его символами 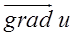 или
или 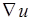 (набла-оператор, записываемый в виде «вектора» с компонентами
(набла-оператор, записываемый в виде «вектора» с компонентами 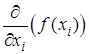 ).
).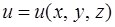 в точке
в точке 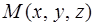 называется вектор, проекции которого служат значения частных производных этой функции, т.е.
называется вектор, проекции которого служат значения частных производных этой функции, т.е. . (4.3)
. (4.3)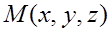 и изменяются с изменением координат этой точки. Таким образом, каждой точке скалярного поля, определяемого функцией
и изменяются с изменением координат этой точки. Таким образом, каждой точке скалярного поля, определяемого функцией 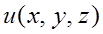 , соответствует определенный вектор – градиент этой функции. Отметим, что градиент линейной функции
, соответствует определенный вектор – градиент этой функции. Отметим, что градиент линейной функции  есть постоянный вектор
есть постоянный вектор  .
. ,которая читается так: производная функции по данному направлению равна скалярному произведению градиента функции на единичный вектор этого направления (
,которая читается так: производная функции по данному направлению равна скалярному произведению градиента функции на единичный вектор этого направления ( ).Учитывая то, что скалярное произведение равно модулю одного вектора умноженному на проекцию другого вектора на направление первого, то можно еще сказать, что: производная функции по данному направлению равна проекции градиента функции на направление дифференцирования, т.е.
).Учитывая то, что скалярное произведение равно модулю одного вектора умноженному на проекцию другого вектора на направление первого, то можно еще сказать, что: производная функции по данному направлению равна проекции градиента функции на направление дифференцирования, т.е.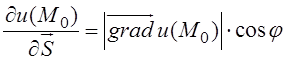 ,
, и направлением
и направлением 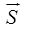 .
. , край которой образуется кусочно-гладкой кривой
, край которой образуется кусочно-гладкой кривой  . Выберем положительную сторону поверхности (из конца единичного вектора нормали
. Выберем положительную сторону поверхности (из конца единичного вектора нормали  обход границы представляется против часовой стрелки). Для циркуляции векторного поля
обход границы представляется против часовой стрелки). Для циркуляции векторного поля  вдоль контура границы имеет место формула Стокса:
вдоль контура границы имеет место формула Стокса: 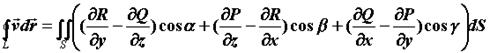 , где
, где  - компоненты векторного поля,
- компоненты векторного поля,  - направляющие косинусы вектора нормали.
- направляющие косинусы вектора нормали. . (4.15)
. (4.15)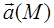 вдоль замкнутого контура
вдоль замкнутого контура  равна потоку ротора этого поля через любую гладкую поверхность
равна потоку ротора этого поля через любую гладкую поверхность  , краем которой является контур
, краем которой является контур  . Направление обхода по контуру
. Направление обхода по контуру  и сторона поверхности
и сторона поверхности  одновременно или положительные, или отрицательные.
одновременно или положительные, или отрицательные. , где
, где  .
. ряд сходится;
ряд сходится; ряд расходится.
ряд расходится. признак Даламбера не дает ответа на вопрос о сходимости или расходимости ряда. В этом случае сходимость ряда исследуется с помощью других признаков.
признак Даламбера не дает ответа на вопрос о сходимости или расходимости ряда. В этом случае сходимость ряда исследуется с помощью других признаков. или
или  .
. . Задача вычисления значения этой функции заключается в отыскании суммы ряда при заданном значении аргумента. Ограничиваясь определенным числом членов ряда, находим значение функции с точностью, которую можно устанавливать путем оценивания остатка числового ряда либо остаточного члена
. Задача вычисления значения этой функции заключается в отыскании суммы ряда при заданном значении аргумента. Ограничиваясь определенным числом членов ряда, находим значение функции с точностью, которую можно устанавливать путем оценивания остатка числового ряда либо остаточного члена  формул Тейлора или Маклорена.
формул Тейлора или Маклорена.


