
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства арифметического корняСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если a и b — неотрицательные числа, n и k — натуральные числа, отличные от единицы, m — целое число, то имеют место следующие соотношения:
Степень с дробным показателем Если a — положительное число, m — целое число, n — натуральное число и n ≥ 2, то Формулы сокращенного умножения
Дробно−рациональные уравнения Свойства рациональных дробей:
Логарифмические уравнения Логарифмы Логарифмом числа b по основанию а (logₐb) называют такое число с, что b = aᶜ, т.е. записи logₐb = c и b = aᶜ равносильны. Логарифм имеет смысл, если a > 0, a ≠ 1, b > 0. Если немного перефразировать — логарифм числа b по основанию a определяется как показатель степени, в которую надо возвести число a, чтобы получить число b (логарифм существует только у положительных чисел). Специальные обозначения: Натуральный логарифм ln a — логарифм по основанию e, где e — число Эйлера. Десятичный логарифм lg a — логарифм по основанию 10. Свойства логарифмов: 1. 2. logₐ a = 1, a > logₐ a = 1, a > 0, a ≠ 1. 3. logₐ1 = 0, a > 0, a ≠ 1. Логарифм единицы по любому положительному, отличному от 1, основанию равен нулю. Это возможно потому, что из любого действительного числа можно получить 1 только возведя его в нулевую степень. 4. log a (bc) = log ab + log ac — логарифм произведения. Логарифм произведения равен сумме логарифмов сомножителей. 5. log Логарифм частного (дроби) равен разности логарифмов сомножителей. 6. log abp = p · log ab — логарифм степени. Логарифм степени равен произведению показателя степени на логарифм ее основания. 7. 8. log ab = 9. log ab = 10. 11. log ax 2 k = 2 k log a ǀ x ǀ (a ≠ 1, a > 0, k ϵ R, x ≠ 0). Основное логарифмическое тождество Показательное уравнение aˣ = b, a > 0, a ≠ 1 не имеет решений при b ≤ 0 и имеет единственный корень в случае, когда b > 0. Этот корень называют логарифмом числа b по основанию a и обозначают log ab, то есть
Выражение Логарифмическая функция Функцию, которую можно записать формулой y = logₐ x, называют логарифмическойфункцией. Здесь x > 0 — аргумент, a > 0, a ≠ 1 — основание логарифма. Свойства логарифмической функции: 1. Область определения: D (y); x є (0; +∞); 2. Область значений: E (y): y є (−∞; +∞); 3. Функция ни четная, ни нечетная; 4. Нули функции: x = 1; 5. График функции возрастает на (0; +∞) при a > 1; убывает на (0; +∞) при 0 < a < 1; точек экстремума нет; 6. График логарифмической функции:
Логарифмические уравнения Логарифмическое уравнение — это такое уравнение, в котором неизвестная стоит под знаком логарифма. При решении логарифмических уравнений часто приходится логарифмировать или потенцировать обе части уравнения, что не всегда может привести к равносильным уравнениям. Логарифмировать алгебраическое выражение — значит выразить его логарифм через логарифмы отдельных чисел, входящих в это выражение. Пример: прологарифмировать выражение x = 3 bc. Решение. В левой и правой части допишем логарифм по основанию a: log ax = log a (3 bc). По свойствам логарифмов логарифм произведения, стоящий в правой части, представим как сумму логарифмов от каждого из сомножителей, то есть: logₐ x = logₐ3 + logₐ b + logₐ c. Определение: если по данному результату логарифмирования находят выражение, от которого получен этот результат, то такая операция называется потенцированием. Пример: пропотенцировать выражение: log ax = 5log ac − log ad. Решение. Используя свойства логарифмов, преобразуем правую часть данного выражения: 5log ac – log ac 5 – log ad = log a 5log ac – log ad = log ac 5 − log ad = log a log ax = log a x = 1. Простейшим логарифмическим уравнением является уравнение logₐ x = b причем основание логарифма a > 0, a ≠ 1, а под логарифмическое выражение x > 0. Для любого действительного b это уравнение имеет единственное решение x = ab. Пример: решить уравнение: log5 x = 2. Решение. Вначале находим область допустимых значений (ОДЗ): x > 0, тогда единственное решение уравнения x = 52 = 25.
Ответ:x = 25. 2. Логарифмическое уравнение вида log af (x) = b. Здесь a > 0, a ≠ 1, — элементарная алгебраическая функция, причем, чтобы уравнение имело решение, должно выполняться неравенство f (x) > 0 Заменой f (x) = t данное уравнение приводится к простейшему логарифмическому уравнению logₐ t = b, решение которого приведено в пункте 1. Пример: решить уравнение: log2(x 2 + 4) = 3. Решение. ОДЗ: x ² + 4 > 0 Замена: x ² + 4 = t, получаем уравнение log2 t = 3, решение которого t = 2³ = 8. Делаем обратную замену, получаем: x ² + 4 = 8 Ответ: x 1 = 2, x 2 = −2. 3. Логарифмическое уравнение вида log af (x) = log ag (x). Здесь a — отличное от единицы положительное число; f (x) и g (x) — элементарные алгебраические функции. Решение логарифмических уравнений такого типа сводится к решению уравнения f (x) = g (x). Поэтому для решения рассматриваемого типа уравнений log ₐf (x) = log ₐg (x) достаточно найти все решения уравнения f (x) = g (x) и среди полученных выбрать те, которые относятся к ОДЗ уравнения log ₐf (x) = g (x) log ₐ. Если уравнение f (x) = g (x) решений не имеет, то их не имеет и исходное логарифмическое уравнение. Пример: решить уравнение:ln(x + 1) = ln(2 x – 3). Решение: Находим ОДЗ: Решаем уравнение x + 1 = 2 x – 3: x = 4 є ОДЗ. Итак, решением исходного логарифмического уравнения также является это значение. Ответ: x = 4.
Отбор корней Задача 1 а) Решите уравнение:sin x = 0,5. б) Укажите корни, принадлежащие отрезку [- π; 2 π ]. Решение: а ) sin x = 0,5; х= Корни уравнения: б) Теперь будем искать корни, принадлежащие отрезку [- π; 2 π ]. Рассмотрим 3 способа отбора корней: · Способ №1. С помощью двойного неравенства: −π ≤ −1 ≤ − − Значит, n = 0, x = − π ≤ 5· −1 ≤ − − Значит, k = 0, х = 5· Этот способ наиболее точный и если учащиеся владеют навыками решения двойного неравенства, то понятный и подходит совершенно всем и в любых случаях. · Способ №2. С помощьюокружности: a) На окружности найдем края отрезка: точки – π и 2 π. б) Смотрим на точки — из каких серий решения попали в этот отрезок. в) Выбираем эти точки. Если данные отрезки бывают длиной больше 2 π, тогда можно потерять некоторые корни, поэтому рекомендуется: нарисовать вторую концентрическую окружность, будто соответствующую следующему периоду (это просто модель, которая помогает решить задачу). Этот способ хорошо дается тем, кто умеет определять на окружности точки и отсчитывать периоды.
· Способ №3. С помощьюграфика: а) Чертим график у = sin x; б) Выделяем отрезок — π; 2π; в) Проводим прямую у = г) Отмечаем точки с ординатой Способ очень наглядный и подойдет тем, кто не усвоил вышеизложенные два способа.
Показательная функция
Функцию вида f (x) = aˣ, где a > 0 и a ≠ 1, называют показательной функцией. Основные свойства показательной функции f (x) = aˣ:
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1807; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.188.166 (0.01 с.) |

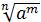 =
=  ;
; =
=  ·
· 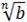 ;
; =
= 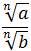 , b ≠ 0;
, b ≠ 0; =
=  ;
; ·
·  =
=  ;
; .
. =
=  =
=  .
.
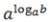 = b — основное логарифмическое тождество.
= b — основное логарифмическое тождество. = log ab − log ac — логарифм частного.
= log ab − log ac — логарифм частного. =
=  · log ab.
· log ab. .
. — переход к новому основанию.
— переход к новому основанию. =
=  · log ab.
· log ab. = b.
= b.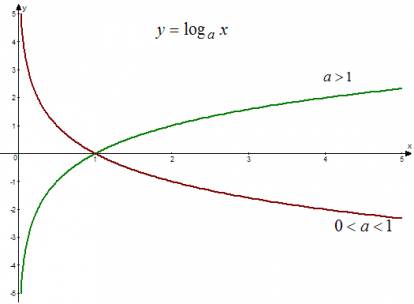
 ;
; x є R.
x є R.


 ; +∞)
; +∞) + 2 πn или x = 5·
+ 2 πn или x = 5·  Z.
Z. Z.
Z. + 2 n ≤ 2;
+ 2 n ≤ 2; ≤ 2 n ≤
≤ 2 n ≤  ;
; ≤ n ≤
≤ n ≤  .
. + 2 k ≤ 2;
+ 2 k ≤ 2; ;
;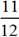 ≤ k ≤
≤ k ≤  .
. .
.
 ;
;
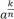 =
=  (k ϵ Z, n ϵ N);
a − x =
(k ϵ Z, n ϵ N);
a − x =  ;
ax · ay = ax+y;
;
ax · ay = ax+y;
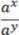 = ax−y;
(ax) y = axy;
ax · bx = (ab) x;
= ax−y;
(ax) y = axy;
ax · bx = (ab) x;
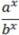 =
= 



