
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
График показательной функцииСодержание книги
Поиск на нашем сайте
Графиком показательной функции является экспонента:
Простейшие показательные уравнения Показательными называются уравнения, содержащие переменную в показателях каких-либо степеней. Для решения показательных уравнений требуется знать и уметь использовать следующую несложную теорему:
Простейшее показательное уравнение — это уравнение вида: ax = b, где а > 0, а ≠ 1. Такое уравнение не имеет корней при b ≤ 0, а при b > 0 имеет единственный корень: x = log a b. Более сложные показательные уравнения решаются по следующей схеме: · Перевести все степени к одинаковому основанию. Желательно, чтобы оно было целым и минимальным. Например, вместо 4 x лучше писать 2² ˣ, а вместо 0,01 x — вообще 10−² ˣ; · В уравнениях, где есть умножение или деление, надо выполнить эти действия. Помните: при умножении степеней с одинаковым основанием показатели складываются, при делении — вычитаются; · Если все сделано правильно, получим уравнение вида a f (x) = a g (x), где a — просто число. Его можно отбросить, поскольку показательная функция монотонна. Получим уравнение f (x) = g (x), которое легко решается. · Помните, что корни — тоже степени, но с дробным основанием:
Задача. Решите уравнение: 4 x = Решение: Итак, приведем все степени к основанию 2: 4 x = (22) x = 22 x; 1 = 20; 256 = 28. Теперь перепишем исходное уравнение и выполним деление: 4 x = Получили простейшее показательное уравнение. Отбрасываем основание — получаем: 2 x = −8 ⇒ x = −4. Ответ: −4. Задача: Решите уравнение: 92 x = Решение Снова приводим все степени к наименьшему целому основанию: 92 x = (32)2 x = 34 x; 1 = 30; 27 = 33. Обратите внимание: число 27 не является целой степенью девятки. Именно поэтому надо приводить все степени к основанию 3, а не 9. Возвращаемся к исходному уравнению: 92 x = Осталось избавиться от основания степени: 4 x = −3 ⇒ x = −3/4 = −0,75. Ответ: −0,75.
Простейшие тригонометрические уравнения Простейшими тригонометрическими уравнениями называют уравнения вида: sin x=a; cos x=a; tg x=a; ctg x=a, где a – произвольное число. Решениеуравненияsin x = a
Графическоеобоснованиерешенияуравненияsin x=a:
Частныеслучаирешенияуравненийsin x = а (неучить,анаходитьпотригонометрическомукругу)
Решениеуравненияcos x=а:
Графическоеобоснованиерешенияуравненияcos x=a
Частныеслучаирешенияуравненийcos x = а (неучить,анаходитьпотригонометрическомукругу)
Решениеуравненияtg x = а
Графическоеобоснованиерешенияуравненияtg x=a
Частныеслучаирешенияуравненийtg x=а (неучить,анаходитьпотригонометрическомукругу)
Решениеуравненияctg x=а
Графическоеобоснованиерешенияуравненияctg x = a
Частныеслучаирешенияуравненийctg x = а (неучить,анаходитьпотригонометрическомукругу)
Уравнения с модулем Определение Модуль числа а или абсолютная величина числа а равна а, если а больше или равно нулю и равна − а, если а меньше нуля: │ а │ = Из определения следует, что для любого действительного числа а, │ а │≥ 0. Геометрически │ а │означает расстояние на координатной прямой от точки, изображающей число а, до начала отсчета.
Если а ≠ 0, то на координатной прямой существует две точки а и − а, равноудаленной от нуля, модули которых равны. Если а = 0, то на координатной прямой │ а │изображается точкой 0.
Графиком функции y = │ x │ является «уголок».
I) Уравнения вида │ f (x) │ = A, A ϵ R решаются следующим образом: Если A < 0, то корней нет. Если A = 0, то уравнению │ f (x) │ = A соответствует уравнение f (x) = 0. Если A > 0, то уравнению │ f (x) │ = A соответствует равносильная совокупность:
II) Уравнения вида │ f (x)│ = g (x) решаются следующим образом: Способ №1 Уравнению │ f (x)│ = g (x) соответствует равносильная совокупность систем:
Способ №2 Уравнению │ f (x) │ = g (x) соответствует равносильная совокупность систем:
III) Уравнения вида │ f (x) │ = │ g (x) │ решаются следующим образом: Способ №1 Уравнению │ f (x) │ = │ g (x) │ соответствует равносильное уравнение f 2 (x) = g 2 (x). Способ №2 Уравнению │ f (x)│ = │ g (x) │ соответствует равносильная совокупность:
IV) Уравнения вида │ f (x) │ = − f (x) и │ f (x) │ = f (x) решаются следующим образом: Уравнению │ f (x) │ = − f (x) соответствует равносильное неравенство f (x) ≤ 0. Уравнению │ f (x) │ = f (x) соответствует равносильное неравенство f (x) ≥ 0. V) Общая схема решения уравнений содержащих знак модуль. Например: │ x 2 − 1│ + │ x 2 − 4│ = 3. Найдем нули выражений, стоящих под знаком модуль. x = ±1, x = ±2. И раскроем модуль на каждом из 5 промежутков, на которые оказалась разделена числовая ось числами x = ±1, x = ±2. I) (−∞; −2] — промежуток, значит в ответ попадает только решение x = −2. II) В ответ будет входить весь промежуток. III) Оба решения попадают в рассматриваемый промежуток. IV) В ответ будет входить весь промежуток. V) [2; +∞) — промежуток, т. е. подходит решение x = 2. Ответ: [−2; −1]
Формулы тригонометрии
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 717; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.139.31 (0.009 с.) |



 =
=  ;
;  =
=  ;
;  =
=  =
= 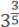 .
. .
. 22 x =
22 x = 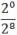
 .
.
 [-1;1],
уравнение решений не имеет
[-1;1],
уравнение решений не имеет

 + 2 πn, n є Z
+ 2 πn, n є Z


 + 2 πn, n є Z
x 2=
+ 2 πn, n є Z
x 2= 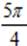 + 2 πn, n є Z
+ 2 πn, n є Z
 + 2 πn, n є Z
+ 2 πn, n є Z

 + πn, n є Z
+ πn, n є Z
 + 2 πn, n є Z
x 2 =
+ 2 πn, n є Z
x 2 = 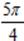 + 2 πn, n є Z
+ 2 πn, n є Z
 + 2 πn, n є Z
+ 2 πn, n є Z







 ⇔
⇔ 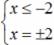
 ⇔
⇔ 
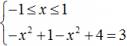 ⇔
⇔ 
 ⇔
⇔ 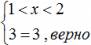
 ⇔
⇔ 
 [1; 2].
[1; 2].


