
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дробно-рациональное уравнениеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Уравнение называется дробно-рациональным, если в этом уравнении есть деление на выражение, содержащее переменную x. Замечание: сравните с примером 2 в линейных уравнениях, где в знаменателях только числа. Примеры дробно-рационального уравнения: x +
Дробно- рациональные уравнения обычно решаются следующим образом: · определяем значения переменных, при которых любой из знаменателей обращается в ноль, другими словами, находим область допустимых значений уравнения (ОДЗ); · находим общий знаменатель дробей и умножаем на него обе части уравнения; · решаем получившееся уравнение; · исключаем из его корней те, которые обращают в ноль общий знаменатель дробей, т. е. не подходят по ОДЗ. Пример: Решить дробно-рациональное уравнение: При значениях x = 0, x = 5 получаем деление на ноль, чего быть не может, значит, эти числа не могут быть ответом в данной задаче, т. е. не входят в ОДЗ. Находим общий знаменатель ― это x (x – 5). Домножим на него обе части уравнения:
Сделаем преобразования и решим получившееся уравнение: x (x – 3) + (x – 5) + x + 5; x 2 – 3 x + x – 5 = x + 5; x 2 – 3 x + x – 5 – x – 5 = 0; x 2 – 3 x – 10 = 0. Решите это квадратное уравнение сами. Корни получаются: –2 и 5. Проверим, являются ли эти числа корнями исходного уравнения. При x = –2 общий знаменатель x (x – 5) не обращается в нуль. Значит, –2 является корнем исходного уравнения. При x = 5 общий знаменатель обращается в нуль, и два выражения из трех теряют смысл. Значит, число 5 не является корнем исходного уравнения. Ответ: –2. Замечание: после нахождения корня уравнения, его всегда можно подставить в исходное уравнение и получить верное равенство. Проделайте это для всех рассмотренных примеров.
Стeпени Этот урок посвящен степеням и корням. Вначале мы обсудим понятия степень и кореньи как с ними работать. Далее рассмотрим ряд свойств, на знании которых, в основном, и базируется правильная работа с заданиями из этой темы. Ну и конечно, для лучшего понимания, подкрепим все примерами. Выражение an называется степенью. В этом выражении число a называется основанием степени, а число n ― показателем степени. Например, степень 35, имеет основание степени равное 3, а показатель степени равен 5. Это число можно получить, если мы умножим число 3 само на себе 5 раз, т. е. 35 = 3 ∙ 3 ∙ 3 ∙ 3 ∙ 3. Для положительных чисел a и b и чисел n и m справедливы следующие свойства степени: 1) a 0 = 1. Любое число в нулевой степени равно 1. 2) a 1 = a. Степенью числа с показателем 1 называется само это число. 3) an ∙ am = an+m. При умножении степеней с одинаковыми основаниями, основание остается прежним, а показатели складываются. 4) При делении степеней с одинаковыми основаниями, основание остается прежним, а показатели вычитаются. 5) (ab) n = an ∙ bn. При возведении в степень произведения, в эту степень возводится каждый множитель. 6) При возведении в степень дроби в эту степень возводится числитель дроби и знаменатель. 7) (an) m = an∙m. При возведении степени в степень показатели перемножаются. 8) a-n = При возведении в отрицательную степень, основание степени «переворачивается», и знак показателя степени меняется на противоположный. Пример 1: Применим свойство 3.
Пример 2: Применим свойство 6.
Пример 3: Применим свойство 8. 4-2 =
Кoрни Корнем n -ой степени n√a из числа a называется число, n -я степень которого равна a. Натуральное число n называется показателем корня. Число a называется подкоренным выражением. Замечание: степень корня ― это натуральное число, большее 1. Корень второй степени √a называется квадратным корнем и двойка обычно опускается. Корень третьей степени 3 √a называется кубическим корнем. Выделяют корни четной степени (n ― четное) и корни нечетной степени (n ― нечетное): · Корень нечетной степени из положительного числа ― обязательно положительноечисло. n√a = b, где a, b > 0, n ― нечетное. Пример: 3√8 = 2, 5√32 = 2, 12√1 = 1. · Корень нечётной степени из отрицательного числа ― отрицательное число, однозначно определенное. n√a = b, где a, b < 0, n ― нечетное. Пример: 3√–8 = –2, 5√–243 = –3, 9√–1 = –1. · Корень чётной степени берется только из положительного числа. n√a = b, где a, b > 0, n ― четное; n√a не существует, если а < 0, n ― четное. Пример: √16 = 4, 4√81 = 3, 14√1 = 1. Для положительных чисел a и b и чисел n и m справедливы следующие свойства корня: 1) n√an = a; 2) n√a ∙ n√b = n√ab; 3) 4) n√am = (n√a) m; 5) 6) n√am = am/n. Замечание: шестое свойство показывает, что на самом деле корень любой степени ―это не что иное как степень числа, работу с которыми мы обсуждали в первой части этого урока. Значит, залог успешной работы в теме «корни» полностью основывается на правильной работе в теме «степени». Для корня четной степени (n ― четное) справедливы ещё ряд свойств (a, b ― любые числа): 1) n√an = a; 2) n√ab = 3) Пример 1: Применим свойство 1 и 2. 3√2 ∙ 3√32 = 3√64 = 3√43 = 4. Пример 2: Применим свойство 3.
Пример 3: Применим свойство 4 и 6. 43/2 = √43 = (√4)3 = 23 = 8. Мы рассмотрели две, в общем-то, технические темы и познакомились не только с понятиями, которые здесь используются, но и с основными свойствами степеней и корней, необходимыми для решения задач. На этом можно поставить запятую в освоении этих тем, а для того чтобы она стала точкой, необходимо закрепить навыки работы со степенями и корнями на упражнениях, которые мы вам подготовили.
Введение в стереометрию Стереометрией называют раздел геометрии, в котором изучают свойства пространственных фигур. Простейшими фигурами в пространстве являются точка, прямая и плоскость.
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 782; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.86.58 (0.008 с.) |

 = 5 x – 17;
= 5 x – 17; +
+  = 5.
= 5. +
+  =
=  .
. = an-m.
= an-m. =
=  .
. =
=  .
. = 35-3 = 32 = 9.
= 35-3 = 32 = 9. =
= 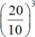 = 23 = 8.
= 23 = 8.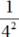 =
=  .
. =
=  ;
; = nm√a;
= nm√a; ∙
∙  ;
; =
=  .
. =
=  =
=  =
=  =
=  .
.


